2.2. Propriétés de l’onde : vitesse, amplitude, fréquence et période

Caractéristiques d’onde

Dans ce chapitre, nous allons définir quelques notion qui permettent de décrire une onde :

Caractéristiques d’une onde

Une onde mécanique est définie par sa :

Fréquence \(f\) :

La fréquence \(f\) est le nombre d’ondes passant par un point spécifique par seconde.
Elle se mesure en inverse de seconde (\(\text{s}^{-1}\)) ou en Hertz (\(\text{Hz}\))

Période \(T\) :

La période \(T\) d’une d’une onde est le temps nécessaire à la réalisation d’un cycle d’onde périodique.
Elle se mesure en seconde (\(\text{s}\))

Longueur d’onde \(\lambda\) :

La longueur d’onde \(\lambda\) est la distance entre deux parties identiques adjacentes d’une onde (par exemple, deux sommets successifs de l’onde), parallèle à la direction de propagation.
Elle se mesure en mètre (\(\text{m}\))

Vitesse d’onde \(v_{w}\) :

La vitesse de l’onde \(v_{w}\) est la vitesse à laquelle la perturbation se déplace.
Elle se mesure en mètre par seconde (\(\text{m/s}\))

Amplitude \(A\) :

L’amplitude \(A\) d’une onde est la distance entre la position de repos et le déplacement maximal de l’onde.
Elle se mesure en mètre (\(\text{m}\))
L’amplitude n’est pas vraiment une grandeur importante pour comprendre les ondes mécaniques.

Conseils pour réussir

La vitesse des vagues est parfois aussi appelée vitesse de propagation (ou célérité) car la perturbation se propage d’un endroit à un autre.

Vitesse d’une onde.

Comme une onde se propage, on peut lui associer une vitesse.

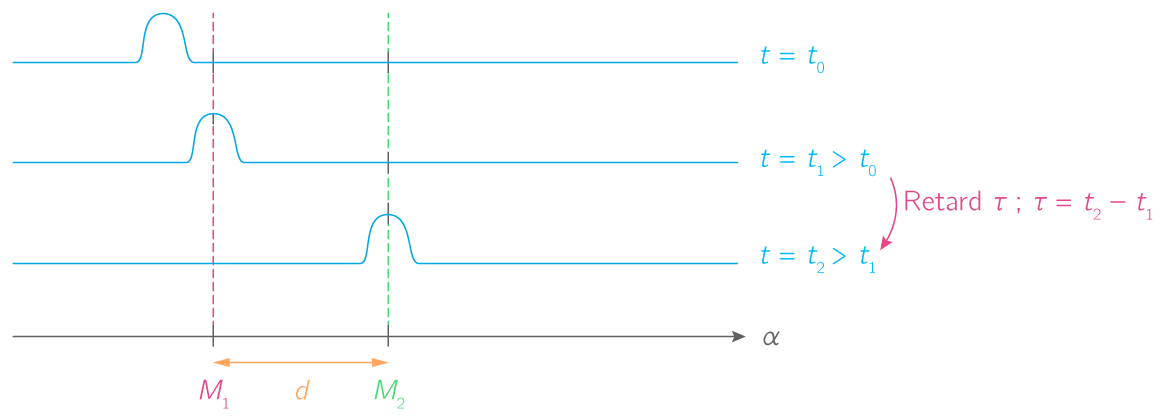
Fig. 2.9 L’impulsion s’est déplacée d’une distance \(d\) (de \(M_{1}\) à \(M_{2}\)) pendant un temps \(\tau\) (de \(t_{1}\) à \(t_{2}\)).

Vitesse \(v_w\) d’une onde

La vitesse de propagation d’une onde est le rapport entre la distance \(d\) parcourue par la perturbation et la durée écoulée \(t\). Elle se mesure en mètre par seconde \((\text{m/s})\)

(2.1)\[v_w=\dfrac{d}{t}\]

avec \(d\) en mètre et \(t\) en seconde.

Exemple

Une onde parcourt \(10\,m\) en \(25\,s\).
Quelle est sa vitesse ?

solution

On a \(d=10\,m\) et \(t=25\,s\), donc :

\[v_w=\dfrac{d}{t}=\dfrac{10}{25}=0.4\,m/s\]

La force de tension \(F_T\) d’une corde tendue, joue également un rôle dans la vitesse de propagation : on observe que plus une corde est tendue, plus la vitesse de propagation des ondes est grande. Des mesures expérimentales nous montrent que le carré de la vitesse de propagation \(v_w\) d’une onde dans une corde est :

• proportionnel à la force de tension \(F_T\) de la corde ;

• inversement proportionnel à la masse linéaire \(\mu\) de la corde. Ces propriétés se traduisent par la relation algébrique :

(2.2)\[v_w=\sqrt{\dfrac{F_{T}}{\mu}}\]

ou :

• \(v\) est la vitesse de propagation en \((\text{m/s})\)

• \(F_T\) la force de tension de la corde en \((\text{N})\)

• \(\mu\) la masse linéaire de la corde en \((\text{kg/m})\)

Exemple

Une corde de \(3\,m\), pesant \(1.5\,kg\), est tendue avec une force de tension de \(25\,kN\).

1. Quelle est la vitesse de l’onde dans cette corde ?

2. On double la tension, comment varie la vitesse de l’onde ?

solution

1. Une corde de \(3\,m\) avec une masse de \(1.5\,kg\) donne une masse linéaire de :

\[\mu=\dfrac{1.5}{3}=0.5\,kg/m\]

Ce qui nous donne une vitesse de :

\[v_w=\sqrt{\dfrac{F_{T}}{\mu}}=\sqrt{\dfrac{25'000\,N}{0.5}}=\sqrt{50'000}=223.6\,m/s\]

3. Si on double la tension, la vitesse est multipliée par \(\sqrt{2}\) :

\[\begin{split}v_w=\sqrt{\dfrac{F_{T}}{\mu}}=\sqrt{\dfrac{50'000\,N}{0.5}}=\sqrt{100'000}=316.2\,m/s\\ \sqrt{2}\cdot 223.6=316.2\,m/s\end{split}\]

Période et fréquence

Les ondes périodiques correspondent à des phénomènes qui se répètent périodiquement. Ces ondes sont caractérisées par une période \(T\) et par une fréquence \(f\).

Période

La période \(T\) d’une onde progressive périodique est le temps le plus court au bout duquel un point se retrouve dans le même état vibratoire. La période \(T\) se mesure en secondes \((\text{s})\).

La période correspond au temps qu’il y a entre deux répétions d’un signal périodique. La période du mouvement de l’aiguille des secondes d’une montre est \(T=60\,\text{s}\), car elle revient au même endroit toutes les \(60\,\text{s}\). En astronomie, la période de révolution désigne l’intervalle de temps entre deux passages consécutifs d’un astre en un point quelconque de son orbite. La période de rotation correspond à la durée nécessaire à un astre pour faire un tour sur lui-même.

La période d’une onde périodique peut être déterminée graphiquement : elle correspond à la durée du motif élémentaire (Fig. 2.10).

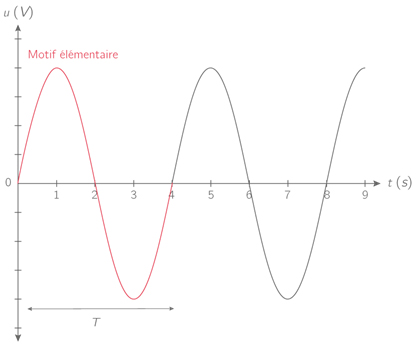
Fig. 2.10 La période de ce signal périodique vaut \(T=4.0\,\text{s}\)

Pour caractériser une onde progressive périodique, on utilise souvent la fréquence au lieu de la période.

Fréquence

Par définition, la fréquence temporelle \(f\), exprimée en Hertz \(\text{Hz}\), est l’inverse de la période \(T\), exprimée en secondes \(\text{s}\)

\[f=\dfrac{1}{T}\]

Dans cette relation, la période doit obligatoirement être exprimée en secondes. Le Hertz est l’inverse de la seconde : \(1\,\text{Hz}=1\,\text{s}^{-1}\)

La fréquence correspond au nombre de répétition d’un signal périodique pendant \(1\) seconde.

Exemple

Un capteur piezoélectrique vibre 40 mille fois par seconde.
Quelle est la période et la fréquence de l’onde (ultra-son) émise par ce capteur ?

solution

La période \(T\) de l’onde ultra-sonore émise par ce capteur piezoélectrique correspond au temps entre \(2\) vibration. On a donc :

\[T=\dfrac{1}{40´000}=0.000025\,s=25\cdot 10^{-6}\,s=25\,\mu s\]

La fréquence \(f\) du signal est donc de :

\[f=\dfrac{1}{T}=\dfrac{1}{25\cdot 10^{-6}}=40'000\,Hz=4\cdot 10^{4}\,Hz\]

On remarque que la fréquence était directement mentionnée dans la donnée par le vibre 40 mille fois par seconde.

Longueur d’onde et amplitude

La longueur d’onde est la période spatiale d’une onde, c’est-à-dire la plus petite distance séparant deux points dans le même état. Les ondes progressives périodiques étant des perturbations se propageant de façon périodique, on peut, à un instant figé (photo), définir une périodicité spatiale en plus de la périodicité temporelle :

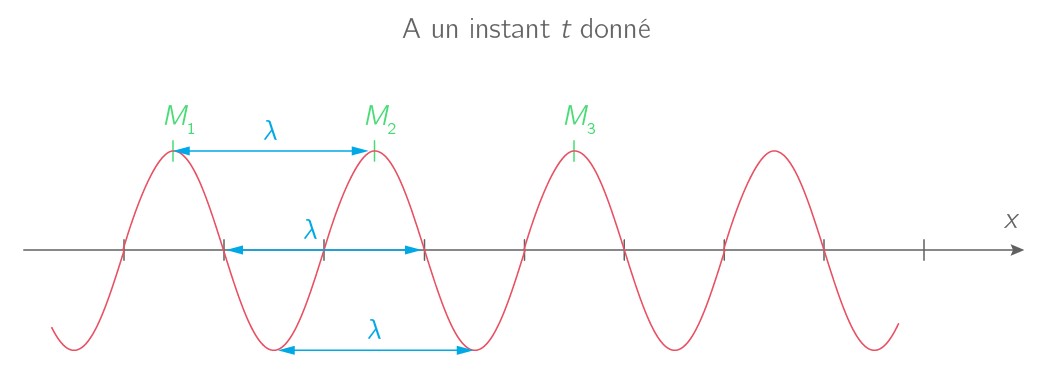
Fig. 2.11 Définition de la longueur d’onde \(\lambda\).

Tout comme la périodicité temporelle est mesurée par la période \(T\), la périodicité spatiale est mesurée par longueur d’onde \(\lambda\) (Fig. 2.11).

Longueur d’onde

La longueur d’onde \(\lambda\) est la distance la plus courte qui sépare deux points dans le même état vibratoire à un instant \(t\) et son unité est le mètre (\(\text{m}\)). On dit que ces deux points vibrent en phase.

Considérons la vague d’eau périodique dans Fig. 2.12. Sa longueur d’onde \(\lambda\) est la distance d’une crête à l’autre ou d’un creux à l’autre. La longueur d’onde peut également être considérée comme la distance parcourue par une onde après un cycle complet - ou une période \(T\). Le temps d’un mouvement complet de haut en bas est également la période \(T\) de la vague. Sur la figure, l’onde elle-même se déplace vers la droite avec une vitesse d’onde \(v_{w}\). Son amplitude \(A\) est la distance entre la position de repos et le déplacement maximal - soit la crête ou le creux - de la vague. Il est important de noter que ce mouvement de la vague est en fait la perturbation qui se déplace vers la droite, et non l’eau elle-même ; sinon, la mouette se déplacerait aussi vers la droite. Au lieu de cela, la mouette se déplace uniquement de haut en bas sur place au fur et à mesure que les vagues passent en dessous, parcourant une distance totale de \(2A\) en un cycle. Cependant, comme mentionné dans le texte sur le surf, les vagues réelles de l’océan sont plus complexes que cet exemple simplifié.

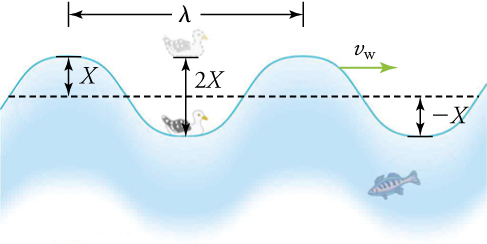
Fig. 2.12 L’onde a une longueur d’onde \(\lambda\), qui est la distance entre deux crêtes de l’onde. La perturbation verticale, de haut en bas, de la surface se déplace parallèlement à la surface avec une vitesse \(v_w\).

Remarque

La crête d’une vague est parfois aussi appelée le pic.

Question

Si vous êtes sur un bateau dans le creux d’une vague sur l’océan, et que l’amplitude de la vague est de \(1\,\text{m}\), quelle est la hauteur de la vague à partir de votre position ?

1. \(1\,\text{m}\)

2. \(2\,\text{m}\)

3. \(4\,\text{m}\)

4. \(8\,\text{m}\)

réponse

Réponse 2. : \(2\,\text{m}\)

L’amplitude est la distance entre la position de repos et le déplacement maximal de la vague. Comme vous vous trouvez dans le creux de la vague, vous êtes à une position de \(-1\,\text{m}\) par rapport à la position de repos (négatif, car vous êtes sous la position de repos). Le sommet de la vague, qui est \(1\,\text{m}\) au-dessus de la position de repos de la vague, se trouve donc à une distance de \(1\,\text{m}+1\,\text{m}=2\,\text{m}\) de vous.

YouTube

Cette vidéo est la suite de la vidéo Introduction aux vagues de la section Types d’ondes. Il traite des propriétés d’une onde périodique : amplitude, période, fréquence, longueur d’onde et vitesse d’onde.

Relation fondamentale

Il est possible de trouver une relation entre la fréquence, la période, la vitesse et la longueur d’une onde.

On rappel que fréquence est le nombre d’ondes par seconde, et que la période est la durée (le nombre de secondes) pour une onde, la relation entre la fréquence et la période est

\[f = \frac{1}{T}\]

ou

\[T = \frac{1}{f}\]

Nous pouvons voir à partir de cette relation qu’une fréquence plus élevée signifie une période plus courte. Rappelez-vous que l’unité de fréquence est le hertz (\(\text{Hz}\)) et que \(1\text{Hz}\) correspond à un cycle - ou une onde - par seconde.

La vitesse de propagation \(v_{w}\) est la distance parcourue par l’onde dans un temps donné (\(v=\frac{d}{t}\)). Dans le cas d’une onde périodique, on sait qu’elle parcourt une distance égale à sa longueur d’onde \(\lambda\) dans un temps équivalent à une période \(T\). Sous forme d’équation, on obtient :

Relation fondamentale

La relation fondamentale d’une onde, relie sa vitesse de propagation \(v_w\) avec sa longueur d’onde \(\lambda\), sa fréquence \(f\) et sa période \(T\) :

\[v_{w} = \dfrac{\lambda}{T}\]

ou

\[v_{w} = \lambda\cdot f\]

À partir de cette relation, nous voyons que dans un milieu où \(v_{w}\) est constant, plus la fréquence est élevée, plus la longueur d’onde est petite - voir la Fig. 2.13.

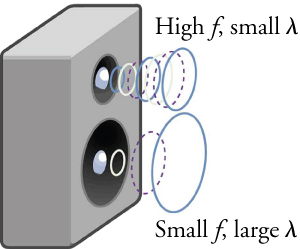
Fig. 2.13 Parce qu’ils se déplacent à la même vitesse dans un milieu donné, les sons à basse fréquence doivent avoir une longueur d’onde plus grande que les sons à haute fréquence. Ici, les sons de basse fréquence sont émis par le grand haut-parleur, appelé woofer, tandis que les sons de haute fréquence sont émis par le petit haut-parleur, appelé tweeter.

Ces relations fondamentales sont vraies pour tous les types d’ondes. Par exemple, pour les vagues d’eau, \(v_{w}\) est la vitesse d’une onde de surface ; pour le son, \(v_{w}\) est la vitesse du son ; Et pour la lumière visible, \(v_{w}\) est la vitesse de la lumière. L’amplitude \(A\) est complètement indépendante de la vitesse de propagation \(v_{w}\) et ne dépend que de la quantité d’énergie dans l’onde.

Exemple

Pour produire la note La, la membrane d’un haut parleur bat \(440\) fois par seconde.
La vitesse du son est de \(340\,\text{m/s}\).

1. Quelle est la fréquence de cette onde sonore ?

2. Quelle est la période de cette onde sonore ?

3. Quelle est la longueur d’onde de cette note ?

solution

1. \(440\) fois par seconde donne une fréquence de : \(f=440\,\text{Hz}\)

2. \(T=\dfrac{1}{f}=0.00227\,\text{s}=2.27\,\text{ms}\)

3. \(\lambda=\frac{v}{f}=\frac{340}{440}=0.773\,\text{m})77.3\,\text{cm}\)

Géologie : Physique des ondes sismiques

Fig. 2.14 L’effet destructeur d’un tremblement de terre est une preuve palpable de l’énergie transportée par les ondes sismiques. L’évaluation des tremblements de terre sur l’échelle de Richter est liée à la fois à leur amplitude et à l’énergie qu’ils transportent. (Maître de 2e classe Candice Villarreal, U.S. Navy)

Les géologues s’appuient fortement sur la physique pour étudier les tremblements de terre, car les tremblements de terre impliquent plusieurs types de perturbations des vagues, notamment la perturbation de la surface de la Terre et les perturbations de la pression sous la surface. Les ondes sismiques de surface sont similaires aux ondes de surface sur l’eau. Les ondes sous la surface de la Terre ont à la fois des composantes longitudinales et transversales. Les ondes longitudinales d’un tremblement de terre sont appelées ondes de pression (ondes \(\text{P}\)) et les ondes transversales sont appelées ondes de cisaillement (ondes \(\text{S}\)). Ces deux types d’ondes se propagent à des vitesses différentes, et la vitesse à laquelle elles se déplacent dépend de la rigidité du milieu dans lequel elles se déplacent. Pendant les tremblements de terre, la vitesse des ondes \(\text{P}\) dans le granit est significativement plus élevée que la vitesse des ondes \(\text{S}\). Les deux composantes des tremblements de terre se déplacent plus lentement dans des matériaux moins rigides, tels que les sédiments. Les ondes \(\text{P}\) ont des vitesses de \(4\) à \(7\,\text{km/s}\) et les ondes \(\text{S}\) ont des vitesses de \(2\) à \(5\,\text{km/s}\), mais les deux sont plus rapides dans des matériaux plus rigides. L’onde \(\text{P}\) s’éloigne progressivement de l’onde \(\text{S}\) au fur et à mesure qu’elle traverse la croûte terrestre. Pour cette raison, la différence de temps entre les ondes \(\text{P}\) et \(\text{S}\) est utilisée pour déterminer la distance à leur source, l’épicentre du tremblement de terre.

Nous savons, grâce aux ondes sismiques produites par les tremblements de terre, que certaines parties de l’intérieur de la Terre sont liquides. Les ondes de cisaillement ou transversales ne peuvent pas traverser un liquide et ne sont pas transmises par le noyau de la Terre. En revanche, les ondes de compression ou longitudinales peuvent traverser un liquide et elles traversent le noyau.

Toutes les ondes transportent de l’énergie, et l’énergie des ondes sismiques est facile à observer en fonction de la quantité de dommages laissés après que le sol a cessé de bouger. Les tremblements de terre peuvent faire trembler des villes entières, effectuant le travail de milliers de boules de démolition. La quantité d’énergie dans une onde est liée à son amplitude. Les tremblements de terre de grande amplitude produisent de grands déplacements de sol et des dommages plus importants. Au fur et à mesure que les ondes sismiques se propagent, leur amplitude diminue, de sorte qu’il y a moins de dommages à mesure qu’elles s’éloignent de la source.

Vérifiez votre compréhension

Quelle est la relation entre la vitesse de propagation, la fréquence et la longueur d’onde des ondes \(\text{S}\) lors d’un tremblement de terre ?

1. La relation entre la vitesse de propagation, la fréquence et la longueur d’onde est \(v_{\text{w}} = \lambda\cdot f\)

2. La relation entre la vitesse de propagation, la fréquence et la longueur d’onde est \(v_{\text{w}} = \frac{f}{\lambda}.\)

3. La relation entre la vitesse de propagation, la fréquence et la longueur d’onde est \(v_{\text{w}} = \frac{\lambda}{f}.\)

4. La relation entre la vitesse de propagation, la fréquence et la longueur d’onde est \(v_{\text{w}} = \sqrt{\lambda\cdot f}.\)

solution

Réponse 1. La relation entre la vitesse de propagation, la fréquence et la longueur d’onde est \(v_{\text{w}} = \lambda\cdot f\)

PhET simulation

Corde vibrante

Dans cette animation, regardez comment une corde vibre au ralenti en choisissant le réglage Ralenti. Sélectionnez les options Pas d'extrémité et Manuel, et faites bouger l’extrémité de la ficelle avec la souris pour faire des vagues vous-même. Passez ensuite au réglage Osciller pour générer automatiquement des ondes. Ajustez la Fréquence et l’Amplitude des oscillations pour voir ce qui se passe. Expérimentez ensuite le réglage de l’Amortissement et de la Tension.

Vérifiez votre compréhension

Lequel des paramètres - amplitude, fréquence, amortissement ou tension - modifie l’amplitude de l’onde lorsqu’elle se propage ? Qu’est-ce que cela fait à l’amplitude ?

1. La fréquence diminue l’amplitude de l’onde au fur et à mesure qu’elle se propage.

2. La fréquence augmente l’amplitude de l’onde au fur et à mesure qu’elle se propage.

3. L’amortissement diminue l’amplitude de l’onde au fur et à mesure qu’elle se propage.

4. L’amortissement augmente l’amplitude de l’onde au fur et à mesure qu’elle se propage.

solution

Réponse 3. L’amortissement diminue l’amplitude de l’onde au fur et à mesure qu’elle se propage.

Exemples

Calculer la vitesse de propagation des vagues : Mouette dans l’océan

Calculez la vitesse des vagues de l’océan dans la figure Fig. 2.12 si la distance entre les crêtes des vagues est de \(10.0\,\text{m}\) et que le temps nécessaire à une mouette pour monter et descendre est de \(5.00\,\text{s}\)

stratégie

Les valeurs de la longueur d’onde : \(\lambda = 10.0\,\text{m}\) et la période \(\text{T} = 5.00\,\text{s}\) sont données et on nous demande de trouver \(v_{w}\) Par conséquent, nous pouvons utiliser \(v_{w} = \frac{\lambda}{T}\) pour trouver la vitesse de l’onde.

solution

Entrez les valeurs connues dans \(v_{w} = \frac{\lambda}{T}\) :

\[v_{w} = \frac{10.0\,\text{m}}{5.00\,\text{s}} = 2.00\,\text{m/s}\]

discussion

Cette vitesse lente semble raisonnable pour une vague océanique. Notez que dans la figure, la vague se déplace vers la droite à cette vitesse, ce qui est différent de la vitesse variable à laquelle la mouette se déplace de haut en bas.

Calculer la période et la vitesse d’onde d’un ressort jouet

La femme de la Fig. 2.5 crée deux vagues par seconde en secouant le ressort du jouet de haut en bas.

1. Quelle est la période de chaque vague ?

2. Si chaque onde se déplace de \(0.9\) mètre après un cycle complet d’onde, quelle est la vitesse de propagation de l’onde ?

stratégie

Stratégie pour 1.

Pour trouver la période, nous résolvons \(T = \frac{1}{f}\), étant donné la valeur de la fréquence \(f = 2\,\text{Hz}\)

Stratégie pour 2.

Étant donné qu’une définition de la longueur d’onde est la distance parcourue par une onde après un cycle complet - ou une période - les valeurs de la longueur d’onde (\(\lambda = 0.9\,\text{m}\)) ainsi que la fréquence sont données. Par conséquent, nous pouvons utiliser \(v_{w} = \lambda\cdot f\) pour trouver la vitesse de l’onde.

solution

Solution pour 1.

Entrez la valeur connue dans \(T = \frac{1}{f}\)

\[T = \dfrac{1}{2\,\text{Hz}} = 0.5\,\text{s}\]

Solution pour 2.

Entrez les valeurs connues dans \(v_{w} = \lambda\cdot f\)

\[v_{w} = \lambda\cdot f = (0.9\,\text{m})(2\,\text{Hz}) = 1.8\,\text{m/s}\]

discussion

Nous aurions également pu utiliser l’équation \(v_{\text{w}} = \frac{\lambda}{T}\) pour résoudre la vitesse de l’onde, puisque nous connaissons déjà la valeur de la période \(\text{T} = 0.5\,\text{s}\) à partir de notre calcul dans la partie 1, et nous aurions obtenu la même réponse.

Exercices

Exercice 1

La fréquence d’une onde est de \(10\,\text{Hz}\). Quelle est sa période ?

1. La période de l’onde est de \(100\,\text{s}\)

2. La période de l’onde est de \(10\,\text{s}\)

3. La période de l’onde est de \(0.01\,\text{s}\)

4. La période de l’onde est de \(0.1\,\text{s}\)

solution

Réponse 4. la période de l’onde est de \(0.1\,\text{s}\)

\(T=\dfrac{1}{f}=\dfrac{1}{10}=0.1\,\text{s}\)

Exercice 2

Quelle est la vitesse d’une onde dont la longueur d’onde est de \(2\,\text{m}\) et dont la fréquence est de \(5\,\text{Hz}\) ?

1. La vitesse est de \(20\,\text{m/s}\)

2. La vitesse est de \(2.5\,\text{m/s}\)

3. La vitesse est de \(0.4\,\text{m/s}\)

4. La vitesse est de \(10\,\text{m/s}\)

solution

Réponse 4. la vitesse est de \(10\,\text{m/s}\)

\(v=\lambda\cdot f=2\cdot 5=10\,\text{m/s}\)

Vérifiez votre compréhension

Questions 1

Quelle est l’amplitude d’une onde ?

1. Un quart de la hauteur totale de la vague

2. La moitié de la hauteur totale de la vague

3. Deux fois la hauteur totale de la vague

4. Quatre fois la hauteur totale de la vague

réponse

Réponse 2. La moitié de la hauteur totale de la vague

Questions 2

Qu’entend-on par la longueur d’onde d’une onde ?

1. La longueur d’onde est la distance entre les parties identiques adjacentes d’une onde, parallèle à la direction de propagation.

2. La longueur d’onde est la distance entre les parties identiques adjacentes d’une onde, perpendiculaire à la direction de propagation.

3. La longueur d’onde est la distance entre une crête et le creux adjacent d’une onde, parallèle à la direction de propagation.

4. La longueur d’onde est la distance entre une crête et le creux adjacent d’une onde, perpendiculaire à la direction de propagation.

réponse

Réponse 1. La longueur d’onde est la distance entre les parties identiques adjacentes d’une onde, parallèle à la direction de propagation.

Questions 3

Comment pouvez-vous exprimer mathématiquement la fréquence des ondes en termes de période d’onde ?

1. \(f = \frac{1}{T}\)

2. \(f = \left(\frac{1}{T}\right)^{2}\)

3. \(\text{f} = \text{T}\)

4. \(f = \left(T\right)^{2}\)

réponse

Réponse 1. \(f = \frac{1}{T}\)

Questions 4

Quand la longueur d’onde est-elle directement proportionnelle à la période d’une onde ?

1. Lorsque la vitesse de l’onde est réduite de moitié

2. Lorsque la vitesse de l’onde est constante

3. Lorsque la vitesse de l’onde est doublée

4. Lorsque la vitesse de l’onde est triplée

réponse

Réponse 2. Lorsque la vitesse de l’onde est constante (\(v=\frac{\lambda}{T}\))

YouTube

Quelques liens de vidéo utiles sur le même sujet :

1. ONDE MÉCANIQUE 👉 Célérité et retard

2. Calculer la célérité d’une onde mécanique