3.2. Intensité et niveau sonore#
Intensité d’une onde sonore#

Fig. 3.8 Le bruit sur les routes bondées comme celle-ci à Delhi fait qu’il est difficile d’entendre les autres, à moins qu’ils ne crient. (crédit :Lingaraj G J, Flickr)*#
Alerte aux idées fausses
Bien que l’intensité sonore soit proportionnelle à l’amplitude, il s’agit de grandeurs physiques différentes. L’intensité sonore est définie comme la puissance acoustique par unité de surface, tandis que l’amplitude est la distance entre la position de repos et la crête d’une vague.
Dans une forêt tranquille, on peut parfois entendre une seule feuille tomber au sol. Mais dans un embouteillage rempli de voitures qui klaxonnent, vous devrez peut-être crier juste pour que la personne à côté de vous puisse entendre Fig. 3.8.
L’intensité d’un son est liée à l’énergie de vibration de sa source. Dans les dessins animés, le caricaturiste montre souvent une bouche grande ouverte avec une luette vibrante (le tissu suspendu à l’arrière de la bouche) pour représenter un son fort provenant de la gorge. La Fig. 3.9 montre une telle représentation caricaturale d’un oiseau exprimant bruyamment son opinion.
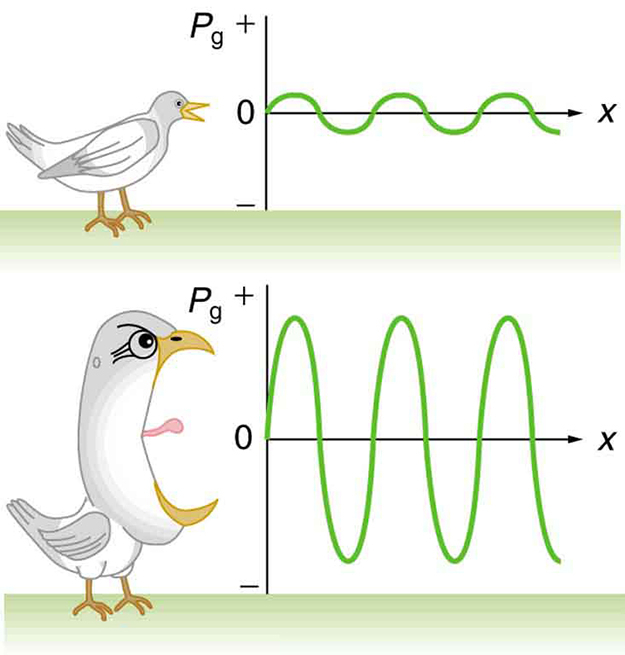
Fig. 3.9 Graphiques des pressions dans deux ondes sonores d’intensités différentes. Le son le plus intense est produit par une source qui a des oscillations de plus grande amplitude et a des maxima et des minima de pression plus élevés. Parce que les pressions sont plus élevées dans le son de plus grande intensité, il peut exercer des forces plus importantes sur les objets qu’il rencontre.#
L’intensité sonore, notée \(\boldsymbol{I}\), d’une onde sonore correspond à l’énergie transportée par cette onde par unité de surface et par unité de temps. Elle s’exprime en watts par mètre carré (\([W\cdot [m^{-2}]\)). Il s’agit donc d’une puissance par mètre carré. Sous forme d’équation, l’intensité \(I\) est :
où \(P\) est la puissance à travers une zone \(A\). L’unité SI pour \(I\) est le watt par mètre carré \([W/m^2]\). L’intensité d’un son dépend de son amplitude de pression.
Niveau sonore#
Vous avez peut-être remarqué que lorsque les gens parlent de l’intensité d’un son, ils le décrivent en décibels plutôt qu’en watts par mètre carré. Alors que l’intensité sonore (en \(W/m^2\)) est l’unité SI, le niveau d’intensité sonore en décibels (\(dB\)) est plus pertinent pour la façon dont les humains perçoivent les sons. La façon dont nos oreilles perçoivent le son peut être décrite plus précisément par le logarithme de l’intensité d’un son plutôt que par l’intensité d’un son directement. Le niveau d’intensité sonore \(\beta\) est défini comme étant
L’échelle des décibels
Le niveau sonore \(\beta\) d’une source est défini par la relation suivante :
où :
\(I\) est l’intensité sonore en watts par mètre carré (\(W/m^2\))
\(I_0 = 10^{-12}\,W/m^2\) est une intensité de référence.
\(I_0\) est choisi comme point de référence car il s’agit de l’intensité sonore la plus faible qu’une personne ayant une audition normale peut percevoir.
Le niveau de décibels d’un son d’une intensité de \(10^{-12}\,W/m^2\) est \(\beta= 0\,dB\) car \(\text{~log}_{10}\,1=0\). C’est-à-dire que le seuil de l’audition humaine est de \(0\) décibel.
Chaque facteur d’intensité de \(10\) correspond à \(10\,dB\). Par exemple, un son de \(90\,dB\) par rapport à un son de \(60\,dB\) est \(30\,dB\) plus élevé, soit trois facteurs de \(10\) (c’est-à-dire \(10^3\) fois) plus intense. Un autre exemple est que si un son est \(10^7\) plus intense qu’un autre, il est \(70\,dB\) plus élevé.
Puisque \(\beta\) est défini en termes de rapport, il est sans unité. L’unité appelée décibel (\(dB\)) est utilisée pour indiquer que ce rapport est multiplié par 10. Le niveau d’intensité sonore n’est pas le même que l’intensité sonore - il vous indique le niveau du son par rapport à une intensité de référence plutôt que l’intensité réelle.
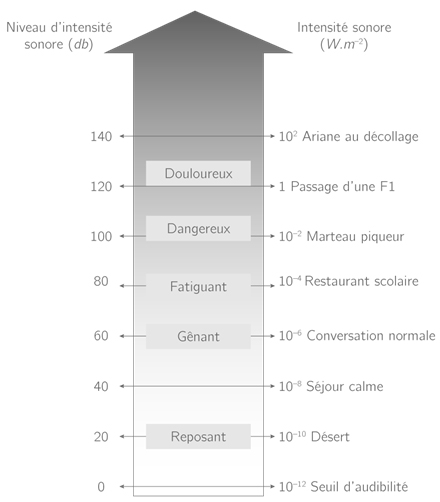
Fig. 3.10 Intensités et niveaux sonores pour l’oreille humaine#
Exemples de problèmes d’intensité des ondes sonores#
Calcul des niveaux d’intensité sonore
Calculer le niveau d’intensité sonore en décibels pour une onde sonore se déplaçant dans l’air à \(0°C\) et ayant une amplitude de pression de \(0.656\,Pa\).
stratégie
On nous donne \(\Delta p\), on peut donc calculer \(I\) à l’aide de l’équation \(I = \frac{(\Delta p)^{2}}{2\rho v_{son}}\). En utilisant \(I\), on peut calculer \(\beta\) directement à partir de sa définition dans \(\beta\,(dB) = 10{\ log}_{10}\left( \frac{I}{I_{0}} \right)\).
solution
Identifier les valeurs connues :
Le son se déplace à \(331\,m/s\) dans l’air à \(0°C\).
L’air a une densité de \(1.29\,kg/m^3\) à la pression atmosphérique et à \(0°C\).
Entrez ces valeurs et l’amplitude de pression dans \(I = \frac{(\Delta p)^{2}}{2\rho v_{son}}\) .
\[I = \frac{(\Delta p)^{2}}{2\rho v_{w}} = \frac{\left( 0.656\text{~Pa} \right)^{2}}{2\left( 1.29\text{~kg/m}^{3} \right)\left( 331\text{~m/s} \right)} = 5.04 \cdot 10^{- 4}\text{~W/m}^{2}\]Entrez la valeur de \(I\) et la valeur connue de \(I_0\) dans \(\beta\,(dB)= 10\text{~log}_{10}\left(\frac{I}{I_{0}}\right)\). Calculez pour trouver le niveau d’intensité sonore en décibels.
\[10\text{~log}_{10}\left( 5.04 \times 10^{8} \right) = 10(8.70)\text{~dB} = 87.0\text{~dB.}\]
discussion
Ce son de \(87.0\,dB\) a une intensité cinq fois supérieure à celle d’un son de \(80\,dB\). Ainsi, un facteur cinq d’intensité correspond à une différence de \(7\,dB\) dans le niveau d’intensité sonore. Cette valeur est vraie pour toutes les intensités différant d’un facteur cinq.
Changer les niveaux d’intensité d’un son : qu’arrive-t-il au niveau de décibels ?
Montrez que si un son est deux fois plus intense qu’un autre, il a un niveau sonore supérieur d’environ \(3\,dB\).
stratégie
On vous donne que le rapport de deux intensités est de 2 à 1, et on vous demande ensuite de trouver la différence de leurs niveaux sonores en décibels. Vous pouvez résoudre ce problème en utilisant les propriétés des logarithmes.
solution
Identifier les valeurs connues :
Le rapport des deux intensités est de 2 à 1, soit :
\[\frac{I_{2}}{I_{1}} = 2.00\]Nous voulons montrer que la différence de niveau sonore est d’environ 3 dB. C’est-à-dire que nous voulons montrer
\[\beta_{2} - \beta_{1} = 3\text{~dB}\]À noter que
\[\text{log}_{10}b - \text{log}_{10}a = \text{log}_{10}\left(\frac{b}{a}\right)\]
Utilisez la définition de \(\beta\) pour obtenir :
\[\beta_{2} - \beta_{1} = 10\text{~log}_{10}\left( \frac{I_{2}}{I_{1}} \right) = 10\text{~log}_{10}2.00 = 10(0.301)\text{~dB}\]Donc
\[\beta_{2} - \beta_{1} = 3.01\text{~dB}\]
discussion
Cela signifie que les deux niveaux d’intensité sonore diffèrent de \(3.01\,dB\), soit environ \(3\,dB\), comme annoncé. Notez que comme seul le rapport \(I_{2}/I_{1}\) est donné (et non les intensités réelles), ce résultat est vrai pour toutes les intensités qui diffèrent d’un facteur deux. Par exemple, un son de \(56.0\,dB\) est deux fois plus intense qu’un son de \(53.0\,dB\), un son de \(97.0\,dB\) est deux fois moins intense qu’un son de \(100\,dB\), et ainsi de suite.
Exemples pratiques#
Exemple A
Calculez l’intensité d’une onde si la puissance transférée est de \(10\,W\) et que la zone à travers laquelle l’onde est transférée est de \(5\) mètres carrés.
\(200\,W / m^2\)
\(50\,W / m^2\)
\(0.5\,W / m^2\)
\(2\,W / m^2\)
solution
Solution
Exemple B
Calculez l’intensité sonore d’une onde sonore se déplaçant dans l’air à \(0°C\) et ayant une amplitude de pression de \(0.90\,Pa\).
\(1.8\cdot 10^{-3}\,W/m^{2}\)
\(4.2\cdot 10^{-3}\,W/m^{2}\)
\(1.1\cdot 10^{3}\,W/m^{2}\)
\(9.5 \cdot 10^{-4}\,W/m^{2}\)
solution
Solution
L’ouïe et la voix#
Les gens créent des sons en poussant l’air vers le haut à travers leurs poumons et à travers des plis élastiques dans la gorge appelés cordes vocales. Ces plis s’ouvrent et se ferment rythmiquement, créant une accumulation de pression. Lorsque l’air monte et dépasse les cordes vocales, il les fait vibrer. Cette vibration s’échappe de la bouche avec des bouffées d’air sous forme de son. Une voix change de hauteur lorsque les muscles du larynx se détendent ou se resserrent, ce qui modifie la tension sur les cordes vocales. Une voix devient plus forte lorsque le flux d’air des poumons augmente, ce qui augmente l’amplitude de l’onde de pression acoustique.
L’ouïe est la perception du son. Il peut nous donner beaucoup d’informations - telles que la hauteur, le volume et la direction. Les humains peuvent normalement entendre des fréquences allant d’environ \(20\) à \(20'000\,Hz\). D’autres animaux ont des amplitudes auditives différentes de celles des humains. Les chiens peuvent entendre des sons allant jusqu’à \(45'000\,Hz\), tandis que les chauves-souris et les dauphins peuvent entendre des sons allant jusqu’à \(110'000\,Hz\). Vous avez peut-être remarqué que les chiens réagissent au son d’un sifflet pour chien qui produit un son hors de portée de l’ouïe humaine.
Les sons inférieurs à \(20\,Hz\) sont appelés infrasons, tandis que ceux supérieurs à \(20'000\,Hz\) sont des ultrasons.
La façon dont nous entendons implique une physique intéressante. L’onde sonore qui frappe notre oreille est une onde de pression. L’oreille convertit les ondes sonores en impulsions nerveuses électriques, comme un microphone.
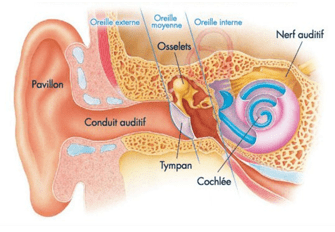
Fig. 3.11 Anatomie de l’oreille avec sa division en trois parties : l’oreille externe ou conduit auditif ; l’oreille moyenne, qui va du tympan à la cochlée ; et l’oreille interne, qui est la cochlée elle-même. La partie du corps normalement appelée oreille est techniquement appelée le pavillon.#
L’oreille externe, ou conduit auditif, transporte le son vers le tympan protégé à l’intérieur de l’oreille. L’oreille moyenne convertit le son en vibrations mécaniques et applique ces vibrations à la cochlée. Le système de levier de l’oreille moyenne prend la force exercée sur le tympan par les variations de pression acoustique, l’amplifie et la transmet à l’oreille interne via la fenêtre ovale. Deux muscles de l’oreille moyenne protègent l’oreille interne des sons très intenses. Ils réagissent à un son intense en quelques millisecondes et réduisent la force transmise à la cochlée. Cette réaction de protection peut également être déclenchée par votre propre voix, de sorte que le bourdonnement lors d’un feu d’artifice, par exemple, peut réduire les dommages causés par le bruit.
[Figure 14.12] montre l’oreille moyenne et l’oreille interne plus en détail. Lorsque les os de l’oreille moyenne vibrent, ils font vibrer la cochlée, qui contient du liquide. Cela crée des ondes de pression dans le fluide qui font vibrer la membrane tectoriale. Le mouvement de la membrane tectoriale stimule de minuscules cils sur des cellules spécialisées appelées cellules ciliées. Ces cellules ciliées, et leurs neurones attachés, transforment le mouvement de la membrane tectoriale en signaux électriques qui sont envoyés au cerveau.
La membrane tectoriale vibre à différentes positions en fonction de la fréquence du son entrant. Cela nous permet de détecter la hauteur du son. Un traitement supplémentaire dans le cerveau nous permet également de déterminer la direction d’où vient le son (en comparant le temps d’arrivée et l’intensité du son entre nos deux oreilles).
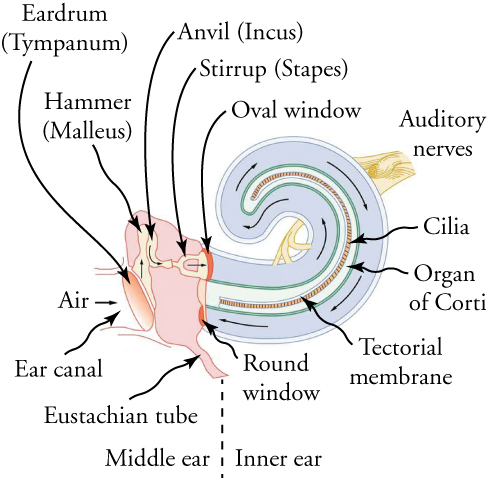
Fig. 3.12 L’oreille interne, ou cochlée, est un tube enroulé d’environ 3 mm de diamètre et de 3 cm de longueur lorsqu’il est déroulé. Lorsque l’étrier vibre contre la fenêtre ovale, il crée des ondes de pression qui traversent le liquide de la cochlée. Ces ondes font vibrer la membrane tectoriale, qui plie les cils et stimule les nerfs de l’organe de Corti. Ces nerfs envoient ensuite des informations sur le son au cerveau.#
Vérifiez votre compréhension#
Questions 1
Qu’est-ce que l’intensité sonore ?
L’intensité est l’énergie par unité de surface transportée par une onde.
L’intensité est l’énergie par unité de volume transportée par une onde.
L’intensité est la puissance par unité de surface transportée par une onde.
L’intensité est la puissance par unité de volume transportée par une onde.
réponse
Réponse 3.
Questions 2
Comment la puissance est-elle définie par rapport à une onde sonore ?
La puissance est la vitesse à laquelle l’énergie est transférée par une onde sonore.
La puissance est la vitesse à laquelle la masse est transférée par une onde sonore.
La puissance est la vitesse à laquelle l’amplitude d’une onde sonore change.
La puissance est la vitesse à laquelle la longueur d’onde d’une onde sonore change.
réponse
Réponse 1.
Questions 3
Quel mot ou expression est utilisé pour décrire l’intensité du son ?
Fréquence ou oscillation
Niveau d’intensité ou décibel
Timbre
Pas
réponse
Réponse 2.
Questions 4
Quelle est l’expression mathématique du niveau d’intensité sonore \(\beta\) ?
\(\beta\,(dB) = 10{\ log}_{10}\left( \frac{I_{0}}{I} \right)\)
\(\beta\,(dB) = 20{\ log}_{10}\left( \frac{I}{I_{0}} \right)\)
\(\beta\,(dB) = 20{\ log}_{10}\left( \frac{I_{0}}{I} \right)\)
\(\beta\,(dB) = 10{\ log}_{10}\left( \frac{I}{I_{0}} \right)\)
réponse
Réponse 4.
Questions 5
Quelle est la gamme de fréquences que les humains sont capables d’entendre ?
\(20\,Hz\) à \(200'000\,Hz\)
\(2\,Hz\) à \(50'000\,Hz\)
\(2\,Hz\) à \(2'000\,Hz\)
\(20\,Hz\) à \(20'000\,Hz\)
réponse
Réponse 4.
Questions 6
Comment les humains changent-ils la hauteur de leur voix ?
Détendre ou resserrer la glotte
Détendre ou resserrer leur luette
Détendre ou resserrer la langue
Détendre ou resserrer le larynx
réponse
Réponse 4.
