2.4. Ondes stationnaires

Parfois, les vagues ne semblent pas bouger et elles semblent simplement rester en place, vibrer. De telles ondes sont appelées ondes stationnaires et sont formées par la superposition de deux ou plusieurs ondes se déplaçant dans des directions opposées. Les vagues se déplacent les unes à travers les autres avec leurs perturbations qui s’ajoutent au fur et à mesure qu’elles passent. Si les deux ondes ont la même amplitude et la même longueur d’onde, elles alternent entre interférences constructives et destructrices. Les ondes stationnaires créées par la superposition de deux ondes identiques se déplaçant dans des directions opposées sont illustrées dans les Fig. 2.21 et Fig. 2.22.

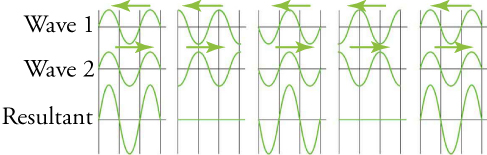
Fig. 2.21 Une onde stationnaire est créée par la superposition de deux ondes identiques se déplaçant dans des directions opposées. Les oscillations se produisent à des endroits fixes dans l’espace et résultent d’une alternance d’interférences constructives et destructrices.

À titre d’exemple, on peut voir des ondes stationnaires à la surface d’un verre de lait dans un réfrigérateur. Les vibrations du moteur du réfrigérateur créent des ondes sur le lait qui oscillent de haut en bas mais ne semblent pas se déplacer sur la surface. Les deux ondes qui produisent des ondes stationnaires peuvent être dues aux réflexions sur le côté du verre.

Les tremblements de terre peuvent créer des ondes stationnaires et provoquer des interférences constructives et destructrices. Lorsque les ondes sismiques se propagent le long de la surface de la Terre et se réfléchissent sur des roches plus denses, des interférences constructives se produisent en certains points. Par conséquent, les zones les plus proches de l’épicentre ne sont pas endommagées, tandis que les zones plus éloignées de l’épicentre sont endommagées.

Les ondes stationnaires se trouvent également sur les cordes des instruments de musique et sont dues aux réflexions des ondes des extrémités de la corde Fig. 2.22.

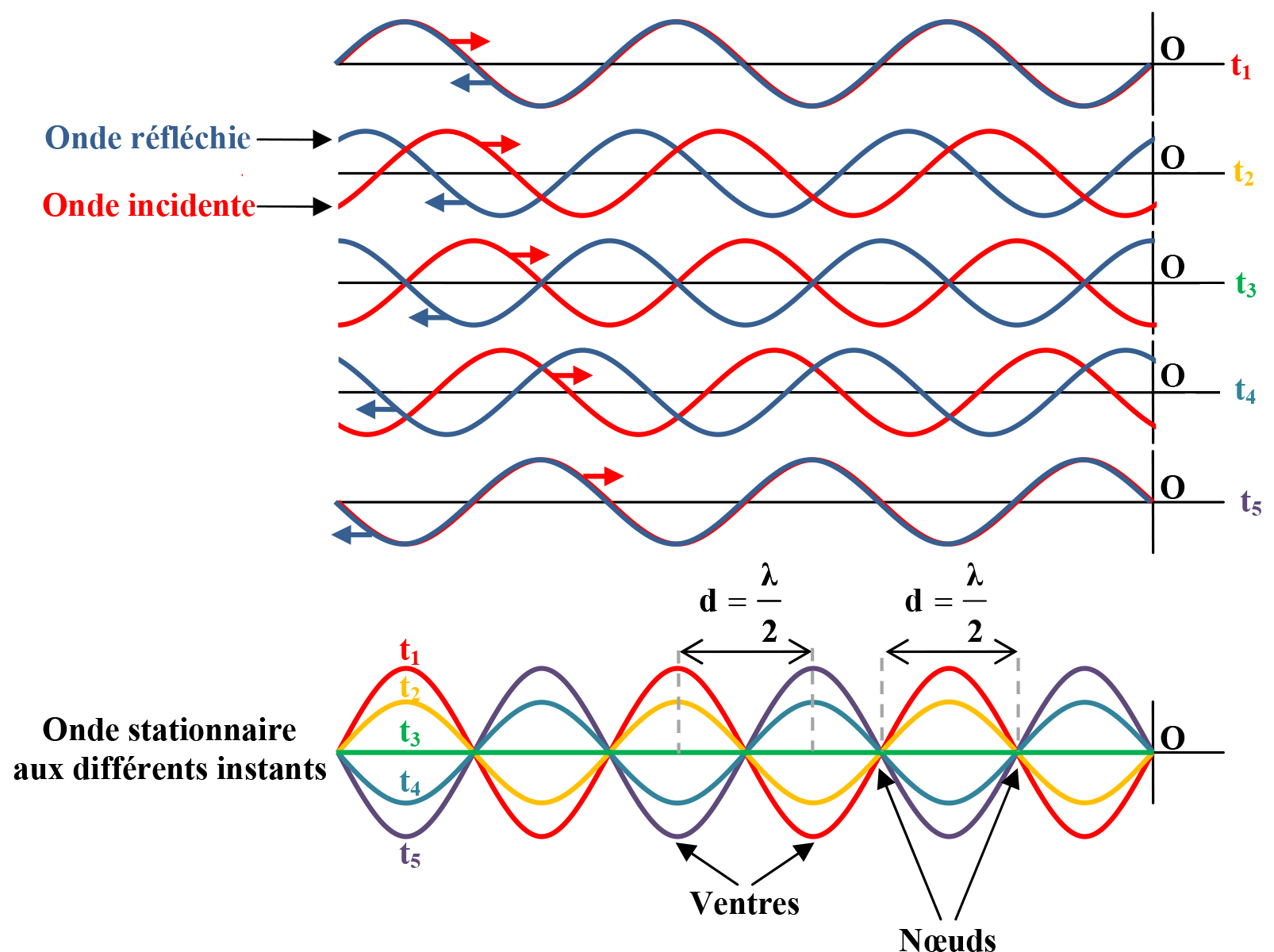
Fig. 2.22 Création d’une onde stationnaire dans une corde.

La Fig. 2.23 et la Fig. 2.24 montrent trois ondes stationnaires qui peuvent être créées sur une corde fixée aux deux extrémités. Lorsque l’onde atteint l’extrémité fixe, elle n’a nulle part où aller si ce n’est de retourner d’où elle vient, provoquant la réflexion. Les nœuds sont les points où la chaîne ne se déplace pas ; Plus généralement, les noeuds sont les points où la perturbation de l’onde est nulle dans une onde stationnaire. Les extrémités fixes des chaînes doivent également être des nœuds, car la chaîne ne peut pas s’y déplacer.

Les ventres sont l’emplacement de l’amplitude maximale dans les ondes stationnaires. Les ondes stationnaires sur une corde ont une fréquence qui est liée à la vitesse de propagation \(v_{w}\) de la perturbation sur la corde. La longueur d’onde \(\lambda\) est déterminée par la distance entre les points où la chaîne est fixée en place.

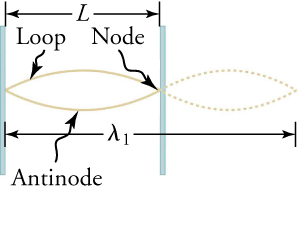
Fig. 2.23 La figure montre une corde oscillant avec sa perturbation maximale comme ventre.

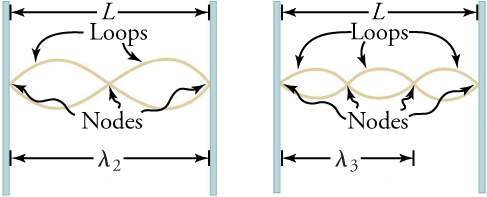
Fig. 2.24 La figure montre une chaîne oscillant avec plusieurs nœuds.

Réflexion et réfraction des ondes

Comme nous l’avons vu dans le cas des ondes stationnaires sur les cordes d’un instrument de musique, la réflexion est le changement de direction d’une onde lorsqu’elle rebondit sur une barrière, telle qu’une extrémité fixe. Lorsque l’onde atteint l’extrémité fixe, elle change de direction et retourne à sa source. Lorsqu’elle est réfléchie, l’onde subit une inversion, ce qui signifie qu’elle se retourne verticalement. Si une vague frappe l’extrémité fixe avec une crête, elle reviendra sous forme de creux, et vice versa. Reportez-vous à la Fig. 2.25.

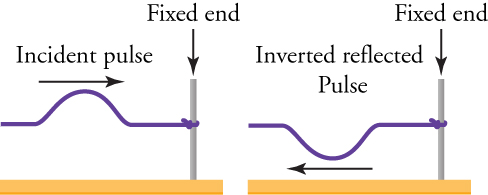
Fig. 2.25 Une onde est inversée après réflexion à partir d’une extrémité fixe.

Conseils pour réussir

Si la fin n’est pas fixe, on dit qu’il s’agit d’une fin libre, et aucune inversion ne se produit. Lorsque l’extrémité est lâchement attachée, elle se réfléchit sans inversion, et lorsque l’extrémité n’est attachée à rien, elle ne réfléchit pas du tout. Vous l’avez peut-être remarqué en modifiant les paramètres de Extrémité fixée à Extrémité libre à Pas d'extrémité dans la simulation PhET Onde sur une corde du chapitre sur la propriétés des ondes.

Plutôt que de rencontrer une extrémité fixe ou une barrière, les ondes passent parfois d’un milieu à un autre, par exemple, de l’air à l’eau. Différents types de milieux ont des propriétés différentes, telles que la densité ou la profondeur, qui affectent la façon dont une onde les traverse. À la frontière entre les milieux, les ondes subissent une réfraction—elles changent de chemin de propagation. Au fur et à mesure que l’onde se plie, elle change également de vitesse et de longueur d’onde en entrant dans le nouveau milieu. Reportez-vous à la Fig. 2.26.

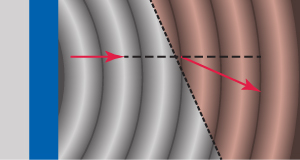
Fig. 2.26 Une onde se réfracte lorsqu’elle pénètre dans un milieu différent.

Par exemple, les vagues d’eau qui se déplacent de la partie profonde à la partie peu profonde d’une piscine subissent une réfraction. Ils se plient dans une trajectoire plus proche de la perpendiculaire à la surface de l’eau, se propagent plus lentement et diminuent en longueur d’onde à mesure qu’ils pénètrent dans des eaux moins profondes.

PhET simulation

Ondes mécaniques sur une corde

Ondes stationnaire dans une corde

Lorsqu’on fait vibrer une corde dont les deux extrémités sont fixes, on crée toute une série d’ondes qui se propagent vers les extrémités de la corde, y sont réfléchies puis interfèrent. En interférant les unes avec les autres, la plupart de ces ondes vont rapidement disparaître; seules persistent les ondes stationnaires dont les fréquences correspondent aux fréquences de résonance de la corde.

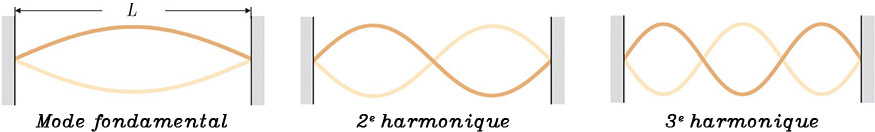
Fig. 2.27 Les trois premiers modes d’oscillation d’une corde de longueur \(L\). (crédit : Lafrance3)

Comme les deux extrémités de la corde sont fixes, elles correspondent forcement à des nœuds. En se référant à cette condition,, on peut décrire les différents modes de vibration possibles de la corde :

Mode fondamental

Le mode fondamental ou harmonique d’ordre \(n=1\) est le plus simple. Il est constitué de deux nœuds (aux extrémités) et d’un ventre. La longueur d’onde \(\lambda_{1}\) vaut le double de la longueur \(L\) de la corde :

\[\lambda_{1}=2\cdot L\]

La fréquence correspondante est donnée à partir de la vitesse de propagation (2.1) :

\[f_{1}=\dfrac{v_w}{\lambda_{1}}=\dfrac{v_w}{2\cdot L}\]

En exprimant la vitesse de propagation en fonction de la tension \(F\) et de la masse linéaire \(\mu\) de la corde (2.2), on obtient finalement :

\[f_{1}=\dfrac{1}{2\cdot L}\cdot \sqrt{\dfrac{F}{\mu}}\]

Harmonique d’ordre 2

L’harmonique d’ordre \(n=2\) (ou deuxième harmonique) contient trois nœuds et deux ventres.

La longueur d’onde \(\lambda_{2}\) est égale à la longueur \(L\) de la corde :

\[\lambda_{2}=L\]

La fréquence correspondante est donnée à partir de la vitesse de propagation :

\[f_{2}=\dfrac{v_w}{\lambda_{3}}=\dfrac{v_w}{L}\]

On obtient finalement :

\[f_{2}=\dfrac{2}{2\cdot L}\cdot \sqrt{\dfrac{F}{\mu}}\]

Harmonique d’ordre 3

L’harmonique d’ordre \(n=3\) (ou troisième harmonique) contient quatre nœuds et trois ventres.

Par une analyse similaire, on obtient la fréquence correspondante :

\[f_{3}=\dfrac{3}{2\cdot L}\cdot \sqrt{\dfrac{F}{\mu}}\]

En comparant les trois premières fréquences obtenues, on se rend compte qu’elles sont multiples de la fréquence fondamentale. On en déduit que toute la série des fréquences possibles est donnée par :

Fréquences des harmoniques d’une corde

Dans une corde, les fréquences des différentes ondes stationnaires (n^ième harmonique) sont données par :

(2.3)\[f_{n}=\dfrac{n}{2\cdot L}\cdot v_{w}=\dfrac{n}{2\cdot L}\cdot \sqrt{\dfrac{F}{\mu}}\]

où \(n\) est un entier positif (\(n \in \mathbb{N}^{*})\).

avec :

• \(f_{n}\) la fréquence de l’harmonique d’ordre \(n\) en Hertz \([Hz]\)

• \(L\) la longueur de la corde en mètre \([m]\)

• \(v_w\) la vitesse de l’onde sur la corde tendue

• \(F\) la tension de la corde en Newton \([N]\)

• \(\mu\) la masse linéaire de la corde en kilogramme par mètre \([kg/m]\)

Ondes stationnaire dans un tuyau

Lorsqu’on souffle dans une bouteille, on perçoit un son d’autant plus aigu que la bouteille est remplie. On crée de cette façon des ondes stationnaires directement dans la colonne d’air au-dessus du liquide de la bouteille. Il se produit un phénomène analogue dans les tuyaux d’un orgue ou dans une clarinette.

Dans les instruments de musique à vent (comme un orgue), certains tuyaux sont ouverts aux deux extrémités alors que d’autres tuyaux ont une extrémité ouverte et une extrémité fermée. Dans tous les cas, l’extrémité fermée correspond à un nœud de vibration et l’extrémité ouverte correspond à un ventre de vibration.

Tuyau ouvert/ouvert

Pour un tuyau de longueur \(L\) ouvert aux deux extrémités (Fig. 2.28) :

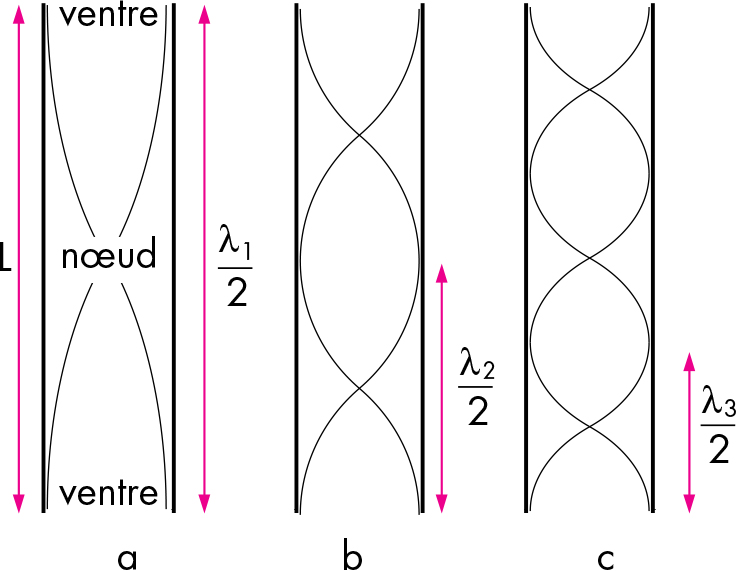
Fig. 2.28 Représentation schématique des ondes stationnaires de déplacement de l’air dans un tuyau ouvert aux deux extrémités. (a) Fondamentale. (b) Deuxième harmonique. (c) Troisième harmonique. (crédit : AKPP)

Mode fondamental

Le mode fondamental ou harmonique d’ordre \(n=1\) est le plus simple. Il est constitué d’un ventre à chaque extrémité et d’un nœud.

La longueur d’onde de la fondamentale vaut le double de \(L\) :

\[\lambda_{1}=2\cdot L\]

et sa fréquence donnée par :

\[f_{1}=\dfrac{v_{son}}{\lambda_{1}}=\dfrac{v_{son}}{2\cdot L}\]

où \(v_{son}\) représente la vitesse de propagation du son dans l’air; aux conditions normales, \(v_{son}=343\,[m/s]\).

Harmonique d’ordre 2

L’harmonique d’ordre \(n=2\) (ou deuxième harmonique) est constituée de trois ventres et deux nœuds.

La longueur d’onde correspondante est égale à la longueur \(L\) du tuyau :

\[\lambda_{1}=L\]

et sa fréquence vaut :

\[f_{2}=\dfrac{v_{son}}{\lambda_{2}}=\dfrac{v_{son}}{L}=\dfrac{2\cdot v_{son}}{2\cdot L}\]

Harmonique d’ordre 3

L’harmonique d’ordre \(n=3\) (ou troisième harmonique) est constituée de quatre ventres et trois nœuds.

La longueur d’onde correspondante est égale aux deux tiers de la longueur \(L\) du tuyau (\(\lambda_{3}=\frac{2}{3}L\)) et sa fréquence vaut :

\[f_{3}=\dfrac{v_{son}}{\lambda_{3}}=\dfrac{3\cdot v_{son}}{2\cdot L}\]

Ces fréquences sont multiples de la fondamentale; la série de toutes les fréquences possibles est donnée par :

Fréquences des harmoniques d’un tuyau ouvert/ouvert

Dans un tuyau ouvert aux deux extrémités, les fréquences des différentes ondes stationnaires (n^ième harmonique) sont données par :

(2.4)\[f_{n}=\dfrac{v_{son}}{\lambda_{n}}=\dfrac{n\cdot v_{son}}{2\cdot L}\]

où \(n\) est un entier positif (\(n \in \mathbb{N}^{*}\)).

avec :

• \(f_{n}\) la fréquence de l’harmonique d’ordre \(n\) en \([Hz]\)

• \(L\) la longueur du tuyau en \([m]\)

• \(v_{son}\) la vitesse du son dans le milieu en \([m/s]\) (dans l’air, \(v_{son}=343\,m/s\))

Tuyau ouvert/fermé

Pour un tuyau de longueur \(L\) ouvert à une extrémité et fermé à l’autre (Fig. 2.29) :

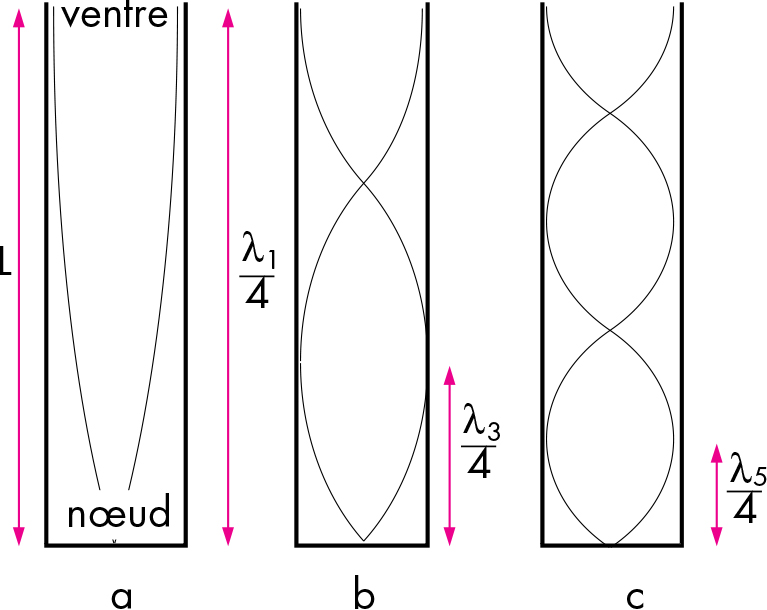
Fig. 2.29 Représentation schématique des ondes stationnaires dans un tuyau ouvert à une extrémité et fermé à l’autre. (a) Fondamentale. (b) Deuxième harmonique. (c) Troisième harmonique. (crédit : AKPP)

Mode fondamental

Le mode fondamental ou harmonique d’ordre \(n=1\) est constitué d’un ventre à une extrémité et d’un nœud à l’autre.

La longueur d’onde de la fondamentale vaut le quadruple de \(L\) (\(\lambda_{1}=4L\)) et sa fréquence est donnée par :

\[f_{1}=\dfrac{v_{son}}{\lambda_{1}}=\dfrac{v_{son}}{4\cdot L}\]

Harmonique d’ordre 2

L’harmonique d’ordre \(n=2\) (ou deuxième harmonique) est constituée de deux ventres et deux nœuds.

La longueur d’onde correspondante est égale aux quatre tiers de la longueur \(L\) du tuyau (\(\lambda_{2}=\frac{4}{3}L\)) et sa fréquence vaut :

\[f_{2}=\dfrac{v_{son}}{\lambda_{2}}=\dfrac{3\cdot v_{son}}{4\cdot L}\]

Harmonique d’ordre 3

L’harmonique d’ordre \(n=3\) (ou troisième harmonique) est constituée de trois ventres et trois nœuds.

La longueur d’onde correspondante est égale aux quatre cinquièmes de la longueur \(L\) du tuyau (\(\lambda_{3}=\frac{4}{5}L\)) et sa fréquence vaut :

\[f_{3}=\dfrac{v_{son}}{\lambda_{3}}=\dfrac{5\cdot v_{son}}{4\cdot L}\]

Ces fréquences sont des multiples impairs de la fondamentale ; la série de toutes les fréquences possibles est donnée par :

Fréquences des harmoniques d’un tuyau ouvert/fermé

Dans un tuyau ouvert à une extrémité et fermé à l’autre, les fréquences des différentes ondes stationnaires (n^ième harmonique) sont données par :

\[f_{n}=\dfrac{v_{son}}{\lambda_{n}}=\dfrac{(2n-1)\cdot v_{son}}{4\cdot L}\]

où \(n\) est un entier positif (\(n \in \mathbb{N}^{*}\)).

avec :

• \(f_{n}\) la fréquence de l’harmonique d’ordre \(n\) en \([Hz]\)

• \(L\) la longueur du tuyau en \([m]\)

• \(v_{son}\) la vitesse du son dans le milieu en \([m/s]\) (dans l’air, \(v_{son}=343\,m/s\))

Vérifiez votre compréhension

Questions 1

Qu’est-ce qu’une onde stationnaire ?

1. Des vagues qui semblent rester au même endroit et ne semblent pas bouger

2. Des vagues qui semblent se déplacer le long d’une trajectoire

réponse

Réponse 1.

Des vagues qui semblent rester au même endroit et ne semblent pas bouger.

Questions 2

Comment se forment les ondes stationnaires ?

1. Les ondes stationnaires sont formées par la superposition de deux ou plusieurs ondes se déplaçant dans des directions opposées.

2. Les ondes stationnaires sont formées par la superposition de deux ou plusieurs ondes se déplaçant dans la même direction.

3. Les ondes stationnaires sont formées par la superposition de deux ou plusieurs ondes se déplaçant dans des directions perpendiculaires.

4. Les ondes stationnaires sont formées par la superposition de deux ou plusieurs ondes se déplaçant dans des directions arbitraires.

réponse

Réponse 1.

Les ondes stationnaires sont formées par la superposition de deux ou plusieurs ondes se déplaçant dans des directions opposées.

Questions 3

Qu’est-ce que le reflet d’une onde ?

1. La réflexion d’une onde est le changement d’amplitude d’une onde lorsqu’elle rebondit sur une barrière.

2. La réflexion d’une onde est le changement de fréquence d’une onde lorsqu’elle rebondit sur une barrière.

3. La réflexion d’une onde est le changement de vitesse d’une onde lorsqu’elle rebondit sur une barrière.

4. La réflexion d’une vague est le changement de direction d’une vague lorsqu’elle rebondit sur une barrière.

réponse

Réponse 4.

La réflexion d’une vague est le changement de direction d’une vague lorsqu’elle rebondit sur une barrière.

On peut éventuellement accepter la réponse 3. puisque, en changeant de direction, la direction, et uniquement la direction de la vitesse de l’onde change

Questions 4

Qu’est-ce que l’inversion d’une onde ?

1. L’inversion se produit lorsqu’une onde se réfléchit sur une extrémité fixe et que l’amplitude de l’onde change de signe.

2. L’inversion se produit lorsqu’une onde se réfléchit sur une extrémité libre et que l’amplitude de l’onde change de signe.

3. L’inversion se produit lorsqu’une onde se réfléchit sur une extrémité fixe sans que le signe de changement d’amplitude de l’onde.

4. L’inversion se produit lorsqu’une onde se réfléchit sur une extrémité libre sans que le signe de changement d’amplitude de l’onde.

réponse

Réponse 1.

L’inversion se produit lorsqu’une onde se réfléchit sur une extrémité fixe et que l’amplitude de l’onde change de signe.