3.3. Effet Doppler et bangs soniques

L’effet Doppler des ondes sonores

L’effet Doppler est un changement dans la hauteur observée d’un son, dû à un mouvement relatif entre la source et l’observateur. Un exemple de l’effet Doppler dû au mouvement d’une source se produit lorsque vous êtes immobile, et le son d’une sirène provenant d’une ambulance passe d’un ton aigu à un ton grave au fur et à mesure qu’il passe. Plus l’ambulance est proche de vous, plus le changement est soudain. Plus l’ambulance se déplace rapidement, plus le décalage est important. Nous entendons également ce changement de fréquence pour les voitures de course, les avions et les trains qui passent.

Qu’est-ce qui cause l’effet Doppler ? Comparons trois scénarios différents : les ondes sonores émises par une source stationnaire (Fig. 3.13), les ondes sonores émises par une source en mouvement (Fig. 3.14) et les ondes sonores émises par une source stationnaire mais entendues par des observateurs en mouvement (Fig. 3.15). Dans chaque cas, le son se propage à partir du point où il a été émis.

Si la source et les observateurs sont stationnaires, les observateurs de chaque côté voient la même longueur d’onde et la même fréquence que celles émises par la source. Mais si la source se déplace et continue d’émettre du son lorsqu’elle se déplace, les compressions d’air (crêtes) se rapprochent dans la direction dans laquelle elle se déplace et s’éloignent dans la direction dont elle s’éloigne. Par conséquent, la longueur d’onde est plus courte dans la direction dans laquelle la source se déplace (à droite dans Fig. 3.14), et plus longue dans la direction opposée (à gauche dans Fig. 3.14).

Enfin, si les observateurs se déplacent, comme dans Fig. 3.15, la fréquence à laquelle ils reçoivent les compressions change. L’observateur qui se déplace vers la source les reçoit à une fréquence plus élevée (et donc à une longueur d’onde plus courte), et la personne qui s’éloigne de la source les reçoit à une fréquence plus basse (et donc à une longueur d’onde plus longue).

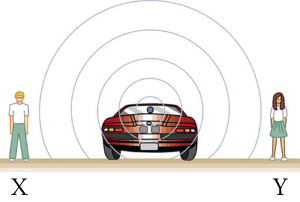
Fig. 3.13 Sons émis par une source répartis en ondes sphériques. Parce que la source, les observateurs et l’air sont stationnaires, la longueur d’onde et la fréquence sont les mêmes dans toutes les directions et pour tous les observateurs.

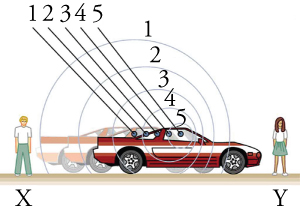
Fig. 3.14 Les sons émis par une source se déplaçant vers la droite se propagent à partir des points où ils ont été émis. La longueur d’onde est réduite et, par conséquent, la fréquence est augmentée dans le sens du mouvement, de sorte que l’observateur de droite entend un son plus aigu. L’inverse est vrai pour l’observateur de gauche, où la longueur d’onde est augmentée et la fréquence est réduite.

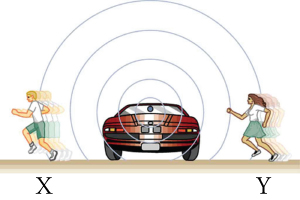
Fig. 3.15 Le même effet se produit lorsque les observateurs se déplacent par rapport à la source. Le mouvement vers la source augmente la fréquence à mesure que l’observateur de droite passe par plus de crêtes d’onde qu’il ne le ferait s’il était immobile. Le mouvement s’éloignant de la source diminue la fréquence lorsque l’observateur de gauche passe par moins de crêtes d’onde qu’il ne le ferait s’il était stationnaire.

Alerte aux idées fausses

L’effet Doppler n’est ressenti qu’en raison du mouvement relatif entre la source et l’observateur et ne dépend pas de la vitesse réelle de l’un ou l’autre.

On pourrait penser que l’effet Doppler ne se produit qu’avec les ondes sonores. Ce n’est pas le cas. Cela peut se produire avec n’importe quel type d’ondes. En fait, nous le voyons dans les ondes lumineuses qui nous parviennent d’étoiles lointaines. Ici, l’effet est observé sous la forme d’un changement de couleur.

Nous savons que la longueur d’onde et la fréquence sont liées par \(v = f\lambda\) où \(v\) est la vitesse fixe du son. Le son se déplace dans un milieu et a la même vitesse \(v\) dans ce milieu, que la source soit en mouvement ou non. Par conséquent, \(f\) multiplié par \(\lambda\) est une constante. Parce que l’observateur à droite dans Fig. 3.14 reçoit une longueur d’onde plus courte, la fréquence qu’il perçoit doit être plus élevée. De même, l’observateur de gauche reçoit une longueur d’onde plus longue et perçoit donc une fréquence plus basse.

La même chose se produit dans Fig. 3.15. Une fréquence plus élevée est perçue par l’observateur qui se déplace vers la source, et une fréquence plus basse est perçue par un observateur qui s’éloigne de la source. En général, donc, le mouvement relatif de la source et de l’observateur l’un par rapport à l’autre augmente la fréquence perçue. Le mouvement relatif à part diminue la fréquence perçue. Plus la vitesse relative est élevée, plus l’effet est important.

YouTube

Quelques liens de vidéo utiles sur le même sujet :

1. EFFET DOPPLER ✅ Explication + Formules | Terminale spécialité

Vérification de la saisie

Si vous êtes debout sur le trottoir face à la rue et qu’une ambulance passe avec sa sirène hurlante, à quel moment la fréquence que vous observez correspondra-t-elle le plus à la fréquence réelle de la sirène ?

un. quand il vient vers vous b. quand il s’éloigne de vous c. lorsqu’il est devant vous

Pour un observateur stationnaire et une source sonore en mouvement, la fréquence (f~obs~) du son perçu par l’observateur est

\(f_{obs} = f_{s}\left( \frac{v_{w}}{v_{w} \pm v_{s}} \right)\text{,}\)

14.11

où f~s~ est la fréquence du son provenant d’une source, v~s~ est la vitesse de la source le long d’une ligne joignant la source et l’observateur, et v~w~ est la vitesse du son. Le signe moins est utilisé pour le mouvement vers l’observateur et le signe plus pour le mouvement s’éloignant de l’observateur.

Conseils pour réussir

Plutôt que de se contenter de mémoriser des règles, qu’il est facile d’oublier, il est préférable de réfléchir intuitivement aux règles d’une équation. L’utilisation d’un signe moins dans \(f_{obs} = f_{s}\left( \frac{v_{w}}{v_{w} \pm v_{s}} \right)\) diminuera le dénominateur et augmentera la fréquence observée, ce qui est cohérent avec le résultat attendu de l’effet Doppler lorsque la source se déplace vers l’observateur. L’utilisation d’un signe plus augmentera le dénominateur et diminuera la fréquence observée, conformément à ce à quoi vous vous attendriez pour la source s’éloignant de l’observateur. Il peut être plus utile de garder cela à l’esprit plutôt que de mémoriser le fait que « le signe moins est utilisé pour le mouvement vers l’observateur et le signe plus pour le mouvement loin de l’observateur ».

Notez que plus la vitesse de la source est élevée, plus l’effet Doppler est important. De même, pour une source stationnaire et un observateur en mouvement, la fréquence perçue par l’observateur f~obs~ est donnée par

\(f_{obs} = f_{s}\left( \frac{v_{w} \pm v_{obs}}{v_{w}} \right)\text{,}\)

14.12

où v~obs~ est la vitesse de l’observateur le long d’une ligne joignant la source et l’observateur. Ici, le signe plus est pour le mouvement vers la source, et le signe moins est pour le mouvement s’éloignant de la source.

Booms soniques

Qu’arrive-t-il au son produit par une source en mouvement, comme un avion à réaction, qui s’approche ou même dépasse la vitesse du son ? Supposons qu’un avion à réaction vienne presque droit sur vous, émettant un son de fréquence f~s~. Plus la vitesse de l’avion est grande, v~s~, plus le décalage Doppler est important et plus la valeur de f~obs~ est élevée. Maintenant, comme v~s~ s’approche de la vitesse du son, v~w~, f~obs~ approche de l’infini, car le dénominateur dans \(f_{obs} = f_{s}\left( \frac{v_{w}}{v_{w} - v_{s}} \right)\) s’approche de zéro.

Soutien aux enseignants

[BL][OL][AL]L’équation montre qu’un bang sonique est créé lorsque la fréquence observée s’approche de l’infini. Demandez aux élèves ce qu’il advient de l’amplitude de l’onde sonore à ce moment-là. L’effet Doppler ne modifie que la fréquence du son. Cependant, lorsque toutes les ondes se superposent les unes aux autres et que leurs crêtes correspondent, l’amplitude tend également vers l’infini. C’est ce qui augmente l’intensité de la vague, créant le boom.

Ce résultat signifie qu’à la vitesse du son, devant la source, chaque onde se superpose à la précédente car la source avance à la vitesse du son. L’observateur les reçoit tous au même instant, et donc la fréquence est théoriquement infinie. Si la source dépasse la vitesse du son, aucun son n’est reçu par l’observateur jusqu’à ce que la source soit passée, de sorte que les sons de la source lorsqu’elle s’approchait sont empilés avec ceux de celle-ci lorsqu’elle s’éloigne, créant un bang sonique. Un bang sonique est une interférence constructive du son créée par un objet se déplaçant plus vite que le son.

Un aéronef crée deux bangs soniques, l’un à partir de son nez et l’autre à partir de sa queue (voir [Figure 14.17]). Lors de la couverture télévisée des atterrissages de la navette spatiale, deux explosions distinctes pouvaient souvent être entendues. Ceux-ci étaient séparés par exactement le temps qu’il faudrait à la navette pour passer d’un point. Souvent, les observateurs au sol n’observent pas l’avion qui crée le bang sonique, car il est passé avant que l’onde de choc ne les atteigne. Si l’avion vole à proximité à basse altitude, les pressions exercées dans le bang sonique peuvent être suffisamment destructrices pour briser les vitres. Pour cette raison, les vols supersoniques sont interdits au-dessus des zones peuplées des États-Unis.

! [][4]

Figure 14.17 Deux bangs soniques, créés par le nez et la queue d’un avion, sont observés au sol après le passage de l’avion.

Résolution de problèmes à l’aide de la formule de décalage Doppler

Regarder la physique

Formule de l’effet Doppler pour la fréquence observée

Cette vidéo explique la formule de l’effet Doppler pour les cas où la source se déplace vers l’observateur.

[Cliquez pour voir le contenu]

Vérification de la saisie

Disons que vous avez une phobie rare où vous avez peur de l’effet Doppler. Si vous voyez une ambulance venir vers vous, quelle serait la meilleure stratégie pour minimiser l’effet Doppler et apaiser votre doppléraphobie ?

un. Arrêtez de bouger et restez immobile jusqu’à ce qu’il passe. b. Courez vers l’ambulance. c. Courez à côté de l’ambulance.

Regarder la physique

Formule de l’effet Doppler lorsque la source s’éloigne

Cette vidéo explique la formule de l’effet Doppler dans les cas où la source s’éloigne de l’observateur.

[Cliquez pour voir le contenu]

Regardez Physique : Formule de l’effet Doppler lorsque la source s’éloigne. Cette vidéo explique en quoi la formule de l’effet Doppler diffère lorsque la source s’éloigne.

[Cliquez pour voir le contenu] [5]

Sal utilise deux formules différentes pour l’effet Doppler : l’une pour le moment où la source se déplace vers l’observateur et l’autre pour le moment où la source s’éloigne. Cependant, dans ce manuel, nous n’utilisons qu’une seule formule. Expliquer.

un. La formule combinée qui peut être utilisée est la suivante : Utilisez (+) lorsque la source se déplace vers l’observateur et (–) lorsque la source s’éloigne de l’observateur. b. La formule combinée qui peut être utilisée est f_{obs}=f_s\left(\frac{v_w\pm v_s}{v_w}\right). Utilisez (+) lorsque la source s’éloigne du point d’observation et (–) lorsque la source se déplace vers le point d’observation. c. La formule combinée qui peut être utilisée est f_{obs}=f_s\left(\frac{v_w}{v_w\pm v_s}\right) . Utilisez (+) lorsque la source se déplace vers le point d’observation et (–) lorsque la source s’éloigne du point d’observation. d. La formule combinée qui peut être utilisée est la suivante : f_{obs} = f_s\left( \frac{v_w}{v_w \pm v_s} \right). Utilisez (+) lorsque la source s’éloigne du point d’observation et (–) lorsque la source se déplace vers le point d’observation.

Exemple de travail

Calculer décalage Doppler : un klaxon de train

Supposons qu’un train équipé d’un klaxon de 150 Hz se déplace à 35 m/s dans l’air calme un jour où la vitesse du son est de 340 m/s. Quelles sont les fréquences observées par une personne immobile sur le bord des voies à l’approche du train et après son passage ?

Stratégie

Pour trouver la fréquence observée, \(f_{obs} = f_{s}\left( \frac{v_{w}}{v_{w} \pm v_{s}} \right)\) doit être utilisé car la source est en mouvement. Le signe moins est utilisé pour le train qui approche, et le signe plus pour le train qui s’éloigne.

Solution

(1) Entrez les valeurs connues dans \(f_{obs} = f_{s}\left( \frac{v_{w}}{v_{w} - v_{s}} \right)\) pour calculer la fréquence observée par une personne à l’arrêt à l’approche du train :

\(f_{obs} = f_{s}\left( \frac{v_{w}}{v_{w} - v_{s}} \right) = \left( 150\mspace{6mu}\text{~Hz} \right)\left( \frac{340\mspace{6mu}\text{~m/s}}{340\mspace{6mu}\text{~m/s} - 35\mspace{6mu}\text{~m/s}} \right)\)

\(= 167\mspace{6mu}\text{~Hz}\approx 170\mspace{6mu}\text{Hz~(2~sig.~figs.)} \)

(2) Utilisez la même équation mais avec le signe plus pour trouver la fréquence entendue par une personne immobile lorsque le train s’éloigne.

\(f_{obs} = f_{s}\left( \frac{v_{w}}{v_{w} + v_{s}} \right) = \left( 150\mspace{6mu}\text{~Hz} \right)\left( \frac{340\mspace{6mu}\text{~m/s}}{340\mspace{6mu}\text{~m/s} + 35\mspace{6mu}\text{~m/s}} \right)\)

\(= 136\mspace{6mu}\text{~Hz} \approx \text{140~Hz~(2~sig.~figs.)} \)

Discussion

Les nombres calculés sont valides lorsque le train est suffisamment éloigné pour que le mouvement se trouve presque le long de la ligne reliant le train et l’observateur. Dans les deux cas, le changement est significatif et facilement perceptible. Notez que le décalage est d’environ 20 Hz pour le mouvement vers et d’environ 10 Hz pour le mouvement vers l’extérieur. Les décalages ne sont pas symétriques.

Problèmes de pratique

15.

Quelle est la fréquence observée lorsque la source de fréquence 3,0\,\text{kHz} se déplace vers l’observateur à une vitesse de 1,0\times 10^2\,\text{m}/\text{s} et que la vitesse du son est de 331\,\text{m/s} ?

un. 3.0\,\text{kHz} b. 3.5\,\text{kHz} c. 2.3\,\text{kHz} d. 4.3\,\text{kHz}

16.

Un train s’éloigne de vous à une vitesse de 50.0\,\text{m/s}. Si vous êtes immobile et que vous entendez le sifflet à une fréquence de 305\,\text{Hz}, quelle est la fréquence réelle du sifflet produit ? (Supposons que la vitesse du son soit de 331\,\text{m/s}.)

un. 259\,\text{Hz} b. 205\,\text{Hz} c. 405\,\text{Hz} d. 351\,\text{Hz}

Vérifiez votre compréhension

17.

Qu’est-ce que l’effet Doppler ?

un. L’effet Doppler est un changement de la vitesse observée d’un son en raison du mouvement relatif entre la source et l’observateur. b. L’effet Doppler est un changement de la fréquence observée d’un son dû au mouvement relatif entre la source et l’observateur. c. L’effet Doppler est un changement dans l’intensité observée d’un son en raison du mouvement relatif entre la source et l’observateur. d. L’effet Doppler est un changement dans le timbre observé d’un son, dû au mouvement relatif entre la source et l’observateur.

18.

Donnez un exemple de l’effet Doppler causé par le mouvement de la source.

un. Le son d’un klaxon de véhicule passe d’un ton grave à un ton aigu au fur et à mesure que nous nous rapprochons de lui. b. Le son d’un klaxon de véhicule passe d’un ton grave à un ton aigu à mesure que nous nous en éloignons. c. Le son d’un klaxon de véhicule passe d’un ton grave à un ton aigu au fur et à mesure qu’il passe. d. Le son d’un klaxon de véhicule passe d’un ton aigu à un ton grave au passage.

19.

Qu’est-ce qu’un bang sonique ?

un. Il s’agit d’une interférence sonore destructrice créée par un objet se déplaçant plus vite que le son. b. Il s’agit d’une interférence constructive du son créée par un objet se déplaçant plus vite que le son. c. Il s’agit d’une interférence destructrice du son créée par un objet se déplaçant plus lentement que le son. d. Il s’agit d’une interférence constructive du son créée par un objet se déplaçant plus lentement que le son.

20.

Quelle est la relation entre la vitesse de la source et la valeur de la fréquence observée lorsque la source se déplace vers l’observateur ?

un. Ils sont indépendants l’un de l’autre. b. Plus la vitesse est élevée, plus la valeur de la fréquence observée est élevée. c. Plus la vitesse est élevée, plus la valeur de la fréquence observée est faible. d. La vitesse du son est directement proportionnelle au carré de la fréquence observée.