3.1. Vitesse du son, fréquence et longueur d’onde

Le son, comme toutes les ondes, se déplace à une certaine vitesse et possède les propriétés de fréquence et de longueur d’onde. Vous pouvez observer des preuves directes de la vitesse du son en regardant un feu d’artifice. L’éclair d’une explosion est vu bien avant que son son soit entendu, ce qui implique à la fois que le son se déplace à une vitesse finie et qu’il est beaucoup plus lent que la lumière. Vous pouvez également percevoir directement la fréquence d’un son. La perception de la fréquence est appelée tonalité. La longueur d’onde du son n’est pas directement perçue, mais des preuves indirectes se trouvent dans la corrélation de la taille des instruments de musique avec leur tonalité. Les petits instruments, comme un piccolo, produisent généralement des sons aigus, tandis que les grands instruments, comme un tuba, produisent généralement des sons graves. Une tonalité élevée signifie une petite longueur d’onde, et la taille d’un instrument de musique est directement liée aux longueurs d’onde du son qu’il produit. Ainsi, un petit instrument crée des sons de courte longueur d’onde. Des arguments similaires soutiennent qu’un grand instrument crée des sons de longue longueur d’onde.

La relation entre la vitesse du son, sa fréquence et sa longueur d’onde est la même que pour toutes les ondes :

\[v_{son}= f\lambda\]

où \(v_{son}\) est la vitesse du son, \(f\) est sa fréquence, et \(\lambda\) est sa longueur d’onde. La longueur d’onde d’un son est la distance entre des parties identiques adjacentes d’une onde, par exemple, entre des compressions adjacentes comme illustré dans la Fig. 3.1. La fréquence de l’onde est identique à celle de la source

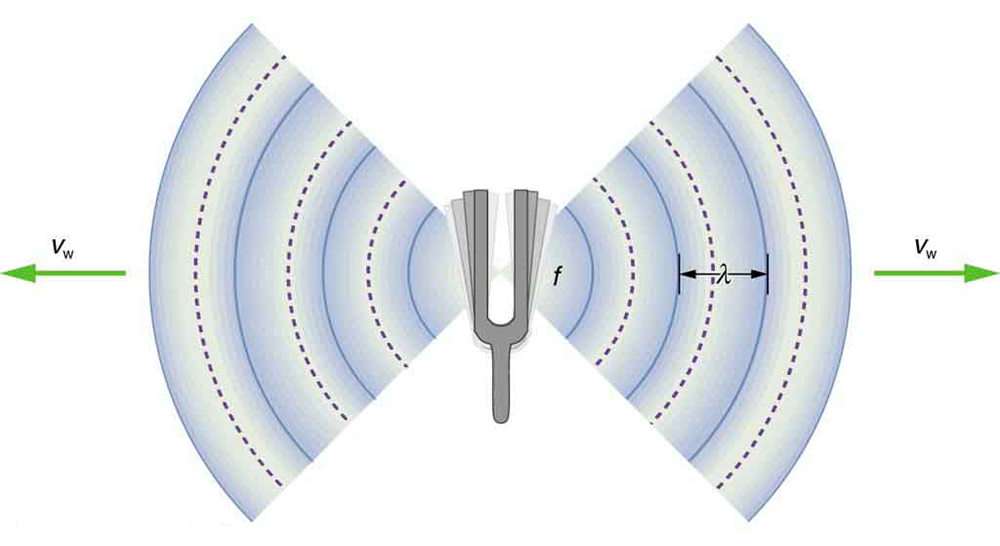
Fig. 3.1 Une onde sonore émane d’un diapason à une fréquence \(f\). Cette onde se propage à la vitesse \(v_{son}\), et a une longueur d’onde \(\lambda\).

La Table 3.1 montre clairement que la vitesse du son varie considérablement dans différents milieux. La vitesse du son dans un milieu est déterminée par une combinaison de la rigidité du milieu (ou de sa compressibilité dans les gaz) et de sa densité. Plus le milieu est rigide (ou moins compressible), plus la vitesse du son est élevée. Pour les matériaux ayant des rigidités similaires, le son se déplacera plus rapidement à travers celui ayant la densité la plus faible car l’énergie sonore est plus facilement transférée de particule à particule. La vitesse du son dans l’air est faible, car l’air est compressible. Comme les liquides et les solides sont relativement rigides et très difficiles à compresser, la vitesse du son dans de tels milieux est généralement plus élevée que dans les gaz.

Table 3.1 Vitesse du son dans différents milieux

Medium	\(\boldsymbol{v_{w}}\) (m/s)
Gaz à \(\boldsymbol{0°C}\)
Air	331
Dioxyde de carbone	259
Oxygène	316
Hélium	965
Hydrogène	1290
Gaz à \(\boldsymbol{20°C}\)
Air	343
Liquides à \(\boldsymbol{20°C}\)
Éthanol	1160
Mercure	1450
Eau douce	1440
Eau salée	1560
Tissu Humain	1540
Solides
Caoutchouc vulcanisé	54
Polyéthylène	920
Marbre	3810
Verre, Pyrex	5640
Plomb	1960
Aluminium	5120
Acier	5960
Granite	6000

La vitesse du son est affectée par la température dans un milieu donné. Pour l’air au niveau de la mer, la vitesse du son est donnée par

\[v_w = (331 m/s)\sqrt{\frac{T}{273K}}\]

où la température (notée \(T\)) est en unités de kelvin. Bien que non négligeable, cette dépendance n’est pas forte. À \(0°C\), la vitesse du son est de \(331\,m/s\), tandis qu’à \(20.0°C\), elle est de \(343\,m/s\), soit une augmentation de moins de \(4\%\).

PhET simulation

Ondes sonores

Analyse spectrale d’un son

Les sons produits par une source peuvent être de deux types :

• Le son est dit pur si l’onde sonore est une fonction sinusoïdale.

• Le son est dit complexe si l’onde sonore est périodique mais non sinusoïdale.

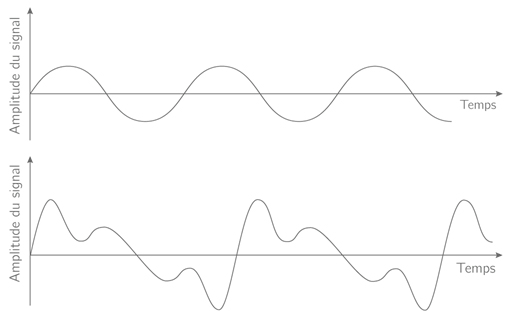
Fig. 3.2 Son pur (en haut) et son complexe (en bas).

Pour définir la composition d’un son complexe, on réalise l’analyse spectrale du son. L’analyse spectrale, aussi appelée spectre en fréquence, est la représentation graphique de l’amplitude relative d’un signal quelconque en fonction de la fréquence.

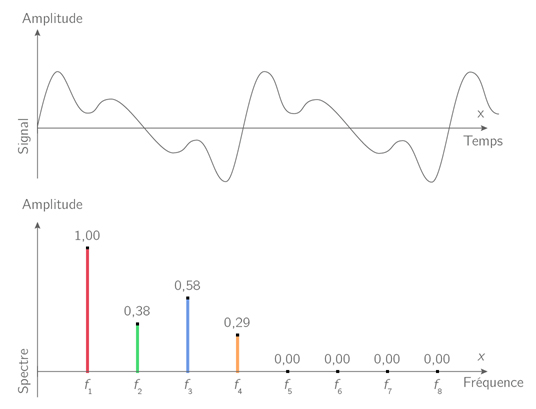
Fig. 3.3 Spectre d’un signal

Hauteur et timbre d’un son

Hauteur d’un son

La hauteur d’un son est la fréquence du signal correspondant à l’onde sonore, appelée fréquence fondamentale ou simplement fondamentale.

La Fig. 3.4 montre le signal et le spectre d’un son correspondant à la note \(La=440\,[Hz]\) émis par un diapason :

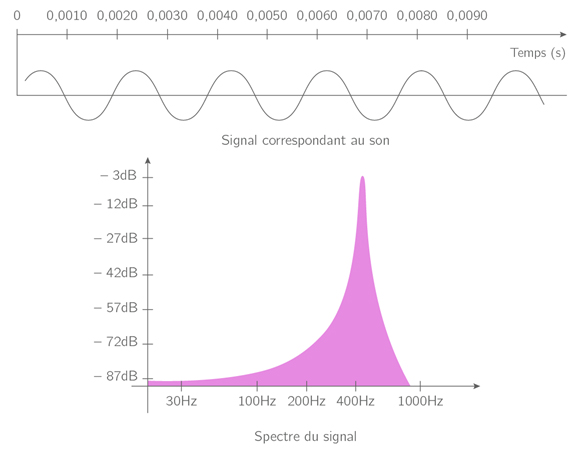
Fig. 3.4 Son pur correspondant à la note \(La\) et dont la hauteur est de \(440\,[Hz]\).

Timbre d’un son

Le timbre d’un son est défini par la présence et l’amplitude relative des différents pics du spectre en fréquence de ce son appelés harmoniques. Voici le signal et le spectre d’un son correspondant au \(La\) émis par un instrument

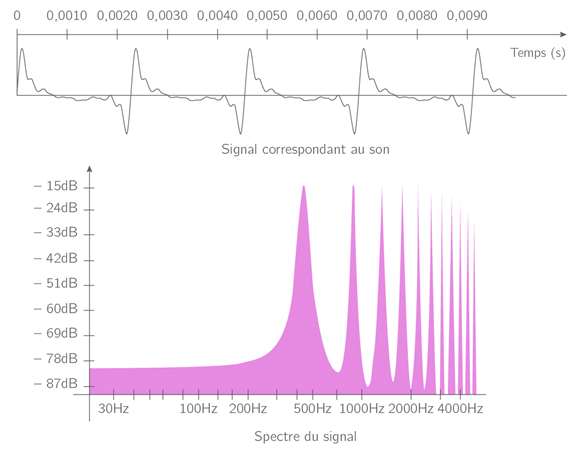
Fig. 3.5 Note \(La\) jouée par un instrument.

La hauteur de ce son est toujours de \(440\,[Hz]\) (puisque la fréquence fondamentale vaut \(440\,[Hz]\)) mais le spectre en fréquence contient de nombreuses harmoniques définissant le timbre du son complexe émis par l’instrument.

Les fréquences des harmoniques sont toutes multiples de la fréquence fondamental \(f_{1}\). Ainsi, la fréquence \(f_{n}\) d’une harmonique de rang \(n\) est: \(f_{n}=n\cdot f_{1}\)

Puisque la fréquence fondamentale d’un son correspondant à la note \(La\) est \(f_{1}=440\,[Hz]\), les fréquences de ces harmoniques sont :

• \(f_{2}=2\cdot f_{1}=2\cdot 440=880\,[Hz]\)

• \(f_{3}=3\cdot f_{1}=3\cdot 440=1320\,[Hz]\)

• \(f_{4}=4\cdot f_{1}=4\cdot 440=1760\,[Hz]\)

• etc…

C’est la différence de timbre, et donc de répartition des harmoniques, qui fait que les sons émis par deux instruments différents jouant la même note sont quand même discernables.

PhET simulation

Fourier : Faire des vagues

écholocalisation

La Fig. 3.6 montre l’utilisation de la vitesse du son par une chauve-souris pour détecter les distances. Les échos sont également utilisés dans l’imagerie médicale.

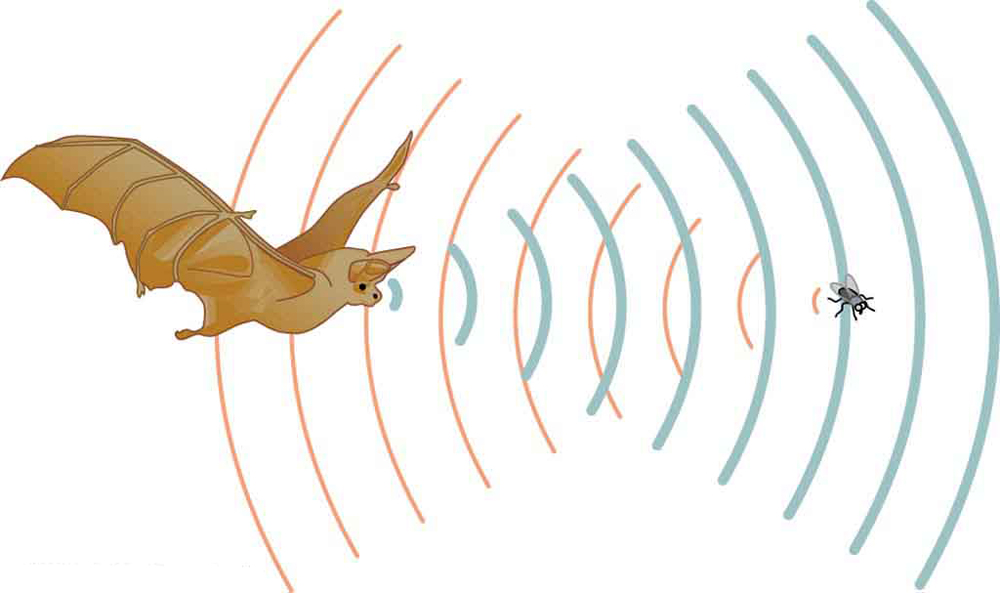
Fig. 3.6 Une chauve-souris utilise des échos sonores pour se repérer et capturer des proies. Le temps de retour de l’écho est directement proportionnel à la distance.

L’une des propriétés les plus importantes du son est que sa vitesse est presque indépendante de la fréquence. Cette indépendance est certainement vraie dans l’air libre pour les sons dans la plage audible de \(20\) à \(20'000\,Hz\). Si cette indépendance n’était pas vraie, vous le remarqueriez certainement pour la musique jouée par une fanfare dans un stade de football, par exemple. Supposons que les sons de haute fréquence se déplaçaient plus vite - alors plus vous seriez éloigné de la bande, plus le son des instruments à basse tonalité serait en retard par rapport à celui des instruments à haute tonalité. Mais la musique de tous les instruments arrive en cadence indépendamment de la distance, et donc toutes les fréquences doivent voyager à peu près à la même vitesse. Rappelez-vous que

\[v_w = f\lambda.\]

Dans un milieu donné, sous des conditions fixes, \(v_w\) est constant, de sorte qu’il existe une relation entre \(f\) et \(\lambda\) ; plus la fréquence est élevée, plus la longueur d’onde est petite.

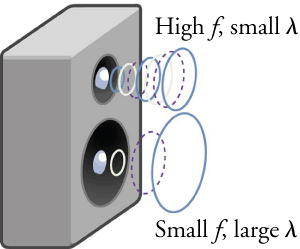
Fig. 3.7 Parce qu’elles voyagent à la même vitesse dans un milieu donné, les ondes sonores de basse fréquence doivent avoir une longueur d’onde plus grande que les ondes sonores de haute fréquence. Ici, les sons de basse fréquence sont émis par le haut-parleur large, appelé woofer, tandis que les sons de haute fréquence sont émis par le petit haut-parleur, appelé tweeter.