4.1. Qu’est-ce que l’accélération?#
Dans la conversation de tous les jours, accélérer signifie augmenter sa vitesse. L’accélérateur d’une voiture peut en effet la faire aller plus vite. Plus l’accélération est élevée, plus le changement de vitesse est important sur un temps donné. La définition formelle de l'accélération est cohérente avec ces notions, mais plus inclusive.
Accélération moyenne#
L’accélération moyenne représente la rapidité avec laquelle la vitesse change :
Accélération moyenne
Pour le mouvement à une dimension, on définit l’accélération moyenne comme étant la variation de la vitesse divisée par l’intervalle de temps correspondant :
où :
\(a\) est l’accélération moyenne
\(v_{0}\) est la vitesse initiale
\(v_{f}\) est la vitesse finale
\(\Delta t\) le temps pendant lequel la vitesse varie
L’accélération se mesure en \(\left[\dfrac{m}{s^{2}}\right]\)
Comme l’accélération est la vitesse, en \(m/s\), divisée par le temps, en \(s\), les unités SI pour l’accélération sont le \(m/s^{2}\), le mètre par seconde au carré ou mètres par seconde par seconde, ce qui signifie littéralement de combien de mètres par seconde la vitesse change chaque seconde.
Rappelez-vous que la vitesse est un vecteur - elle a à la fois une amplitude et une direction. Cela signifie qu’un changement de vitesse peut être un changement d’amplitude (ou de vitesse), mais il peut également s’agir d’un changement de direction. Par exemple, si une voiture tourne dans un virage à vitesse constante, elle accélère car sa direction change. Plus vous tournez vite, plus l’accélération est importante. Il y a donc une accélération lorsque la vitesse change soit en amplitude (augmentation ou diminution de la valeur de la vitesse), soit en direction, ou les deux.
Accélération vectorielle#
L’accélération est un vecteur dans le même sens que le changement de vitesse, \(\overrightarrow{\Delta v}\). On peut l’écrire :
Vecteur accélération
On définit le vecteur accélération \(\vec{a}\) comme étant le vecteur vitesse \(\overrightarrow{\Delta v}\) divisée par l’intervalle de temps \(t\) correspondant :
Gardez bien à l’esprit que l’accélération est toujours dans le même sens que le changement de vitesse et pas toujours dans le sens du mouvement.
Lorsqu’un objet ralentit, son accélération est opposée à la direction de son mouvement. C’est ce qu’on appelle la décélération.

Fig. 4.1 Une rame de métro à Sao Paulo, au Brésil, décélère lorsqu’elle entre dans une gare. Son accélération est dans une direction opposée à sa vitesse et à sa direction de mouvement. (crédit : Yusuke Kawasaki,Flickr)#
Alerte Idée Fausse : Accélération négative ou Décélération ?
La décélération fait toujours référence à une accélération dans la direction opposée à la direction de la vitesse. La décélération réduit toujours la vitesse. Une accélération négative, cependant, est une accélération dans la direction négative du système de coordonnées choisi. Une accélération négative peut être ou non une décélération, et une décélération peut ou non être considérée comme une accélération négative. Par exemple, considérons la Fig. 4.2.
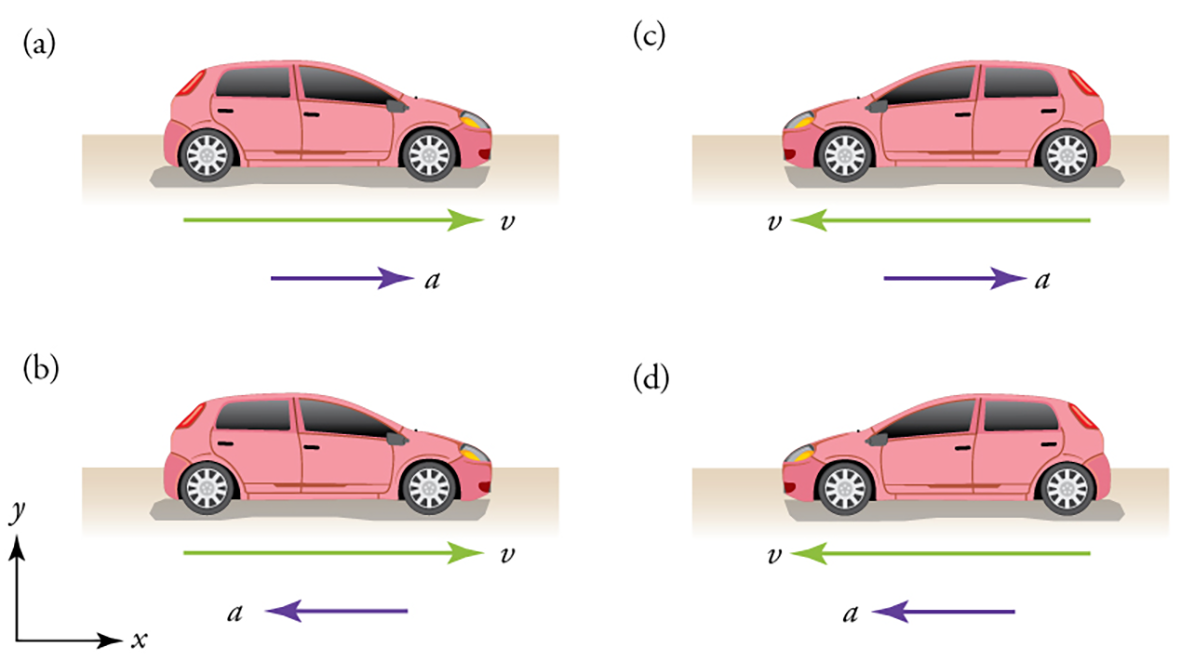
Fig. 4.2 (crédit : openstax.org).#
(a) Cette voiture accélère en se déplaçant vers la droite. Elle a donc une accélération positive dans le système de coordonnées.
(b) Cette voiture ralentit en se déplaçant vers la droite. Par conséquent, elle a une accélération négative dans le système de coordonnées, car son accélération est vers la gauche. La voiture décélère également: la direction de son accélération est opposée à sa direction de mouvement.
(c) Cette voiture se déplace vers la gauche, mais ralentit avec le temps. Par conséquent, son accélération est positive dans le système de coordonnées car elle est vers la droite. Cependant, la voiture décélère car son accélération est opposée à son mouvement.
(d) Cette voiture accélère en se déplaçant vers la gauche. Elle a une accélération négative car elle accélère vers la gauche. Cependant, comme son accélération va dans le même sens que son mouvement, elle ne décélère pas.
Exemple#
Exemple 1 - Calcul d’accélération
Un cheval de course sortant de sa porte accélère du repos à une vitesse de \(15.0\,m/s\) plein ouest en \(1.80\,s\). Quelle est son accélération moyenne?

stratégie
Nous dessinons d’abord un croquis et attribuons un système de coordonnées au problème. C’est une étape simple, mais elle aide toujours à visualiser le problème. Notez que nous attribuons l’est comme positif et l’ouest comme négatif. Ainsi, dans ce cas, nous avons une vitesse négative.
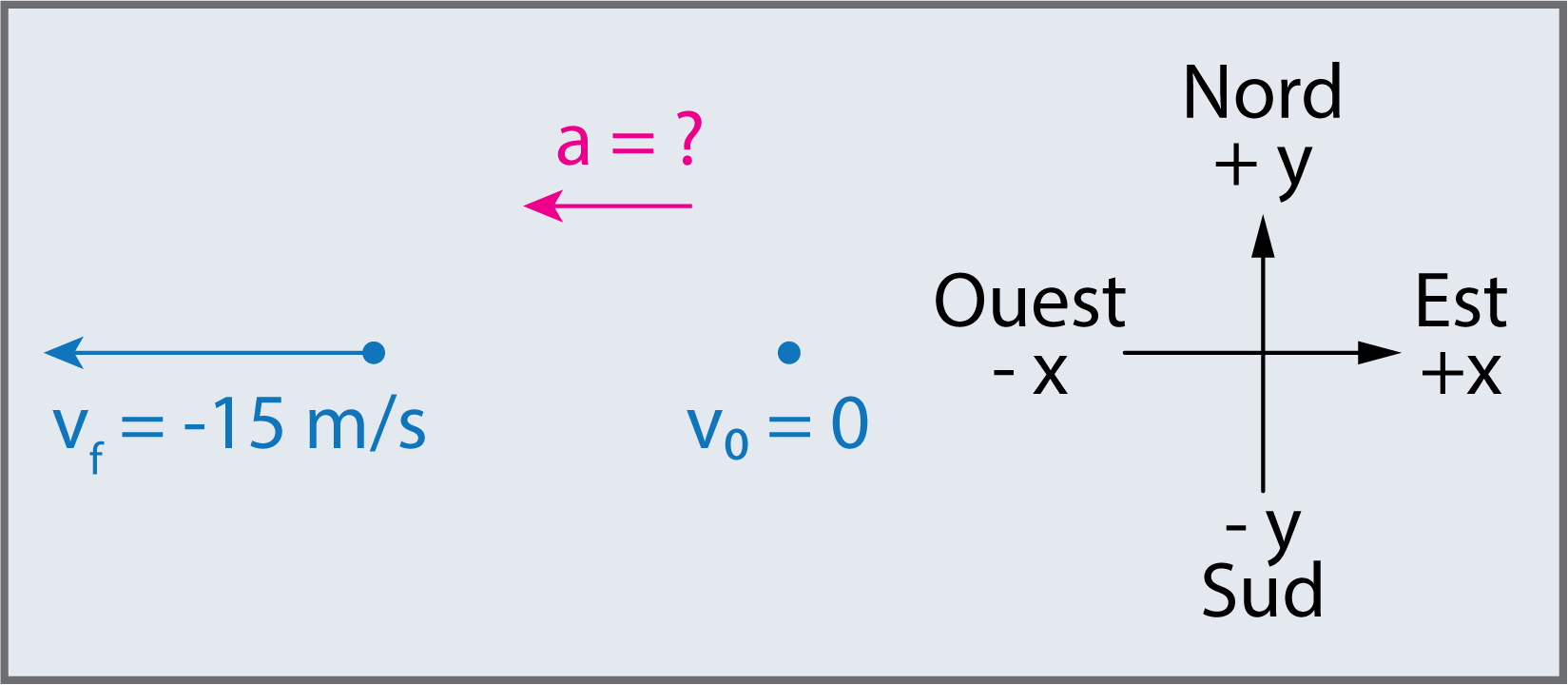
Nous pouvons résoudre ce problème en identifiant \(\Delta v\) et \(\Delta t\) à partir des informations fournies, puis calculer l’accélération moyenne directement à partir de l’équation :
solution
Identifiez les éléments connus: \(v_{0}=0\), \(v_{f}=-15.0\,m/s\) (le signe négatif indique la direction vers l’ouest), \(\Delta t=1.80\,s\)
Trouvez le changement de vitesse. Puisque le cheval passe de zéro à \(-15.0\,m/s\), son changement de vitesse est égal à sa vitesse finale: \(\Delta v=v_{f}=-15.0\,m/s\)
Appliquez les valeurs numériques connues (\(\Delta v\) et \(\Delta t\)) et résolvez l’inconnu \(a_{moy}\)
\[a_{moy}=\dfrac{\Delta v}{\Delta t}=\dfrac{-15.0\,m/s}{1.80\,s}=-8.33\,m/s^{2}\]
discussion
Le signe négatif de l’accélération indique que l’accélération est vers l’ouest. Une accélération de \(8.33\,m/s^{2}\) plein ouest signifie que le cheval augmente sa vitesse de \(8.33\,m/s\) plein ouest chaque seconde, soit \(8.33\) mètres par seconde par seconde, ce que nous écrivons comme \(8.33\,m/s^{2}\). C’est vraiment une accélération moyenne, car la conduite n’est pas douce. Nous verrons plus loin qu’une accélération de cette ampleur obligerait le cavalier à s’accrocher avec une force à peu près égale à son poids.
Accélération instantanée#
L’accélération instantanée \(a\) est obtenue par le même processus que celui décrit pour la vitesse instantanée - c’est-à-dire en considérant un intervalle de temps infiniment petit. Comment trouver une accélération instantanée en utilisant uniquement l’algèbre? La réponse est que nous choisissons une accélération moyenne qui est représentative du mouvement.
La Fig. 4.3 montre des graphiques d’accélération instantanée en fonction du temps pour deux mouvements très différents :
Dans la Fig. 4.3(a), l’accélération varie légèrement et la moyenne sur tout l’intervalle est presque la même que l’accélération instantanée à tout moment. Dans ce cas, nous devons traiter ce mouvement comme s’il avait une accélération constante égale à la moyenne (ici environ \(1.8\,m/s^{2}\)).
Dans la Fig. 4.3(b), l’accélération varie considérablement avec le temps. Dans une telle situation, il est préférable de considérer des intervalles de temps plus petits et de choisir une accélération moyenne pour chacun. Par exemple, nous pourrions considérer le mouvement sur les intervalles de temps de \(0\) à \(1.0\,s\) et de \(1.0\) à \(3.0\,s\) comme des mouvements séparés avec des accélérations de \(+3.0\,m/s^{2}\) et \(-2.0\,m/s^{2}\), respectivement.
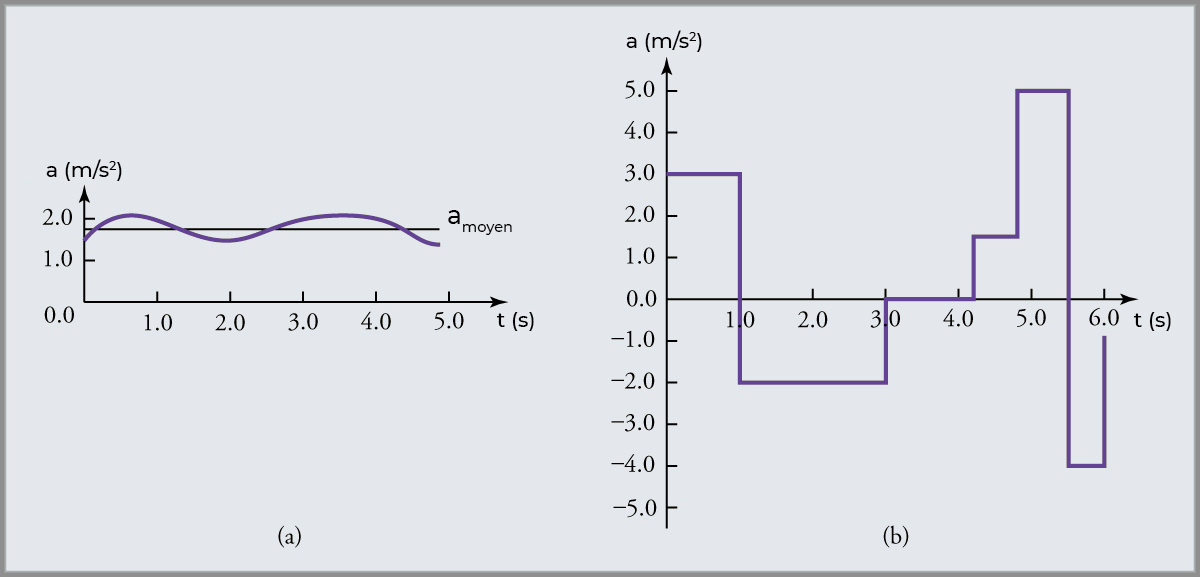
Fig. 4.3 Graphiques d’accélération instantanée en fonction du temps pour deux mouvements unidimensionnels différents. (a) Ici, l’accélération ne varie que légèrement et est toujours dans le même sens, car elle est positive. La moyenne sur l’intervalle est presque la même que l’accélération à un moment donné. (b) Ici, l’accélération varie considérablement, représentant peut-être un colis sur un tapis roulant de bureau de poste qui est accéléré vers l’avant et vers l’arrière au fur et à mesure qu’il se déplace. Il est nécessaire de considérer de petits intervalles de temps (par exemple de 0 à 1,0 s) avec une accélération constante ou presque constante. (crédit : openstax.org)#
Les quelques exemples suivants tiennent compte du mouvement de la rame de métro illustrée à la Fig. 4.4. En (a), le train se déplace vers la droite et en (b) il se déplace vers la gauche. Les exemples sont conçus pour illustrer davantage les aspects du mouvement et pour illustrer certains des raisonnements qui permettent de résoudre des problèmes.
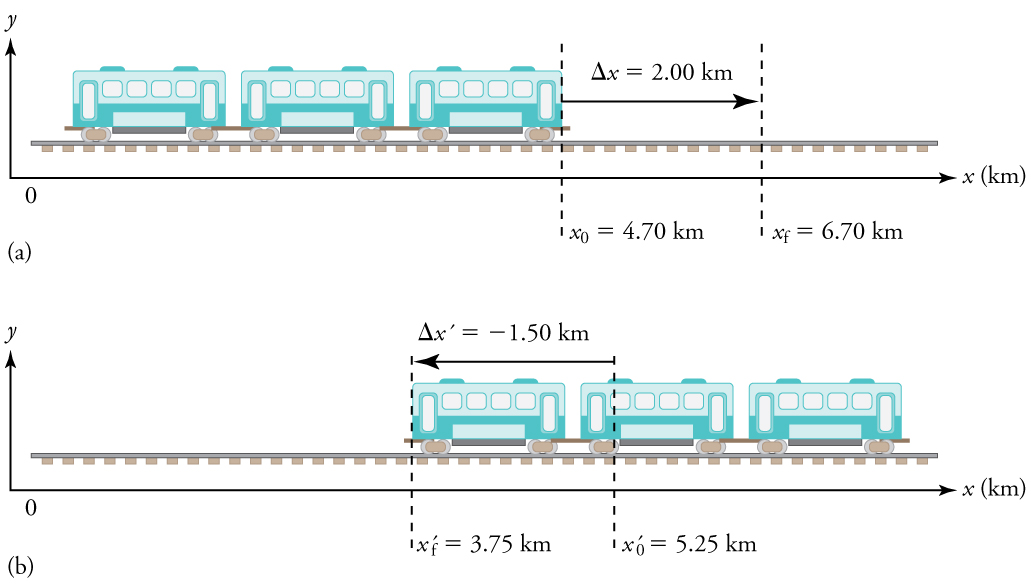
Fig. 4.4 La rame de métro - Mouvement unidimensionnel d’une rame de métro considérée dans les exemples ci-dessous. Ici, nous avons choisi l’axe \(x\) de sorte que \(+\) signifie à droite et \(-\) signifie à gauche pour les déplacements, les vitesses et les accélérations. (a) La rame de métro se déplace vers la droite de \(x_{0}\) à \(x_{f}\). Son déplacement \(\Delta x\) est de \(+2.0\,km\). (b) Le train se déplace vers la gauche de \(x'_{0}\) à \(x'_{f}\). Son déplacement \(\Delta x'\) est de \(-1.5\,km\). (Notez que le symbole prime (’) est utilisé simplement pour distinguer le déplacement dans les deux situations différentes. Les distances de déplacement et la taille des trains sont sur des échelles différentes pour tout intégrer dans le diagramme. (crédit : openstax.org)#
Exemples#
Exemple 2 - Calcul d’un déplacement
Quelle est l’amplitude et le signe (direction) des déplacements pour les mouvements de la rame de métro illustrés dans les parties (a) et (b) de la Fig. 4.4 ?
stratégie
Un dessin avec un système de coordonnées est déjà fourni, nous n’avons donc pas besoin de faire un croquis, mais nous devons l’analyser pour nous assurer de bien comprendre ce qu’il montre. Portez une attention particulière au système de coordonnées. Pour trouver le déplacement, nous utilisons l’équation \(\Delta x=x_{f}-x_{0}\). Ceci est simple puisque les positions initiale et finale sont données.
solution
Identifiez les éléments connus. Dans la figure, nous voyons que \(x_{f}=6.70\,km\) et \(x_{0}=4.70\,km\) pour la partie (a), et \(x'_{f}=3.75\,km\) et \(x'_{0}=5.25\,km\) pour la partie (b).
Résoudre le déplacement dans la partie (a).
\[\Delta x=x_{f}-x_{0}=6.70\,km-4.70\,km=+2.0\,km\]Résolvez le déplacement dans la partie (b).
\[\Delta x'=x'_{f}-x'_{0}=3.75\,km-5.25\,km=-1.50\,km\]
discussion
La direction du mouvement en (a) est à droite et donc son déplacement a un signe positif, alors que le mouvement en (b) est à gauche et a donc un signe négatif.
Exemple 3 - Comparaison de déplacement
Quelles sont les déplacements de la rame de métro pour les mouvements indiqués dans les parties (a) et (b) de la Fig. 4.4 ?
stratégie
Pour répondre à cette question, réfléchissez aux définitions de la distance et de la distance parcourue, et comment elles sont liées au déplacement. La distance entre deux positions est définie comme étant l’amplitude du déplacement, qui a été trouvée dans l’exemple 2. La distance parcourue est la longueur totale du chemin parcouru entre les deux positions.
solution
Le déplacement pour la partie (a) était de \(+2.0\,km\). Par conséquent, la distance entre les positions initiale et finale était de \(2.0\,km\) et la distance parcourue était de \(2.0\,km\).
Le déplacement de la partie (b) était \(-1.5\,km\). Par conséquent, la distance entre les positions initiale et finale était de \(1.5\,km\) et la distance parcourue était de \(1.5\,km\).
discussion
La distance est un scalaire. Elle a une amplitude mais aucun signe pour indiquer la direction.
Exemple 4 - Calcul d’une accélération
Supposons que le train de la Fig. 4.4(a) accélère du repos à \(30,0\,km/h\) dans les \(20\) premières secondes de son mouvement. Quelle est son accélération moyenne pendant cet intervalle de temps ?
stratégie
Cela vaut la peine, à ce stade, de faire un croquis simple:
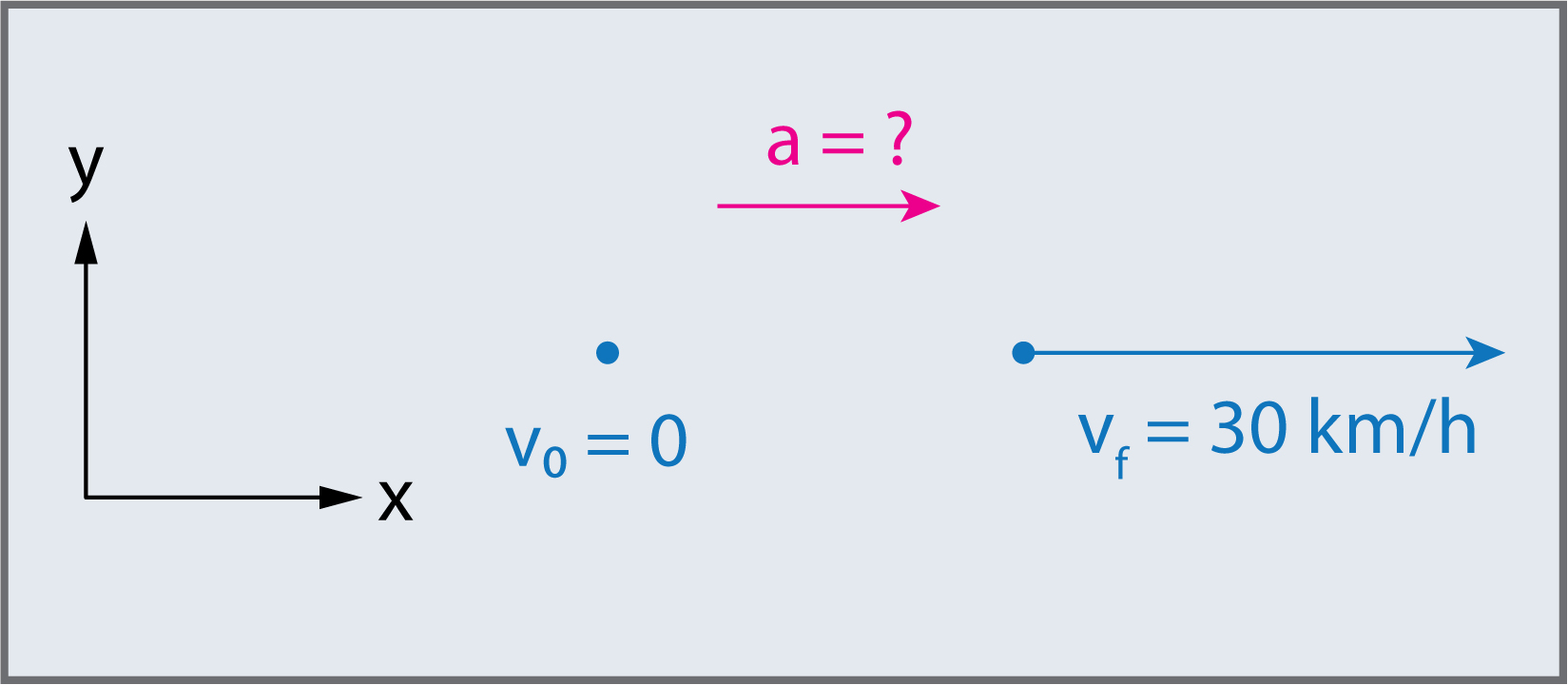
Ce problème comporte trois étapes. Nous devons d’abord déterminer le changement de vitesse, puis nous devons déterminer le changement dans le temps, et enfin nous utilisons ces valeurs pour calculer l’accélération.
solution
Identifiez les éléments connus: \(v_{0}=0\,km/h\) (le train commence au repos), \(v_{f}=30\,km/h\), et \(\Delta t=20.0\,s\).
Calculez \(\Delta v\). Puisque le train part du repos, son changement de vitesse est \(\Delta v=30,0\,km/h\), où le signe plus signifie la vitesse vers la droite.
Branchez les valeurs connues et résolvez l’inconnu, \(a_{moy}\)
\[a_{moy}=\dfrac{\Delta v}{\Delta t}=\dfrac{+30.0\,km/h}{20.0\,s}\]Puisque les unités sont mélangées (nous avons à la fois des heures et des secondes pour le temps), nous devons tout convertir en unités SI de mètres et de secondes. (Notez qu’il est souvent plus judicieux de convertir les données dans les unités SI (\(m\) et \(s\)) au début du problème.)
\[a_{moy}=\dfrac{(30.0\,km/h\,\div\,3.6)}{20.0\,s}=0.417\,m/s^{2}\]
discussion
L’accélération est positive, donc dirigée vers la droite. Ceci est raisonnable car le train part du repos et se termine avec une vitesse vers la droite (également positive). L’accélération est donc dans le même sens que le changement de vitesse, comme c’est toujours le cas.
Exemple 5 - Calcul d’une accélération
Supposons maintenant qu’à la fin de son trajet, le train de la Fig. 4.4(a) roule à une vitesse de \(30,0\,km/h\) et ralentisse pour s’arrêter en \(8.00\,s\). Quelle est son accélération moyenne jusqu’à l’arrêt ?
stratégie
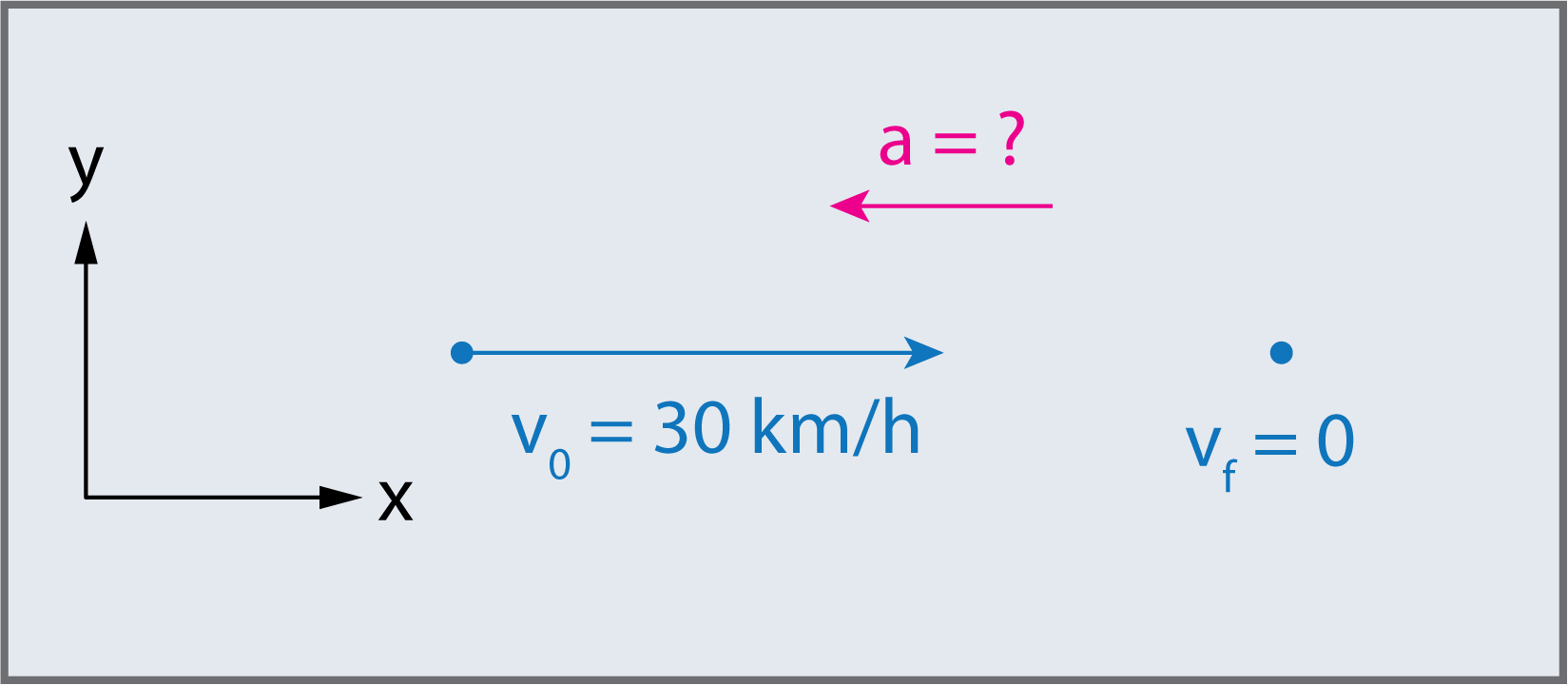
Dans ce cas, le train décélère et son accélération est négative car elle est vers la gauche. Comme dans l’exemple précédent, nous devons trouver le changement de vitesse et le changement de temps, puis calculer l’accélération.
solution
Identifiez les éléments connus: \(v_{0}=30\,km/h\), \(v_{f}=0\,km/h\) (le train est arrêté, donc sa vitesse est nulle), et \(\Delta t=8.00\,s\).
Résoudre le changement de vitesse, \(\Delta v\)
\[\Delta v=v_{f}-v_{0}=0-30\,km/h=-30\,km/h\]Branchez les éléments connus, \(\Delta v\) et \(\Delta t\) et résolvez pour \(a_{moy}\)
\[a_{moy}=\dfrac{\Delta v}{\Delta t}=\dfrac{-30.0\,km/h}{8.00\,s}\]Convertissez les unités en mètres et en secondes
\[a_{moy}=\dfrac{(-30.0\,km/h\,\div\,3 .6)}{8.00\,s}=-1.04\,m/s^{2}\]
discussion
Le signe moins indique que l’accélération est vers la gauche. Ce signe est raisonnable car le train a initialement une vitesse positive dans ce problème, et une accélération négative s’oppose au mouvement. Là encore, l’accélération va dans le même sens que le changement de vitesse, qui est ici négatif. Cette accélération peut être appelée une décélération car elle a une direction opposée à la vitesse.
Les graphiques de la position, de la vitesse et de l’accélération en fonction du temps pour les trains dans les exemples ci-dessus sont affichés dans la Fig. 4.5. (Nous avons pris la vitesse constante de \(20\,s\) à \(40\,s\), après quoi le train ralentit.)
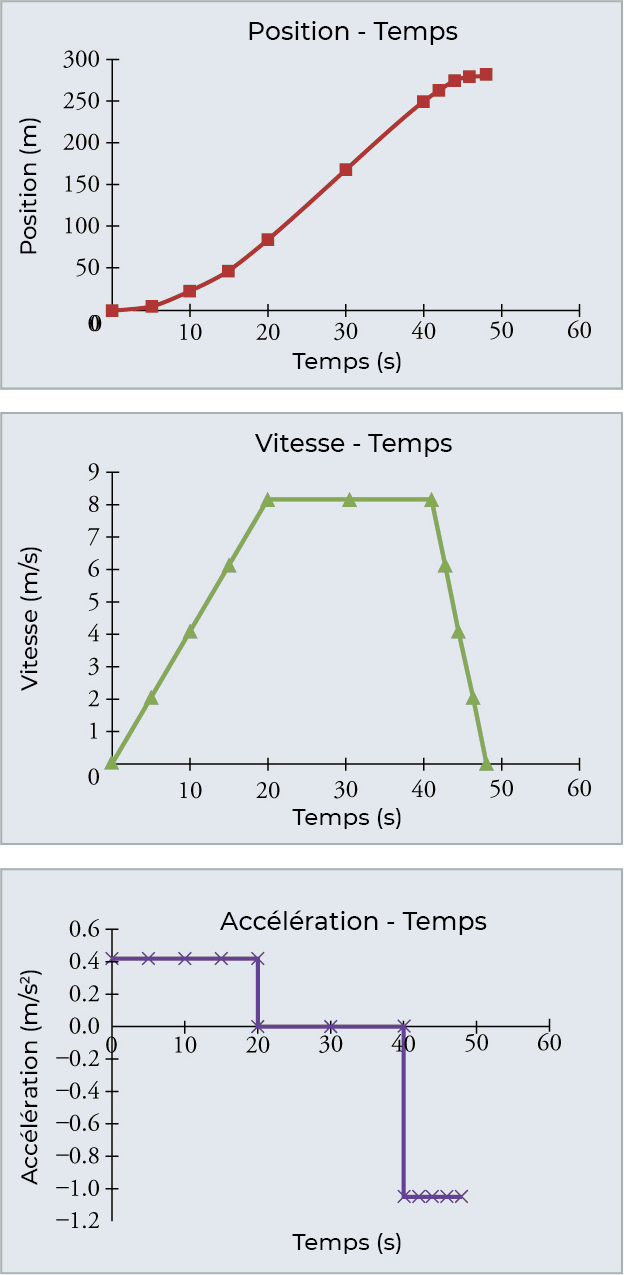
Fig. 4.5 (a) Position du train dans le temps: Remarquez que la position du train change lentement au début du voyage, puis de plus en plus rapidement à mesure qu’il prend de la vitesse. Sa position change alors plus lentement au fur et à mesure qu’il ralentit en fin de trajet. Au milieu du trajet, alors que la vitesse reste constante, la position change à une vitesse constante. (b) Vitesse du train dans le temps: La vitesse du train augmente à mesure qu’il accélère au début du voyage. Elle reste la même au milieu du trajet (là où il n’y a pas d’accélération). Elle diminue à mesure que le train décélère à la fin du voyage. (c) L’accélération du train dans le temps: Le train a une accélération positive car il accélère au début du voyage. Il n’a pas d’accélération car il se déplace à vitesse constante au milieu du voyage et a une accélération négative quand il freine à la fin. (crédit : openstax.org)#
Exemple 6 - Calcul d’une vitesse moyenne
Quelle est la vitesse moyenne du train dans la partie (b) de l’exemple 2, et illustrée à nouveau ci-dessous, s’il faut \(5.00\,min\) pour effectuer son trajet ?

stratégie
La vitesse moyenne est le déplacement divisé par le temps. Ce sera négatif ici, car le train se déplace vers la gauche et a un déplacement négatif.
solution
Identifiez les éléments connus. \(x'_{f}=3.75\,km\), \(x'_{0}=5.25\,km\), \(\Delta t=5.00\,min\).
Convertissez les unités (ici, on choisit de donner la réponse en \(km/h\)):
\[\Delta t=5.00\,min\div 60=0.0833\,h\]Déterminez le déplacement \(\Delta x'\). Nous avons trouvé \(\Delta x'=-1.50\,km\) dans l’exemple 2.
Résolvez pour la vitesse moyenne.
\[v_{moy}=\dfrac{\Delta x'}{\Delta t}=\dfrac{-1.50\,km}{0.0833\,h}=-18.0\,km/h\]
discussion
La vitesse négative indique un mouvement vers la gauche.
Exemple 7 - Calcul d’une accélération
Enfin, supposons que le train de la Fig. 4.4 ralentisse à une vitesse de \(20.0\,km/h\) pour s’arrêter en \(10.0\,s\). Quelle est son accélération moyenne?
stratégie
Encore une fois, dessinons un croquis:
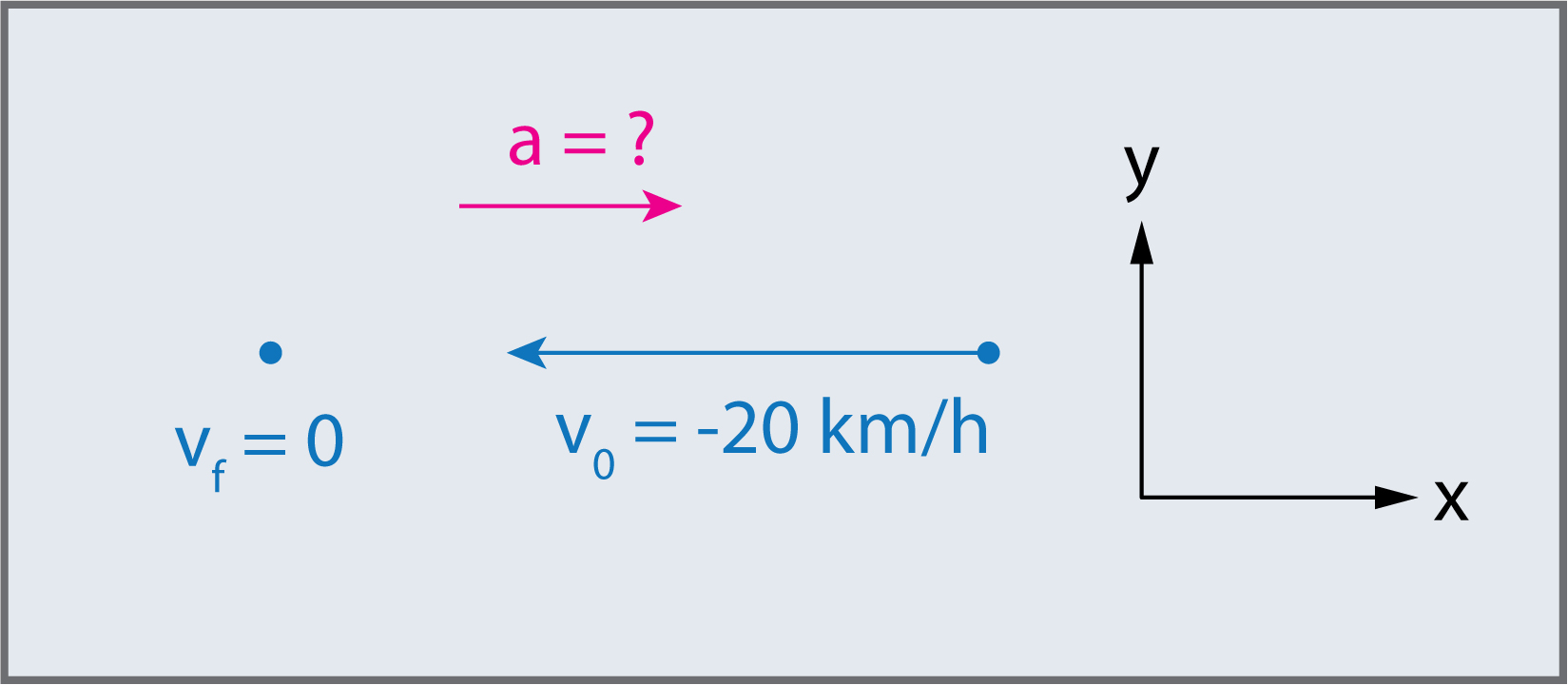
Comme précédemment, il faut trouver le changement de vitesse et le changement de temps pour calculer l’accélération moyenne.
solution
Identifiez les éléments connus: \(v_{0}=-20.0\,km/h\), \(v_{f}=0\,km/h\), \(\Delta t=10.0\,s\).
Calculez \(\Delta v\). Le changement de vitesse ici est en fait positif, car
\[\Delta v=v_{f}-v_{0}=0-(-20\,km/h)=+20\,km/h\]Convertissez les unités :
\[\Delta v=20\,km/h\,\div\,3.6=5.56\,m/s\]Résoudre pour \(a_{moy}\)
\[a_{moy}=\dfrac{\Delta v}{\Delta t}=\dfrac{5.56\,m/s}{10.0\,s}=0.556\,m/s^{2}\]
discussion
L’accélération est positive, donc dirigée vers la droite. C’est raisonnable car le train a initialement une vitesse négative (à gauche) dans ce problème et une accélération positive s’oppose au mouvement (et donc c’est à droite). Encore une fois, l’accélération va dans le même sens que le changement de vitesse, qui est positif ici. Comme dans l’exemple 5, cette accélération peut être appelée une décélération puisqu’elle est dans le sens opposé à la vitesse.
Signe et direction#
La chose la plus importante à noter à propos de ces exemples est peut-être les signes des réponses. Dans notre système de coordonnées choisi, plus (\(+\)) signifie que la quantité est à droite et moins (\(-\)) signifie qu’elle est à gauche. C’est facile à imaginer pour le déplacement et la vitesse. Mais c’est un peu moins évident pour l’accélération. La plupart des gens interprètent l’accélération négative comme le ralentissement d’un objet. Ce n’était pas le cas dans l’exemple 7, où une accélération positive ralentissait une vitesse négative. La distinction cruciale était que l’accélération était dans la direction opposée à la vitesse. En fait, une accélération négative augmentera une vitesse négative. Par exemple, le train se déplaçant vers la gauche sur la Fig. 4.4 est accéléré par une accélération vers la gauche. Dans ce cas, \(v\) et \(a\) sont négatifs. Les signes (\(+\)) et (\(-\)) donnent les directions des accélérations. Si l’accélération a le même signe que la vitesse, l’objet accélère. Si l’accélération a le signe opposé à la vitesse, l’objet ralentit.
