2.1. Vecteurs en cinématiques

2.1.1. Le vecteur déplacement

Le vecteur le plus simple est le vecteur qui représente un déplacement - le vecteur déplacement - aussi appelé changement (ou variation) de position. Lorsqu’un objet effectue un déplacement d’un point A à un point B, on dit qu’il subit un déplacement de A vers B, et on représente ce déplacement par une flèche qui pointe de A vers B. La flèche représente le vecteur de façon géométrique.

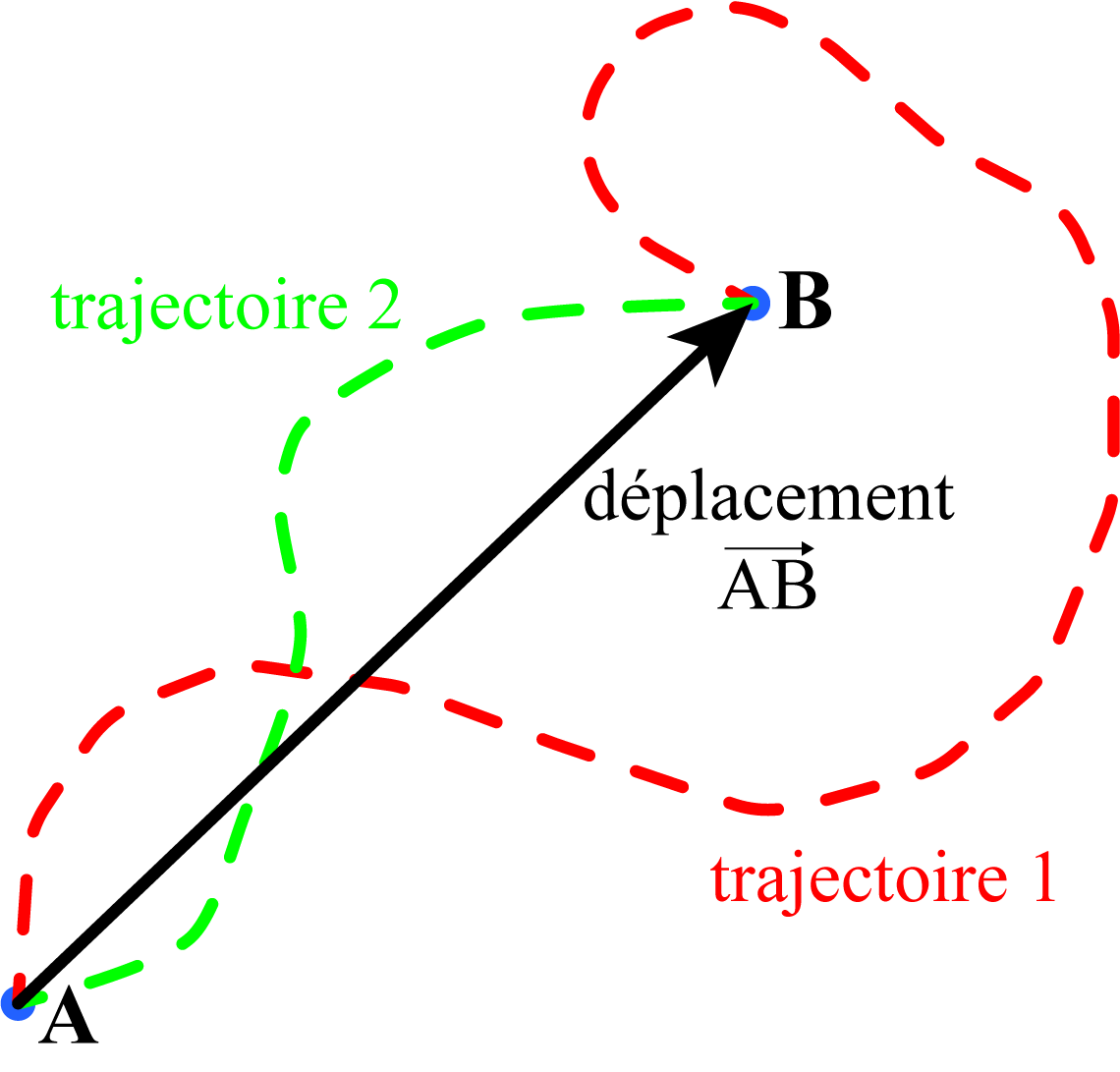
Fig. 2.1 Il existe plusieurs trajectoires possible pouvant relier A à B. Par contre le vecteur déplacement \(\overrightarrow{AB}\) est unique.

On appelle trajectoire, le parcours réel suivit par un objet. Le vecteur déplacement qui relie deux points A et B est unique, alors que ces deux points peuvent être reliés par différentes trajectoires.

Le vecteur déplacement représente seulement l’effet global du mouvement et non le mouvement lui-même.

2.1.2. Le vecteur vitesse

Le vecteur vitesse moyenne est défini de manière similaire à la vitesse moyenne scalaire :

\[\vec{v}_{moy}=\dfrac{\overrightarrow{\Delta x}}{\Delta t}\]

Géométriquement, le vecteur vitesse moyenne entre les points A et B de la trajectoire de la Fig. 2.2 est obtenu :

1. En dessinant le vecteur déplacement \(\overrightarrow{\Delta x}\) de A à B

2. En calculant l’intensité de la vitesse moyenne : \(\Vert\vec{v}_{moy}\Vert=\frac{\Vert\overrightarrow{\Delta x}\Vert}{\Delta t}\)

3. En dessinant le vecteur \(\vec{v}_{moy}\) d’origine A, de sens \(A\rightarrow B\) et de longueur \(\Vert\vec{v}_{moy}\Vert\).

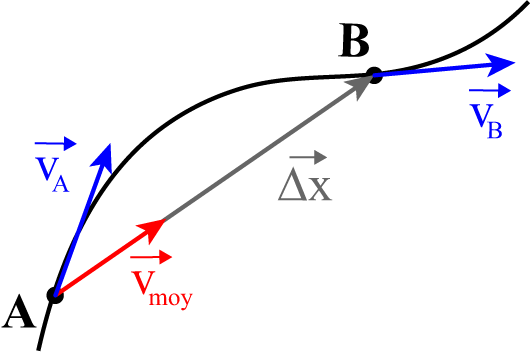
Fig. 2.2 Les vecteurs déplacement \(\vec{\Delta x}\), vitesse moyenne \(\vec{v}_{moy}\) et vitesses instantanées \(\vec{v_{A}}\) et \(\vec{v_{B}}\)

En prenant un intervalle de mesure \(\Delta t\) de plus en plus court, le point B se rapproche du point A; la vitesse instantanée est obtenue lorsque \(\Delta t\) tend vers \(0\), les points A et B sont confondus et le vecteur vitesse instantanée devient tangent à la trajectoire.

2.1.3. Le vecteur accélération

Le vecteur accélération \(\vec{a}\) exprime la variation de vitesse pendant une seconde en tenant compte du changement possible de direction du vecteur vitesse.

Pour déterminer le vecteur \(\vec{a}\), il faut d’abord construire le vecteur variation (ou différence) de vitesse \(\overrightarrow{\Delta v}=\overrightarrow{v_{2}}-\overrightarrow{v_{1}}\) en reliant l’extrémité du vecteur \(\overrightarrow{v_{1}}\) à l’extrémité du vecteur \(\overrightarrow{v_{2}}\).

Le vecteur accélération moyenne \(\vec{a}\) est le vecteur variation de vitesse \(\overrightarrow{\Delta v}\) divisé par la variation de temps \(\Delta t\) :

\[\vec{a}=\dfrac{\overrightarrow{\Delta v}}{\Delta t}\]

Pratiquement, on translatera le vecteur \(-\overrightarrow{v_{1}}\) à l’extrémité de \(\overrightarrow{v_{2}}\). \(\overrightarrow{\Delta v}\) est le vecteur qui relie l’origine de \(\overrightarrow{v_{2}}\) à l’extrémité de \(-\overrightarrow{v_{1}}\). Le vecteur \(\vec{a}\) a la même orientation que le vecteur \(\overrightarrow{\Delta v}\).

Fig. 2.3 Méthode pour tracer géométriquement le vecteur \(\vec{a}\) à partir de deux vecteurs vitesses successifs \(\vec{v}_{n}\) et \(\vec{v}_{n+1}\).

D’un point de vue vectorielle, la variation de vitesse peut prendre différents aspects :

1. La vitesse peut augmenter ou diminuer tout en gardant la même direction. C’est le cas d’une voiture qui accélère (ou qui freine) sur une route rectiligne.

2. La vitesse peut changer de direction tout en gardant la même intensité. C’est le cas d’une voiture qui effectue un virage à vitesse constante. La vitesse indiquée par le compteur ne change pas, mais il y a une accélération dirigée vers l’intérieur du virage.

3. La vitesse peut changer en direction et en intensité (une voiture qui accélère dans un virage par exemple).

Lorsqu’un objet suit une trajectoire circulaire ou en arc de cercle à vitesse (scalaire) constante, le vecteur accélération instantanée est toujours perpendiculaire au vecteur vitesse et toujours dirigé vers le centre du cercle, on parle d’accélération centripète.