5.2. Graphique de la vitesse v(t)#
A quoi sert la courbe \(v(t)\) ?#
Dans un graphique de la vitesse en fonction du temps, l’axe vertical représente la vitesse de l’objet. Cela semble évident, mais il vaut mieux être prévenu: les courbes de \(v(t)\) peuvent être difficiles à interpréter. On peut facilement oublier que l’axe vertical donne la vitesse lorsqu’on est habitué à déterminer cette dernière par la pente de la courbe de \(x(t)\).
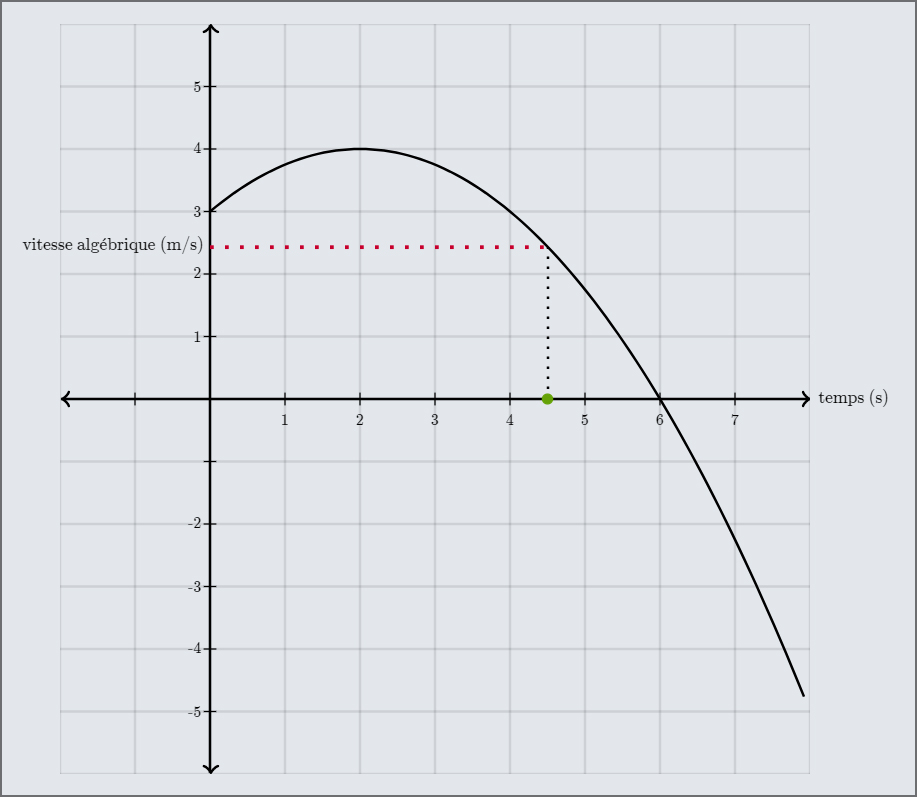
Fig. 5.5 Courbe de \(v(t)\). La vitesse de l’objet est représentée à différents instants. (crédit : khanacademy.org)#
Que représente la pente de la courbe \(v(t)\) ?#
La pente de la courbe de \(v(t)\) correspond à la variation de la vitesse. La valeur de cette pente est donc la valeur de l’accélération instantanée de l’objet.
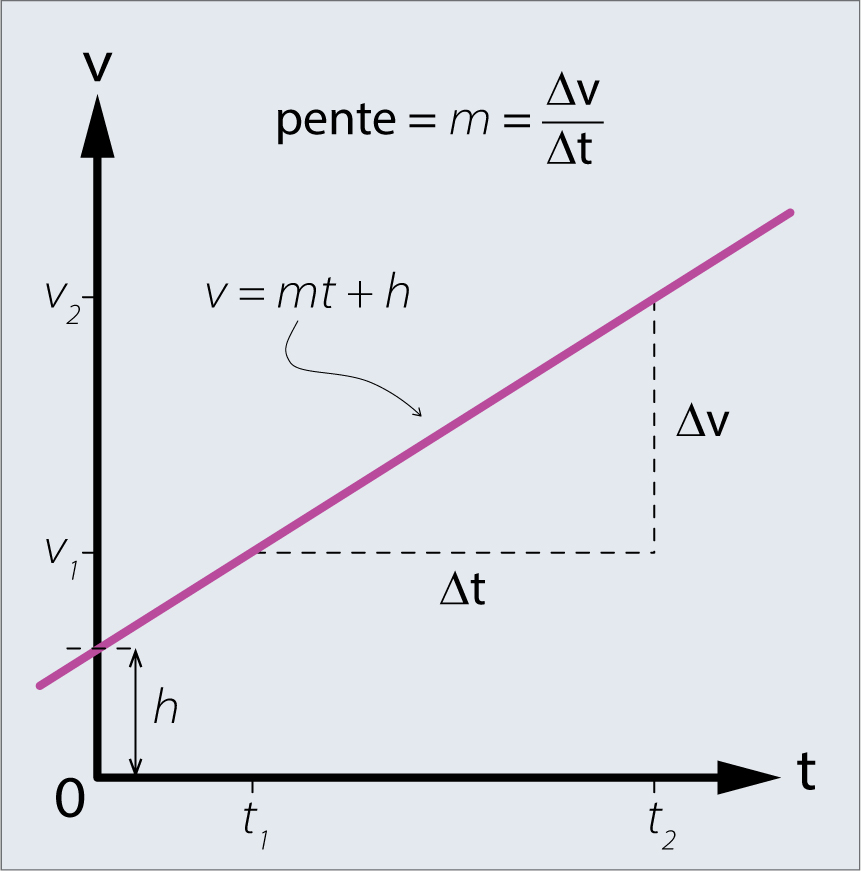
Fig. 5.6 La figure montre un graphique en ligne droite. L’équation de la ligne droite est \(v(t) = m\cdot t + h\), ou \(m\) est la pente de la droite et \(h\) sa position au temps \(t_{0}=0\).#
La pente de la courbe de \(v(t)\) est donnée par la formule suivante :
Cette expression de la pente est la même que celle de l’accélération:
Puisque, pour le mouvement à une dimension, \(\frac{\Delta v}{\Delta t}\) correspond, à l’accélération, la pente de la courbe de \(v(t)\) est égale à l’accélération de l’objet.
A retenir !
\(\boldsymbol{\rightarrow}\quad\) La pente de la courbe de \(\boldsymbol{v(t)}\) correspond à l’accélération.
Cela signifie que lorsque la pente est élevée, la vitesse de l’objet varie rapidement. A l’inverse, lorsque la pente est faible, la vitesse ne varie pas très rapidement. De plus, si la pente est négative, dirigée vers le bas, l’accélération est alors négative. A l’inverse, si la pente est positive, dirigée vers le haut, l’accélération est alors positive.
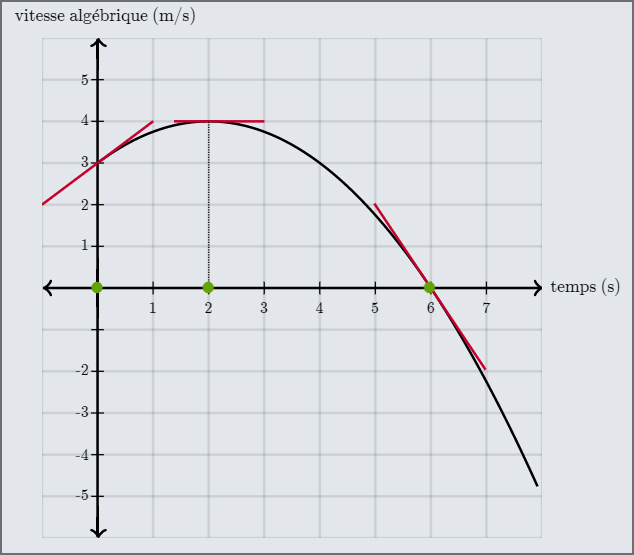
Fig. 5.7 La tangente du graphique donne la pente à un instant donné qui est égale à l’accélération de l’objet à cet instant. (crédit : khanacademy.org)#
La pente de la courbe est positive entre les instants \(t=0\,s\) et \(t=2\,s\) puisqu’elle est dirigée vers le haut. L’accélération est alors positive.
La pente de la courbe est négative entre les instants \(t=2\,s\) et \(t=8\,s\) puisqu’elle est dirigée vers le bas. L’accélération est alors négative.
A \(t=2\,s\) la pente est nulle puisque la tangente à la courbe est horizontale. L’accélération est alors nulle à cet instant.
Que représente l’aire sous la courbe \(v(t)\) ?#
L’aire sous la courbe \(v(t)\) représente le déplacement de l’objet. Pour comprendre cela, on considère ci-dessous une courbe représentant le mouvement d’un objet se déplaçant à une vitesse constante de 6 mètres par seconde pendant 5 secondes.
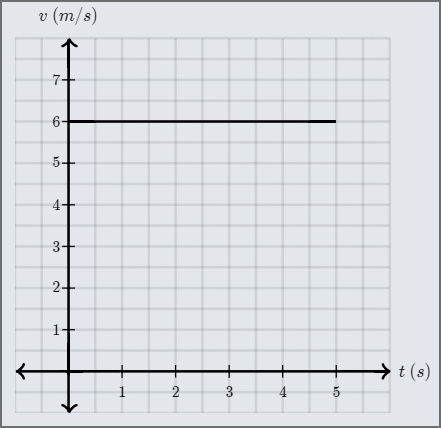
Fig. 5.8 Graphique de la vitesse d’un objet à vitesse constante. (crédit : khanacademy.org)#
Pour calculer le déplacement correspondant à cet intervalle de temps, on utilise la formule suivante:
Le déplacement est donc de \(30\,m\).
En fait, cette méthode équivaut à déterminer l’aire sous la courbe. On considère donc la surface rectangulaire ci-dessous.
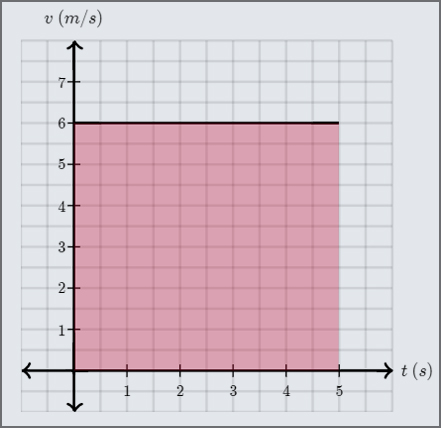
Fig. 5.9 L’aire sous la courbe correspond au déplacement. (crédit : khanacademy.org)#
L’aire de ce rectangle peut se calculer en multipliant la hauteur, \(6\,m/s\), par la largeur, \(5\,s\), ce qui donne:
On obtient donc la même chose que précédemment pour le calcul du déplacement. Pour le mouvement à une dimension, l’aire sous la courbe de \(v(t)\) est égale au déplacement durant cet intervalle de temps, peu importe la forme de la courbe
A retenir !
\(\boldsymbol{\rightarrow}\quad\) L’aire sous la courbe de \(\boldsymbol{v(t)}\) correspond au déplacement.
Graphique \(v(t)\)
Le graphique \(v(t)\) est donc très utile, puisqu’il fournit à la fois la vitesse, l’accélération et le déplacement de l’objet.
Exemple 1: Variation de vitesse en surf
Un surfeur avance en ligne droite sur une vague selon la courbe de \(v(t)\) suivante.
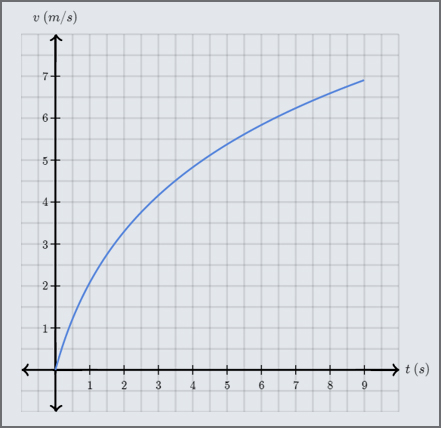
Parmi les propositions suivantes, choisir celles qui caractérisent la vitesse et l’accélération du surfeur.
Sa vitesse augmente.
Son accélération augmente.
Sa vitesse diminue.
Son accélération diminue.
solution
Seules les propositions \(1.\) et \(4.\) sont vraies.
La pente de la courbe de \(v(t)\) correspond à l’accélération. Ici, la pente diminue, cela signifie que l’accélération diminue elle aussi.
Cela pourrait sembler contre-intuitif puisqu’à en voir la courbe, la vitesse de la véliplanchiste augmente. En réalité, la valeur de cette augmentation par seconde diminue. Pour les \(4.5\) premières secondes, la vitesse est passée de \(0\,m/s\) à \(5\,m/s\), alors que pour les \(4.5\) secondes suivantes, elle est seulement passée de \(5\,m/s\) à \(7\,m/s\)
Exemple 2: Accélération en kart
La mouvement d’un kart est représenté par sa courbe \(v(t)\) ci-dessous.
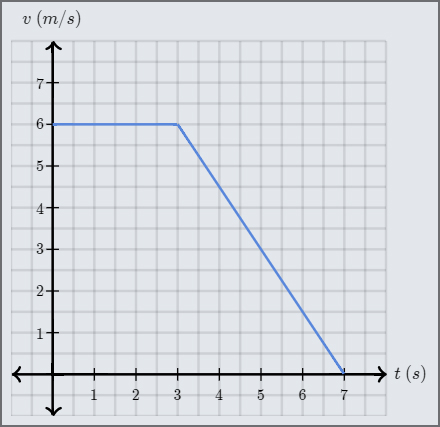
Quelle est l’accélération du kart à l’instant \(4\,s\)?
Quel est le déplacement du kart entre les instants \(0\,s\) et \(7\,s\)?
solution
- Accélération du kart à l’instant \(4\,s\) :
On détermine l’accélération à l’instant \(4\,s\) en calculant la pente de la courbe de \(v(t\)) à cet instant.
\[a=\text{pente}=\dfrac{\text{variation verticale}}{\text{variation horizontale}}\]Pour calculer la pente, on choisit, sur la partie oblique de la courbe, les deux points suivants: (\(3\,s\); \(6\,m/s\)) et (\(7\,s\); \(0\,m/s\)). On a donc:
\[a=\text{pente}=\dfrac{v_{2}-v_{1}}{t_{2}-t_{1}}=\dfrac{0\,m/s-6\,m/s}{7\,s-3\,s}=\dfrac{-6\,m/s}{4\,s}=-1.5\,m/s^{2}\]L’accélération vaut donc \(a=-1.5\,m/s^{2}\)
- Déplacement du kart entre les instants \(0\,s\) et \(7\,s\) ?
On détermine le déplacement du kart en calculant l’aire sous la courbe de \(v(t)\). Cette aire est constituée de deux parties: un rectangle, entre les instants \(0\,s\) et \(3\,s\), et un triangle, entre les instants \(3\,s\) et \(7\,s\). Une fois qu’on aura additionné les aires de ces deux formes géométriques, on aura le déplacement total.
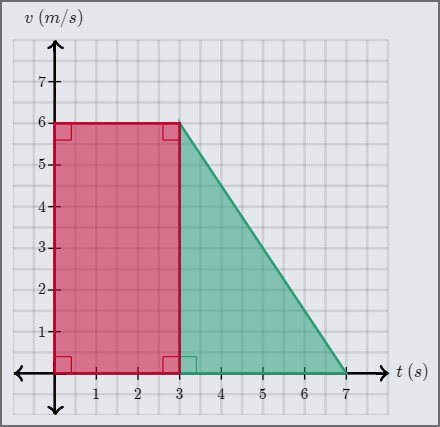
L’aire du rectangle rouge vaut \(\text{aire}_{r}=h\cdot l=6\,m/s\cdot 3\,s=18\,m\).
L’aire du triangle vert vaut \(\text{aire}_{v}=\frac{1}{2}\cdot b\cdot h=\frac{1}{2}\cdot 4\,s\cdot 6\,m/s=12\,m\).
On additionne ces deux aires \(\text{aire totale}=18\,m+12\,m=30\,m\).
Le déplacement total vaut donc \(d=30\,m\).
