3.2. Vitesse#
Vitesse moyenne#
La définition scientifique de la vitesse pour un mouvement à une dimension est similaire à la notion de vitesse dans la vie courante. On sait généralement qu’un déplacement important en un temps très court correspond à une vitesse élevée, ou encore que la vitesse s’exprime par une unité de longueur divisée par une unité de temps, comme le kilomètre par heure.
Vitesse moyenne
Pour le mouvement à une dimension, on définit la vitesse moyenne \(v_{moy}\) comme étant la variation de la position (le déplacement) divisée par l’intervalle de temps correspondant :
ou :
\(x_{0}\) est la position initiale
\(x_{f}\) est la position finale
\(t_{0}\) est le temps initial
\(t_{f}\) est le temps final
La vitesse moyenne se mesure en \(\left[\dfrac{m}{s}\right]\)
Dans cette formule, \(v_{moy}\) est la vitesse moyenne, \(\Delta x\) est la variation de la position ou encore le déplacement, et \(x_{f}\) et \(x_{0}\) sont les positions finale et initiale aux instants respectifs \(t_{f}\) et \(t_{0}\). Si l’instant initial \(t_{0}\) est égal à zéro, alors la vitesse moyenne s’écrit :
Remarque: \(t\) remplace alors \(t_{f}\).
Vecteur vitesse#
Cette définition de la vitesse est en fait la version simplifiée pour le mouvement à une dimension de la définition du vecteur vitesse. Le vecteur vitesse, défini comme le vecteur déplacement divisé par l’intervalle de temps correspondant à ce déplacement, a une direction, une norme et un sens:
Vecteur vitesse
On définit le vecteur vitesse \(\vec{v}\) comme étant le vecteur déplacement \(\overrightarrow{\Delta x}\) divisée par l’intervalle de temps \(t\) correspondant :
Dans le cadre du mouvement à une dimension, la direction est simplement celle du mouvement étudié. La norme et le sens sont les deux caractéristiques qui sont exprimées par la vitesse. Dans le Système International (SI), l’unité de la vitesse est le mètre par seconde ou \(m/s\), cependant d’autres unités comme le \(km/h\), le \(mi/h\) (noté aussi \(mph\) pour miles par heure), et le \(cm/s\) sont souvent utilisées. Si on considère, par exemple, le passager d’un avion qui a mis \(5\) secondes pour se déplacer de \(-4\) mètres, le signe moins indiquant qu’il s’est déplacé vers l’arrière de l’avion. Sa vitesse moyenne est alors :
Le signe moins indique que la vitesse moyenne est aussi orientée vers l’arrière de l’avion.
Cependant, la vitesse moyenne d’un objet ne donne pas d’information sur ce qu’il se passe entre son point de départ et son point d’arrivée. Avec la vitesse moyenne, on ne peut, par exemple, pas savoir si le passager s’est arrêté momentanément ou s’il a reculé avant de se diriger vers l’arrière de l’avion. Pour étudier cela plus en détail, il faut considérer des segments plus petits sur des intervalles de temps plus courts. Par exemple, on peut voir dans la figure ci-dessous que le déplacement total \(\Delta x_{tot}\) peut être divisé en 4 segments, \(\Delta x_{a}\), \(\Delta x_{b}\), \(\Delta x_{c}\) et \(\Delta x_{d}\).
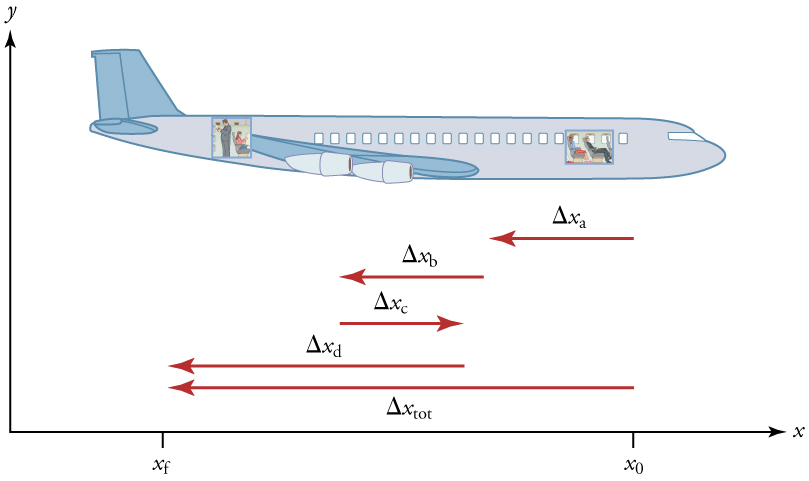
Fig. 3.5 Détail des déplacements d’un passager se dirigeant vers l’arrière de l’avion, le déplacement total étant divisé en une succession de déplacements plus petits. (crédit: openstax.org)#
Plus les intervalles de temps considérés dans le mouvement sont petits, plus la description du mouvement sera précise. En poursuivant ce raisonnement, on arrive alors à un intervalle de temps infiniment petit. Pour un tel intervalle, la vitesse moyenne devient la vitesse instantanée. Par exemple, le compteur de vitesse d’une voiture montre la valeur de la vitesse instantanée de la voiture mais pas sa direction.
C’est en se basant sur cette vitesse instantanée que la police donne des contraventions. Par contre, pour évaluer le temps qu’on mettra pour faire un trajet, il faut utiliser la vitesse moyenne. Le vecteur vitesse instantanée \(\vec{v}\) est simplement le vecteur vitesse moyenne à un instant donné, c’est à dire sur un intervalle de temps infiniment petit.
Vecteur vitesse instantanée
On définit le vecteur vitesse instantanée \(\vec{v}\) comme étant le vecteur déplacement \(\overrightarrow{\Delta x}\) divisé par intervalle de temps \(t\) qui tend vers \(0\) :
Déterminer la vitesse instantanée \(\vec{v}\) à un instant donné \(t\) nécessite de calculer une limite. C’est une opération mathématique qu’il n’est pas nécessaire de détailler au niveau de ce chapitre. En pratique, on peut souvent trouver les vitesses instantanées sans aucun calcul.
Vitesse scalaire#
Dans le langage courant, on utilise surtout la notion de vitesse scalaire, et très peu celle de vitesse. En physique, ces deux notions n’ont pas la même signification. La différence principale est que la vitesse scalaire est un scalaire (!), elle n’a pas de sens ni de direction, contrairement à la vitesse qui, elle, a un sens (sa direction étant celle du mouvement à une dimension). Tout comme on avait distingué la vitesse moyenne de la vitesse instantanée, on fait la distinction entre la vitesse scalaire moyenne et la vitesse scalaire instantanée.
La vitesse scalaire instantanée est la valeur absolue de la vitesse instantanée. Par exemple, si le passager de l’avion a une vitesse instantanée de \(-3\,m/s\) (le signe moins signifiant qu’il se dirige vers l’arrière de l’avion), sa vitesse scalaire instantanée est de \(3\,m/s\).
Autre exemple, si à un instant donné, la vitesse instantanée d’une personne en voyage est de \(40\,km/h\) vers le nord, sa vitesse scalaire instantanée est alors de \(40\,km/h\) (même valeur mais sans la direction).
La vitesse scalaire moyenne, par contre, est très différente de la vitesse moyenne. La vitesse scalaire moyenne est la distance totale parcourue divisée par le temps qui s’est écoulé. Par conséquent, bien que la vitesse scalaire instantanée et la vitesse instantanée aient la même valeur absolue, celles de la vitesse scalaire moyenne et de la vitesse moyenne peuvent être très différentes.

Fig. 3.6 Résumé des différences entre la vitesse et la vitesse scalaire.#
Puisque la distance parcourue peut être plus grande que le déplacement, la vitesse scalaire moyenne peut être plus grande que la vitesse moyenne, qui est seulement le déplacement divisé par le temps. Par exemple, si l’on fait un aller-retour de la maison jusqu’au magasin en \(30\) minutes pour une distance totale parcourue de \(6\,km\), alors la vitesse scalaire moyenne est de \(6\,km/0.5\,h=12\,km/h\). En revanche, la vitesse moyenne est nulle puisque le déplacement du trajet est nul (la position est la même au départ et à l’arrivée). La vitesse scalaire moyenne n’est donc pas simplement la valeur absolue de la vitesse moyenne.
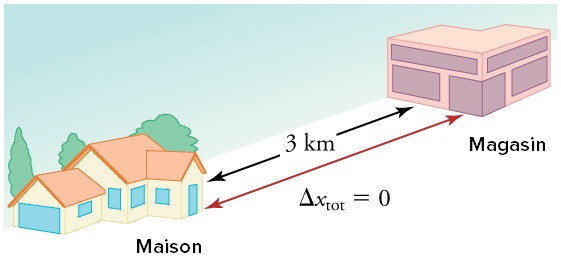
Fig. 3.7 Pour un aller-retour au magasin durant 30 minutes, la distance totale parcourue est de \(6\,km\). La vitesse scalaire moyenne est alors de \(12\,km/h\). Par contre, le déplacement lors du trajet étant nul (pas de différence entre la position initiale et la position finale), la vitesse moyenne est aussi nulle. (crédit: openstax.org)#
Un moyen très pratique de visualiser le mouvement d’un objet consiste à représenter graphiquement la position ou la vitesse de l’objet en fonction du temps. Par exemple, la Fig. 3.8 donne la position, la vitesse et la vitesse scalaire pour cet aller-retour au magasin en fonction du temps. On précise qu’on a utilisé pour cette représentation graphique une modélisation très simplifiée du mouvement: la vitesse est supposée constante, ce qui n’est pas réaliste puisqu’il y a forcément un arrêt au magasin, et le trajet entre la maison et le magasin est supposé rectiligne.
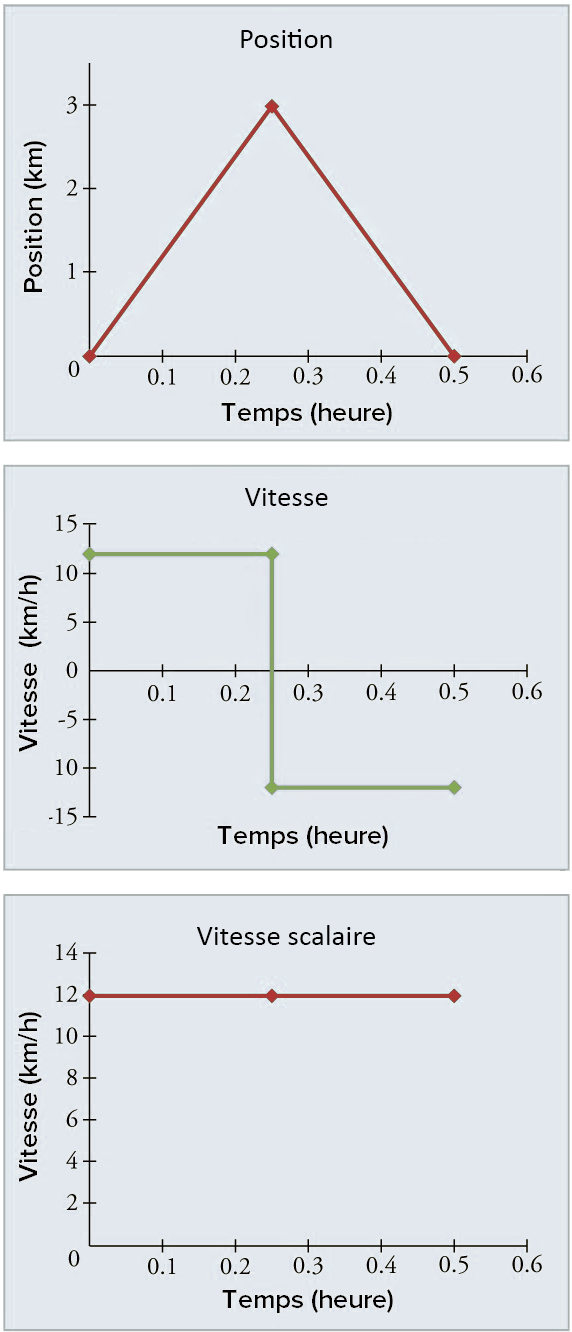
Fig. 3.8 Position en fonction du temps, vitesse en fonction du temps et vitesse scalaire en fonction du temps pour un aller-retour. On remarque que la vitesse est négative sur le retour. (crédit: openstax.org)#
Exercice résolu 1
Un iguane ayant un sens de l’orientation plus que médiocre fait des va-et-vient dans le désert. D’abord, il marche \(12\) mètres vers la droite pendant \(20\) secondes. Puis, il court \(16\) mètres vers la gauche pendant \(8\) secondes.

Quelle sont :
la vitesse scalaire moyenne et
la vitesse moyenne de l’iguane sur la totalité du trajet ?
solution
On suppose que la direction vers la droite est comptée positivement.
Pour calculer la vitesse scalaire moyenne, on considère la distance totale parcourue que l’on divise par l’intervalle de temps.
Pour calculer la vitesse moyenne, on considère le déplacement \(\Delta x\) que l’on divise par l’intervalle de temps.
L’iguane marche 12 mètres vers la droite et court 16 mètres vers la gauche. Il finit donc 4 mètres à gauche de son point de départ. Le déplacement pour tout ce trajet est de 4 mètres vers la gauche, donc \(-4\,m\).
Exercice résolu 2
Un dauphin nage horizontalement et fait des va-et-vient cherchant de la nourriture. Son mouvement est décrit ci-dessous par la représentation graphique de sa position en fonction du temps.
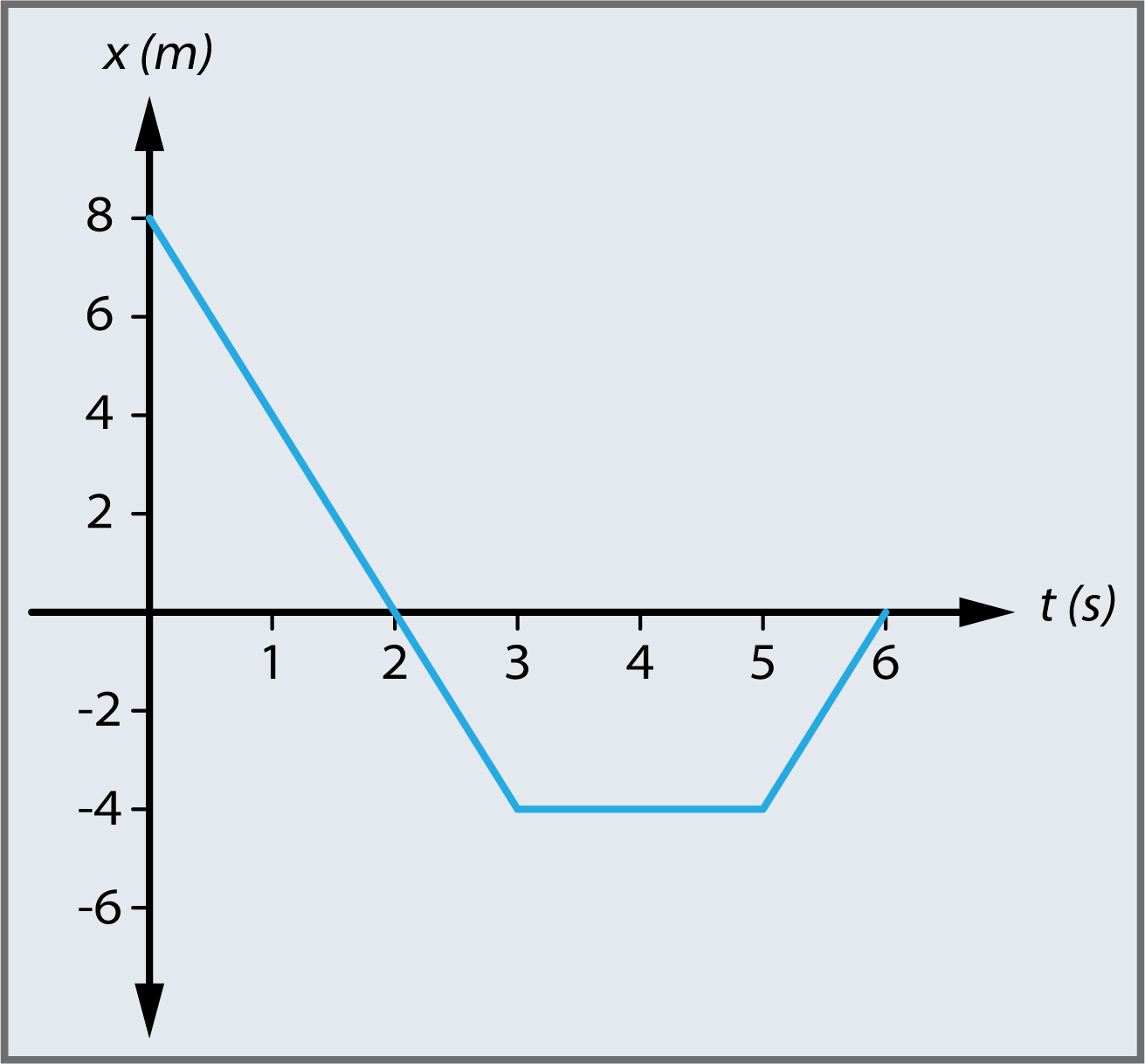
Déterminer les paramètres suivant pour ce dauphin :
La vitesse moyenne entre les instants \(t=0\,s\) et \(t=6\,s\).
La vitesse scalaire moyenne entre les instants \(t=0\,s\) et \(t=6\,s\).
La vitesse instantanée à l’instant \(t=1\,s\).
La vitesse scalaire instantanée à l’instant \(t=4\,s\).
solution
La vitesse moyenne est définie comme le déplacement sur le temps.
\[v_{moy}=\dfrac{\Delta x}{\Delta t}=\dfrac{x_{f}-x_{0}}{t_{f}-t_{0}}=\dfrac{0\,m-8\,m}{6\,s-0\,s}=\dfrac{-8\,m}{6\,s}\]On fait le calcul et on précise les unités : \(v_{moy}=-\dfrac{4\,m}{3\,s}=-1.33\,m/s\)
La vitesse scalaire moyenne est définie comme la distance totale parcourue sur le temps. Cette distance est la somme de toutes les longueurs des segments qui constituent le trajet total du dauphin.
Entre les instants \(t=0\,s\) et \(t=3\,s\), le dauphin a nagé sur une distance de \(12\) mètres puisqu’il est passé de \(x=8\,m\) à \(x=-4\,m\).
Puis, entre les instants \(t=3\,s\) et \(t=5\,s\), il a nagé sur une distance de \(0\) mètres puisqu’il est resté en \(x=-4\,m\) sans bouger.
Enfin, entre les instants \(t=5\,s\) et \(t=6\,s\), il a nagé sur une distance de \(4\) mètres puisqu’il est passé de \(x=-4\,m\) à \(x=0\,m\).
On utilise la définition de la vitesse scalaire moyenne:\[v_{scal\,moy}=\dfrac{\text{distance totale parcoure}}{\Delta t}=\dfrac{12\,m+0\,m+4\,m}{6\,s-0\,s}=\dfrac{16\,m}{6\,s}\]On fait le calcul et on précise les unités : \(v_{scal\,moy}=\dfrac{8\,m}{3\,s}=2.67\,m/s\)
La vitesse instantanée est égale à la pente de la courbe à cet instant. Pour déterminer la pente à l’instant \(t=1\,s\), on choisit deux points de la courbe entre les instants \(t=0\,s\) et \(t=3\,s\)(la pente ne change pas entre ces instants). Par exemple, en choisissant les instants \(t=2\,s\) et \(t=0\,s\), on calcule la pente de la manière suivante :
La vitesse scalaire instantanée est égale à la valeur absolue de la pente de la courbe à cet instant. A l’instant \(t=4\,s\) la pente est nulle, la vitesse instantanée à l’instant \(t=4\,s\) est donc aussi nulle.
