9.6. La 3^ème loi de Newton

La symétrie des forces

Il y a un passage dans la comédie musicale l’Homme de la Mancha qui se rapporte à la troisième loi du mouvement de Newton. Sancho, en décrivant une bagarre avec sa femme à Don Quichotte, dit: “Bien sûr, je l’ai frappée en arrière, Votre Grâce, mais elle est beaucoup plus dure que moi et vous savez ce qu’ils disent: “Que la pierre touche le lanceur ou le lanceur frappe la pierre, ça va être mauvais pour le lanceur”.” C’est exactement ce qui se passe chaque fois qu’un corps exerce une force sur un autre - le premier subit également une force (égale en amplitude et en sens inverse). De nombreuses expériences courantes, telles que se cogner un orteil ou lancer une balle, le confirment. C’est précisément indiqué dans la troisième loi du mouvement de Newton.

Troisième loi de Newton

Chaque fois qu’un corps exerce une force sur un second corps, le premier corps subit une force de grandeur égale et de direction opposée à la force qu’il exerce.

\[\vec{F}_{1\,sur\,2}=-\vec{F}_{2\,sur\,1}\]

Cette loi représente une certaine symétrie dans la nature : les forces se produisent toujours par paires, et un corps ne peut pas exercer une force sur un autre sans éprouver une force elle-même. Nous appelons parfois cette loi vaguement action-réaction, où la force exercée est l’action et la force ressentie en conséquence est la réaction. La troisième loi de Newton a des utilisations pratiques pour analyser l’origine des forces et comprendre quelles forces sont extérieures à un système.

Nous pouvons facilement voir la troisième loi de Newton à l’œuvre en regardant comment les gens se déplacent. Prenons l’exemple d’un nageur poussant du côté d’une piscine, comme illustré à la Fig. 9.8. Elle pousse contre le mur de la piscine avec ses pieds et accélère dans le sens opposé à celui de sa poussée. Le mur a exercé une force égale et opposée sur le nageur. Vous pourriez penser que deux forces égales et opposées s’annuleraient, mais ce n’est pas le cas parce qu’elles agissent sur des systèmes différents . Dans ce cas, il y a deux systèmes que nous pourrions étudier : le nageur ou le mur. Si nous choisissons le nageur comme système d’intérêt, comme sur la figure, alors \(\vec{F}_{mur\,sur\,pieds}\) est une force externe sur ce système et affecte son mouvement. Le nageur se déplace dans la direction de \(\vec{F}_{mur\,sur\,pieds}\). En revanche, la force \(\vec{F}_{pieds\,sur\,mur}\) agit sur le mur et non sur notre système d’intérêt. Donc \(\vec{F}_{pieds\,sur\,mur}\) n’affecte pas directement le mouvement du système et n’annule pas \(\vec{F}_{mur\,sur\,pieds}\). Notez que la nageuse pousse dans la direction opposée à celle dans laquelle elle souhaite se déplacer. La réaction à sa poussée est donc dans la direction souhaitée.

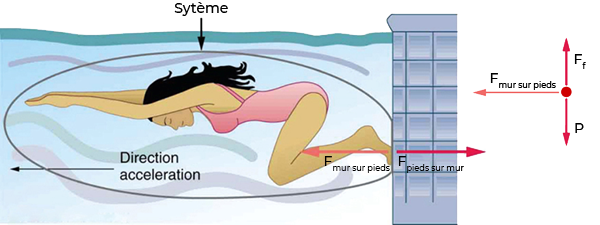
Fig. 9.8 Lorsque le nageur exerce une force \(\vec{F}_{pieds\,sur\,mur}\) sur le mur, elle accélère dans le sens opposé à celui de sa poussée. Cela signifie que la force externe résultante exercée sur elle est dans la direction opposée à \(\vec{F}_{pieds\,sur\,mur}\). Cette opposition se produit parce que, conformément à la troisième loi du mouvement de Newton, le mur exerce une force \(\vec{F}_{mur\,sur\,pieds}\) sur elle, de grandeur égale mais dans le sens opposé à celui qu’elle exerce sur elle. La ligne autour du nageur indique le système d’intérêt. Notez que \(\vec{F}_{pieds\,sur\,mur}\) n’agit pas sur ce système (le nageur) et, par conséquent, n’annule pas \(\vec{F}_{mur\,sur\,pieds}\). Ainsi, le diagramme du corps libre montre seulement \(\vec{F}_{mur\,sur\,pieds}\), la force gravitationnelle, et \(\vec{F}_{f}\), la force de flottabilité de l’eau supportant le poids du nageur. Les forces verticales \(\vec{P}\) et \(\vec{F}_{f}\) s’annulent car il n’y a pas de mouvement vertical. (crédit : openstax.org)

D’autres exemples de la troisième loi de Newton sont faciles à trouver. Alors qu’un professeur fait les cent pas devant un tableau blanc, elle exerce une force vers l’arrière sur le sol. Le sol exerce une force de réaction vers l’avant sur le professeur qui la fait accélérer vers l’avant. De même, une voiture accélère parce que le sol pousse vers l’avant sur les roues motrices en réaction aux roues motrices qui poussent vers l’arrière sur le sol. Vous pouvez voir des preuves que les roues poussent vers l’arrière lorsque les pneus patinent sur une route de gravier et projettent des pierres en arrière. Dans un autre exemple, les fusées avancent en expulsant du gaz vers l’arrière à grande vitesse. Cela signifie que la fusée exerce une grande force vers l’arrière sur le gaz dans la chambre de combustion de la fusée, et que le gaz exerce donc une grande force de réaction vers l’avant sur la fusée. Cette force de réaction est appelée poussée. C’est une idée fausse courante que les fusées se propulsent en poussant sur le sol ou dans les airs derrière elles. Ils fonctionnent mieux dans le vide, où ils peuvent plus facilement expulser les gaz d’échappement. Les hélicoptères créent de la même manière une portance en poussant l’air vers le bas, subissant ainsi une force de réaction ascendante. Les oiseaux et les avions volent également en exerçant une force sur l’air dans une direction opposée à celle de la force dont ils ont besoin. Par exemple, les ailes d’un oiseau poussent l’air vers le bas et vers l’arrière afin de se soulever et d’avancer. Une pieuvre se propulse dans l’eau en éjectant de l’eau à travers un entonnoir de son corps, semblable à un jet ski. Dans une situation similaire à celle de Sancho, les combattants professionnels en cage subissent des forces de réaction lorsqu’ils frappent, se cassant parfois la main en frappant le corps d’un adversaire.

Exemple : Choisir le bon système

Une professeure de physique pousse un chariot d’équipement de démonstration dans une salle de conférence, comme le montre la figure ci-dessous. Sa masse est de \(65.0\,kg\), celle du chariot de \(12.0\,kg\) et celle de son équipement de \(7.0\,kg\). Calculez l’accélération produite lorsque la professeure exerce une force vers l’arrière de \(150\,N\) sur le sol. Toutes les forces opposées au mouvement, telles que la friction sur les roues du chariot et la résistance à l’air, totalisent \(24.0\,N\).

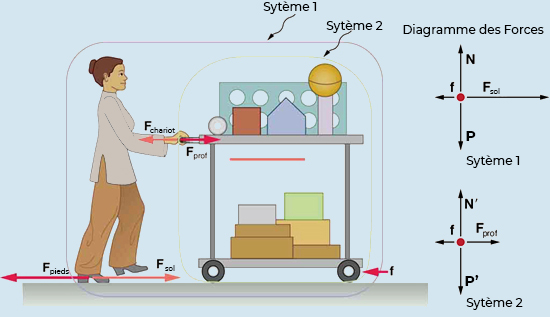
Fig. 9.9 Une professeure pousse un chariot d’équipement de démonstration. Les longueurs des flèches sont proportionnelles à l’amplitude des forces (sauf pour \(\vec{f}\), car elle est trop petite pour être dessinée à l’échelle). Différentes questions sont posées dans chaque exemple; ainsi, le système doit être défini différemment pour chacun. Le système 1 est approprié pour cet exemple, car il demande l’accélération de l’ensemble du groupe d’objets. Seulement \(\vec{F}_{sol}\) et \(\vec{f}\) sont des forces externes agissant sur le système 1 le long de la ligne de mouvement. Toutes les autres forces annulent ou agissent sur le monde extérieur. Le système 2 est choisi pour l’ exemple afin que \(\vec{F}_{prof}\) sera une force extérieure et entrera dans la deuxième loi de Newton. Notez que les diagrammes des forces, qui nous permettent d’appliquer la deuxième loi de Newton, varient selon le système choisi. (crédit : openstax.org)

stratégie

Puisqu’ils accélèrent en tant qu’unité, nous définissons le système comme étant la professeure, le chariot et l’équipement.

Il s’agit du système 1 de la figure ci-dessus. La professeure recule avec force \(\vec{F}_{pieds}\) de \(150\,N\). Selon la troisième loi de Newton, le sol exerce une force de réaction vers l’avant \(\vec{F}_{sol}\) de \(150\,N\) sur le système 1. Puisque tout mouvement est horizontal, nous pouvons supposer qu’il n’y a pas de force résultante dans la direction verticale.

Le problème est donc unidimensionnel le long de la direction horizontale. Comme indiqué, \(\vec{f}\) s’oppose au mouvement et est donc dans la direction opposée de \(\vec{F}_{sol}\). Notez que nous n’incluons pas les forces \(\vec{F}_{prof}\) ou \(\vec{F}_{chariot}\) car ce sont des forces internes, et nous n’incluons pas \(\vec{F}_{pieds}\) car il agit sur le sol, pas sur le système. Il n’y a pas d’autres forces significatives agissant sur le système 1. Si la force externe résultante peut être trouvée à partir de toutes ces informations, nous pouvons utiliser la deuxième loi de Newton pour trouver l’accélération comme demandé (Voir le diagramme des forces sur la figure).

solution

La deuxième loi de Newton est donnée par

\[a=\dfrac{F_{res}}{m}\]

La force externe résultante sur le système 1 est déduite de la figure ci-dessus et de la discussion ci-dessus comme étant

\[F_{res}=\Sigma F=F_{sol}-f=150\,N-24,0\,N=126\,N\]

La masse du système 1 est

\[m=(65,0+12,0+7,0)\,kg=84\,kg\]

Ces valeurs produisent une accélération de

\[a=\dfrac{F_{res}}{m}=\dfrac{126\,N}{84\,kg}=1,5\,m/s^{2}\]

discussion

Aucune des forces entre les composants du système 1, comme entre les mains de la professeure et le chariot, ne contribue à la force externe résultante car elles sont internes au système 1.
Une autre façon de voir cela est de noter que les forces entre les composants d’un système annulez parce qu’ils sont égaux en grandeur et de sens opposé. Par exemple, la force exercée par la professeure sur le chariot se traduit par une force égale et opposée sur elle. Dans ce cas, les deux forces agissent sur le même système et, par conséquent, s’annulent. Ainsi, les forces internes (entre les composants d’un système) s’annulent. Le choix du système 1 était crucial pour résoudre ce problème.

Exemple : Force sur le chariot - Choix d’un nouveau système

Calculez la force exercée par la professeure sur le chariot de la figure de l’exemple précédent en utilisant les mêmes données si nécessaire.

stratégie

Si nous définissons maintenant le système d’intérêt comme étant le chariot plus équipement (système 2 sur la figure ci-dessus), alors la force externe résultante sur le système 2 est la force exercée par la professeure sur le chariot moins la friction.

La force qu’elle exerce sur le chariot,\(\vec{F}_{prof}\), est une force externe agissant sur le système 2. \(\vec{F}_{prof}\) était interne au système 1, mais il est externe au système 2 et entrera dans la deuxième loi de Newton pour le système 2.

solution

La deuxième loi de Newton peut être utilisée pour trouver \(\vec{F}_{prof}\). Commençant par

\[a=\dfrac{F_{res}}{m}\]

et notant que l’amplitude de la force externe résultante sur le système 2 est

\[F_{res}=\Sigma F=F_{prof}-f\]

nous résolvons pour \(\vec{F}_{prof}\), la quantité souhaitée:

\[F_{prof}=F_{res}+f\]

La valeur de \(\vec{f}\) est donnée, il faut donc calculer le force résultante \(\vec{F}_{res}\). Cela peut être fait puisque l’accélération et la masse du système 2 sont connues. En utilisant la deuxième loi de Newton, nous voyons que

\[F_{res}=m\cdot a\]

où la masse du système 2 est de \(19,0\,kg\) (\(m=12,0\,kg+7,0\,kg\)) et son accélération s’est avérée être \(a=1,5\,m/s^{2}\) dans l’exemple précédent. Donc,

\[F_{res}=m\cdot a=19\,kg\cdot 1,5\,m/s^{2}=29\,N\]

Maintenant, nous pouvons trouver la force souhaitée:

\[F_{prof}=F_{res}+f=29\,N+24\,N=53\,N\]

discussion

Il est intéressant de noter que cette force est nettement inférieure à la force de \(150\,N\) que la professeure a exercée en arrière sur le sol. Toute cette force de \(150\,N\) n’est pas transmise au chariot; une partie accélère également masse de la professeure.

Le choix d’un système est une étape analytique importante à la fois dans la résolution de problèmes et dans la compréhension approfondie de la physique de la situation (ce qui n’est pas forcément la même chose).