5.1. Graphique de la position x(t)#
A quoi sert la courbe \(x(t)\) ?#
Pour beaucoup de gens, se retrouver face à une courbe sur un graphique, c’est un peu comme aller chez le dentiste: cela fait naître un vague sentiment d’inquiétude avec l’envie d’en finir au plus vite. Pourtant, la représentation graphique de la position en fonction du temps est un moyen efficace pour visualiser un grand nombre d’informations concernant le mouvement d’un objet.
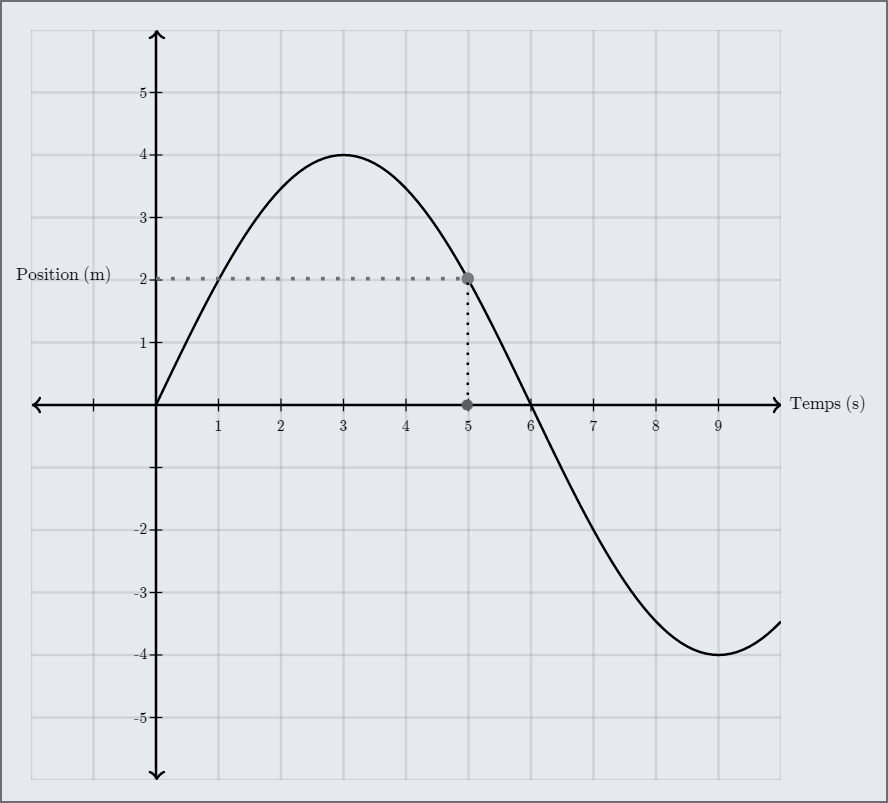
Fig. 5.1 Courbe de \(x(t)\). La position de l’objet à \(t=5\,s\) et de \(2\,m\). (crédit : khanacademy.org)#
L’axe vertical représente la position \(x\) d’un objet. Grâce à la courbe de la figure Fig. 5.1, on peut, par exemple, déterminer pour chaque instant (valeurs notées sous l’axe horizontal, en secondes) la position de l’objet considéré (valeurs notées à gauche de l’axe vertical, en mètres). Mais pas seulement.
Que représente la pente de la courbe \(x(t)\) ?#
La pente de la courbe \(x(t)\) correspond à la variation de position de l’objet. La valeur de cette pente est donc la valeur de la vitesse instantanée de l’objet. Pour mieux comprendre, on considère la courbe de \(x(t)\) suivante:
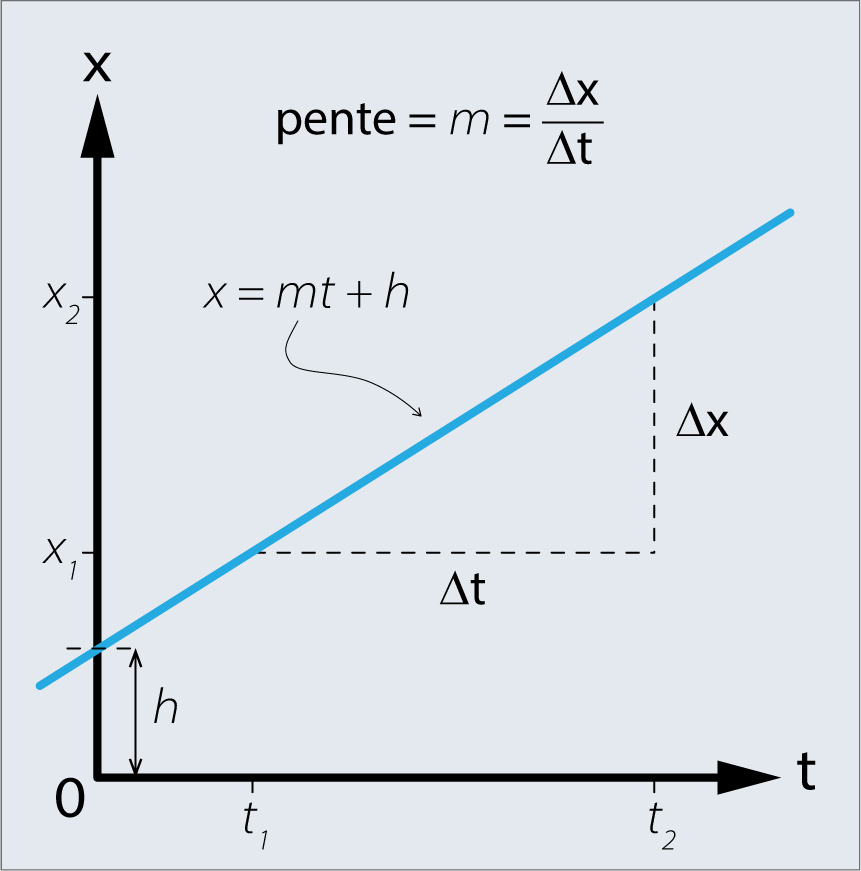
Fig. 5.2 La figure montre un graphique en ligne droite. L’équation de la ligne droite est \(x(t)=m\cdot t + h\), ou \(m\) est la pente de la droite et \(h\) sa position au temps \(t_{0}=0\).#
La pente de cette courbe est définie comme suit:
Cette expression de la pente est la même que celle de la vitesse:
A retenir !
\(\boldsymbol{\rightarrow}\quad\) La pente de la courbe de \(\boldsymbol{x(t)}\) correspond à la vitesse.
Cela est aussi vrai lorsque la pente de la courbe donnant \(x(t)\) varie. Sur l’exemple suivant, le trait rouge montre la pente à trois instants donnés.
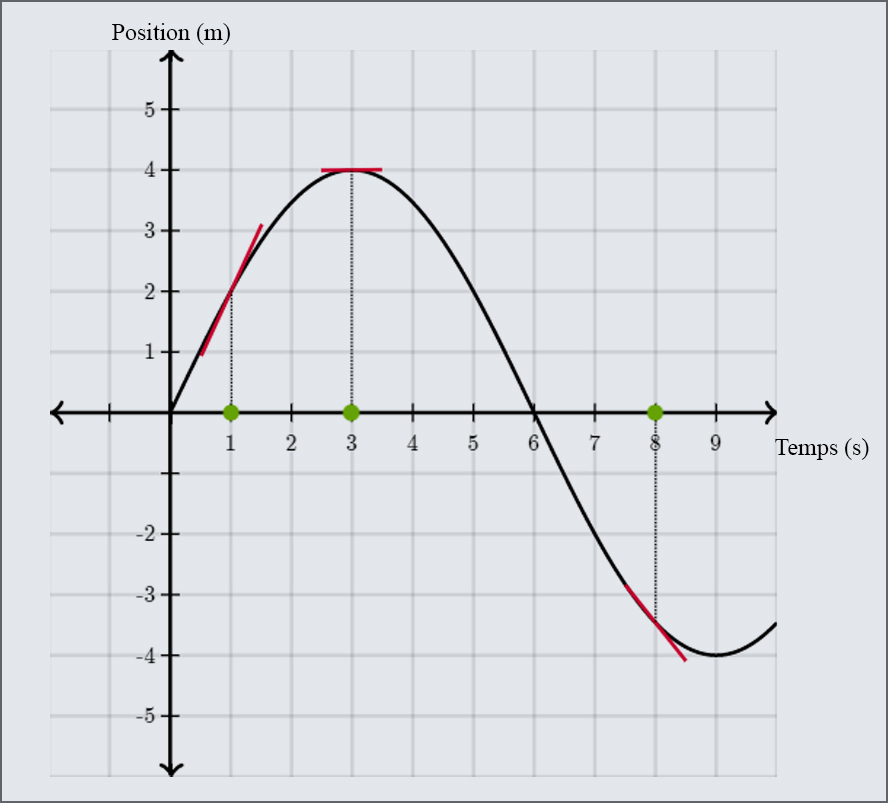
Fig. 5.3 La tangente du graphique donne la pente à un instant donné qui est égale à la vitesse instantanée de l’objet. (crédit : khanacademy.org)#
La pente de la courbe entre les instants \(t=0\,s\) et \(t=3\,s\) est positive puisque le trait rouge est dirigé vers le haut. Cela signifie que la vitesse est positive et ainsi que l’objet se déplace dans la direction positive.
La pente de la courbe entre les instants \(t=3\,s\) et \(t=9\,s\) est négative puisque le trait rouge est dirigé vers le bas. Cela signifie que la vitesse est négative et ainsi que l’objet se déplace dans la direction négative.
La pente de la courbe est nulle à l’instant \(t=3\,s\) puisque le trait rouge est horizontal. Cela signifie que la vitesse est nulle et ainsi que l’objet est momentanément au repos.
La vitesse peut être instantanée ou moyenne. Il est important de noter que la pente de la courbe de \(x(t)\) à un instant donné correspond à la vitesse instantanée. En revanche, la pente moyenne entre deux instants correspond à la vitesse moyenne entre ces deux instants. La vitesse instantanée n’est pas forcément égale à la vitesse moyenne. Par contre, si la pente est constante sur une certaine durée (c’est à dire si la courbe est un segment de droite sur cet intervalle de temps), alors la vitesse instantanée est égale à la vitesse moyenne.
A quoi correspond la courbure de la courbe \(x(t)\) ?#
On peut dire que la représentation graphique donnée à la Fig. 5.4 est courbée dans la mesure où elle n’est pas faite que de segments de droite. Cela signifie que la pente varie et donc que la vitesse varie elle aussi. Lorsque la vitesse varie, il y a une accélération. Par conséquent, si la courbe de \(x(t)\) est incurvée, c’est que l’objet accélère, ou encore que sa vitesse varie.
A retenir !
\(\boldsymbol{\rightarrow}\quad\) La courbure de la courbe de \(\boldsymbol{x(t)}\) correspond à l’accélération.
Il est possible de visualiser les changements de pente sur la Fig. 5.4. La première bosse, entre \(t=1\,s\) et \(t=5\,s\), représente une accélération négative puisque la pente passe d’une valeur positive (trait rouge dirigé vers le haut) à une valeur négative (trait rouge dirigé vers le bas). La seconde bosse, entre \(t=7\,s\) et \(t=11\,s\), représente une accélération positive puisque la pente passe d’une valeur négative à une valeur positive. Dans les deux cas le sens de l’accélération est opposée au sens de déplacement.
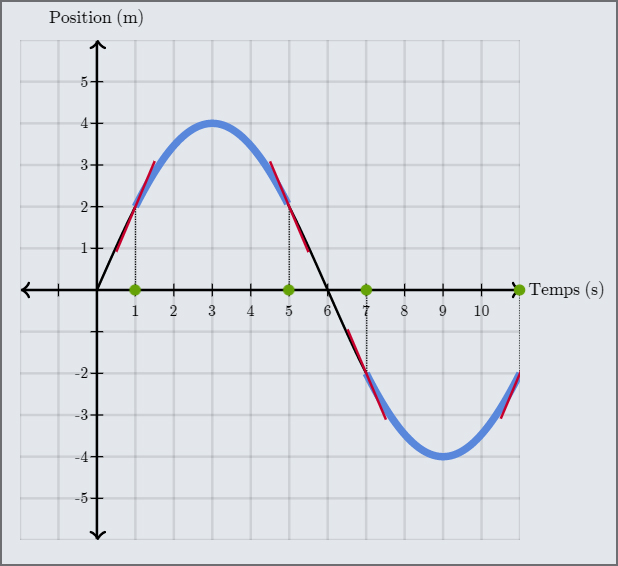
Fig. 5.4 Un changement dans le signe de la pente de la tangente (\(+/-\)) indique une accélération opposée au déplacement. (crédit : khanacademy.org)#
Pour résumer, si la courbe de \(x(t)\) ressemble à un bol à l’envers, l’accélération est négative. Et si elle ressemble à un bol à l’endroit, l’accélération est positive. Voici un moyen pour s’en rappeler: lorsque le bol est à l’envers, toute la nourriture qu’il contient tombe, ce qui est plutôt négatif. En revanche, lorsqu’il est à l’endroit, la nourriture y reste, ce qui est plutôt positif.
Exemple 1 : Le morse qui avait faim
Un morse se déplace horizontalement et fait des va-et-vient cherchant de la nourriture. Son mouvement est décrit ci-dessous par la représentation graphique de sa position horizontale \(x\) en fonction du temps \(t\).
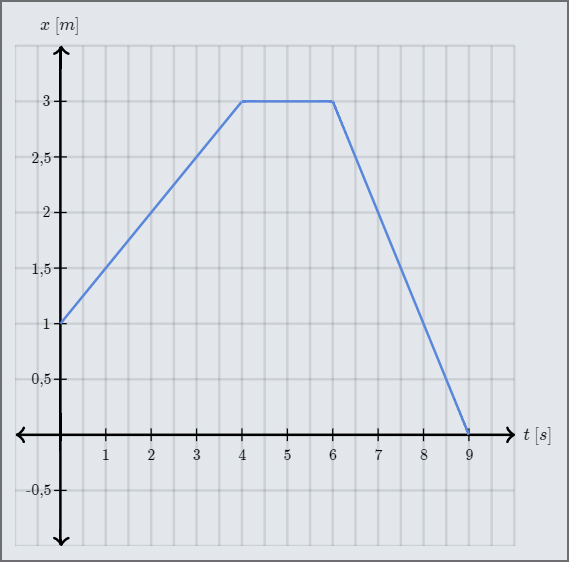
Que vaut la vitesse instantanée aux instants suivants: \(2\,s\), \(5\,s\) et \(8\,s\)?
solution
- Vitesse à \(\,t=2\,s\) :
On détermine la vitesse du morse à l’instant \(t =2\,s\) en calculant la pente de la courbe à cet instant:
On utilise la formule de la pente:
\[v=\text{pente}=\dfrac{x_{2}-x_{1}}{t_{2}-t_{1}}\]On choisit ensuite deux points faciles à repérer le long du segment de droite considéré. On prend par exemple les points (\(0\,s\); \(1\,m\)) et (\(4\,s\); \(3\,m\)), cependant d’autres points entre \(0\,s\) et \(4\,s\) pourraient convenir:
On fait l’application numérique et on précise les unités:
\[v=\text{pente}=\dfrac{3\,m-1\,m}{4\,s-0\,s}=\dfrac{2\,m}{4\,s}=\dfrac{1}{2}\,m/s\]La vitesse du morse à \(t=2\,s\) est donc de \(0.5\,m/s\).
- Vitesse à \(\,t=5\,s\) :
Pour déterminer la vitesse à \(t=5\,s\), il suffit de remarquer que la tangente à la courbe est horizontale à cet instant.
La pente est donc nulle, ce qui signifie que la vitesse du morse à \(t=5\,s\) est de \(0\,m/s\).- Vitesse à \(\,t=8\,s\) :
On utilise la formule de la pente:
\[v=\text{pente}=\dfrac{x_{2}-x_{1}}{t_{2}-t_{1}}\]On choisit les points des extrémités du segment de droite, à savoir les points (\(6\,s\); \(3\,m\))et (\(9\,s\); \(0\,m\))
On fait l’application numérique et on précise les unités:
\[ v=\text{pente}=\dfrac{0\,m-3\,m}{9\,s-6\,s}=\dfrac{-3\,m}{3\,s}=-1\,m/s\]La vitesse du morse à \(t=8\,s\) est donc de \(-1\,m/s\).
Exemple 2 : Vol d’un oiseau
La courbe ci-dessous montre le mouvement d’un oiseau, volant vers le bas puis vers le haut, dont le mouvement est représenté par sa position verticale \(y\) en fonction du temps \(t\).
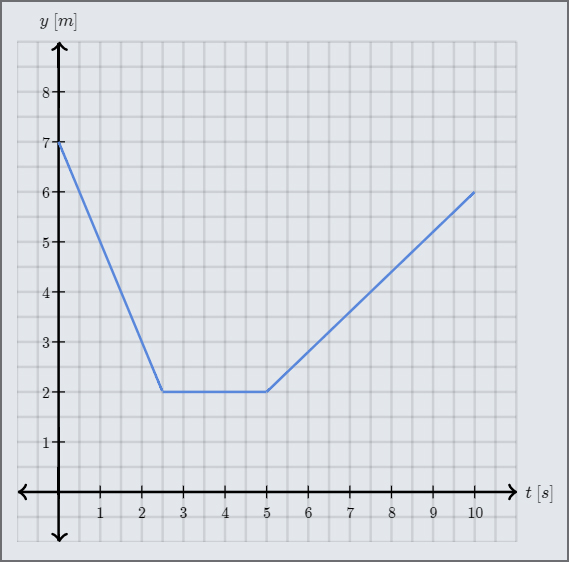
Quelle est la vitesse moyenne de l’oiseau entre les instants \(t=0\,s\) et \(t=10\,s\) ?
Quelle est la vitesse scalaire moyenne de l’oiseau entre les instants \(t=0\,s\) et \(t=10\,s\) ?
solution
- Vitesse moyenne entre les instants \(t=0\,s\) et \(t=10\,s\) :
On calcule la pente moyenne de la courbe entre ces deux instants. Graphiquement, cela revient à déterminer la pente du segment de droite qui relierait les deux extrémités de la courbe (en rouge).
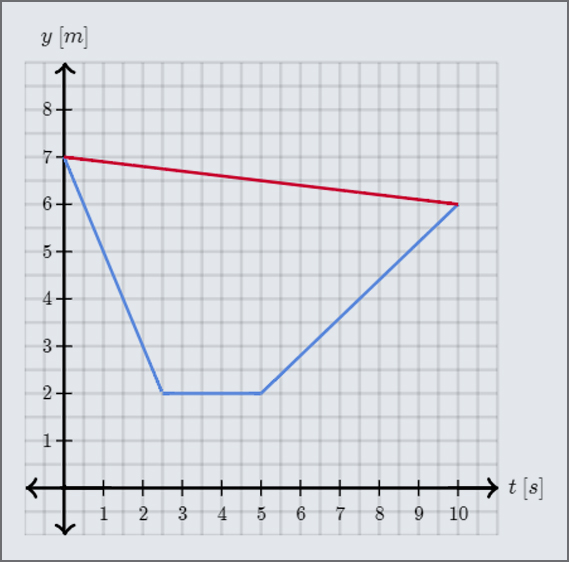
On utilise la formule de la pente:
\[v_{moy}=\text{pente}=\dfrac{x_{2}-x_{1}}{t_{2}-t_{1}}\]Les deux extrémités de la courbe correspondent au point de départ (\(0\,s\); \(7\,m\)) et au point d’arrivée (\(10\,s\); \(6\,m\)).
On fait l’application numérique et on précise les unités:
\[v_{moy}=\dfrac{6\,m-7\,m}{10\,s-0\,s}=\dfrac{-1\,m}{10\,s}=-0.1\,m/s\]La vitesse moyenne de l’oiseau entre les instants \(t=0\,s\) et \(t=10\,s\) est de \(-0.1\,m/s\).
- Vitesse scalaire moyenne entre les instants \(t=0\,s\) et \(t=10\,s\) :
Par définition, la vitesse scalaire moyenne est la distance totale parcourue divisée par l’intervalle de temps. Pour déterminer la distance totale parcourue, il suffit d’additionner les longueurs des différents déplacements du trajet:
Entre les instants \(t=0\,s\) et \(t=2.5\,s\), l’oiseau s’est déplacé de \(5\,m\) vers le bas.
Puis, entre les instants \(t=2.5\,s\) et \(t=5.0\,s\), l’oiseau n’a pas bougé.
Enfin, entre les instants \(t=5.0\,s\) et \(t=10\,s\), l’oiseau s’est déplacé de \(4,m\) vers le haut.
La distance totale parcourue est donc : \(\text{distance}=9\,m\).
On divise maintenant ce résultat par l’intervalle de temps pour obtenir la vitesse moyenne (on utilise la formule de la vitesse scalaire moyenne):
\[v_{scal\,moy}=\frac{\text{distance}}{\Delta t}\]On fait l’application numérique et on précise les unités:
\[v_{scal\,moy}=\frac{\text{9\,m}}{10\,s}=\dfrac{9}{10}\,m/s=0.9\,m/s\]La vitesse scalaire moyenne de l’oiseau entre les instants \(t=0\,s\) et \(t=10\,s\) est de \(0.9\,m/s\).
