2.2. Systèmes de coordonnées

2.2.1. Mouvements à une dimension

Afin de décrire une grandeur vectorielle, il faut d’abord définir une direction positive.
Pour cela, vous devez dessiner un système de coordonnées ou un système d’axes de référence. Pour un mouvement à 1 dimension, (unidimensionnel ou unidirectionnel), il s’agit simplement d’un axe (souvent noté axe x).

En général, lorsqu’un objet à un mouvement horizontal, le déplacement vers la droite est considéré comme positif et le déplacement vers la gauche est considéré comme négatif.
Avec un mouvement vertical, le déplacement vers le haut est généralement positif et le mouvement vers le bas est négatif.

Dans certains cas, il peut cependant être plus pratique de changer les directions positive et négative. Par exemple, si vous analysez le mouvement d’un objet qui tombe, il peut être utile de définir le bas comme la direction positive. Si des personnes dans une course courent vers la gauche, il est utile de définir la gauche comme la direction positive.
Cela n’a pas d’importance tant que les axes sont clairs et cohérents. Une fois que vous avez attribué une direction positive et que vous commencez à résoudre le problème, vous ne pouvez plus la changer.

Fig. 2.4 On considére souvent les directions vers le haut ou vers la droite comme positives (\(+\)) et les directions vers le bas ou vers la gauche comme négatives (\(-\)).

2.2.2. Mouvements à deux et trois dimensions

Dans ce chapitre, nous allons nous intéresser uniquement au mouvement des objets à une dimension; donc au mouvement des objets le long d’une ligne droite, le long d’un seul axe. Cette restriction peut sembler à priori extrême, puisque la plupart des mouvements se passent sur des trajectoires curvilignes (ou quelconque) à deux ou trois dimensions.

Ce n’est pourtant pas le cas pour deux raisons:

1. Une courbe peut toujours être découpée et approximée en petit segment rectiligne. Plus le découpage sera fin, plus l’approximation de la courbe sera précise.
   Sur la Fig. 2.5, la trajectoire réelle d’un objet (en traitillé) peut être approximée par un (ou plusieurs) mouvement rectiligne. Plus le découpage de la trajectoire est important plus la succession des petits mouvements rectilignes se rapprochera de la trajectoire réelle. En bleu, il n’y a aucun découpage, l’approximation est grossière. En rose, le mouvement a été découpé en deux parties rectiligne. On gagne de l’information sur la trajectoire réelle. En Violet, le mouvement est découpé en quarte parties rectiligne. On se rapproche de la courbe de la trajectoire. Finalement, en vert, le mouvement est découpé en huit parties rectilignes qui sont une bonne approximation de la courbe réelle.

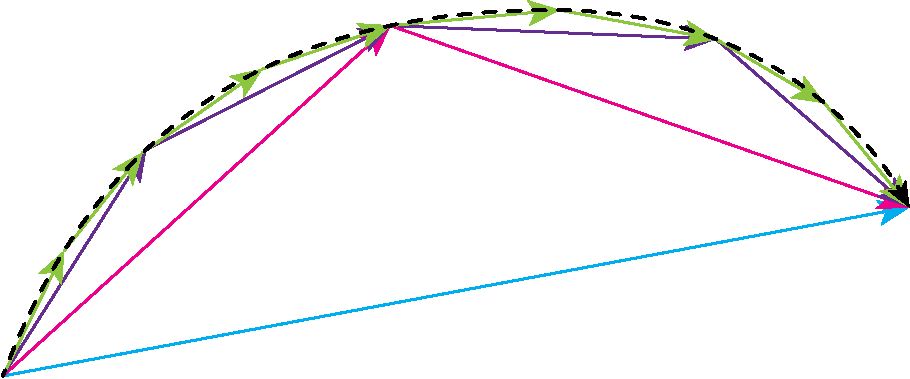
Fig. 2.5 En bleu: Le mouvement rectiligne est assez éloigné de la trajectoire réelle. En rose et violet: deux autre découpage plus ou moins précis. En vert: La suite des mouvements rectilignes se rapproche de la trajectoire réelle.

2. A cause de l’indépendance des mouvements perpendiculaires. Dans un mouvement à 2 (ou 3) dimensions, ce qui se passe le long de l’axe des \(x\) est indépendant de ce qui se passe le long de l’axe des \(y\) (ou/et \(z\)). Les composantes horizontale et verticale du mouvement bidimensionnel sont indépendantes l’une de l’autre. Tout mouvement dans la direction horizontale n’affecte pas le mouvement dans la direction verticale et vice versa.
   Ceci nous permet de décomposer les problèmes à deux (ou trois) dimensions en deux (ou trois) problèmes à une dimension, comme le montre l’exemple ci-dessous.
   Pour résoudre un problème à plusieurs dimensions, il suffira donc de décomposer le problème initial en plusieurs sous-problème, à une dimension chacun. On résout ensuite chaque sous-problème à une dimension de manière indépendante (attention, le temps \(t\) est cependant identique pour chaque sous-problème), puis on recombine le tout pour trouver la solution finale du problème.

On analysera les mouvements à deux dimension plus en détail dans la leçon sur le []{chap:mvt2D}.

Décomposition d’un mouvement à deux dimensions

Supposons qu’un piéton marche d’un point à un autre dans une ville avec des blocs carrés uniformes, comme illustré à la figure ci-dessous. Illustrons le problème avec des axes Nord/Sud-Est/Ouest comme repère (référentiel terrestre).

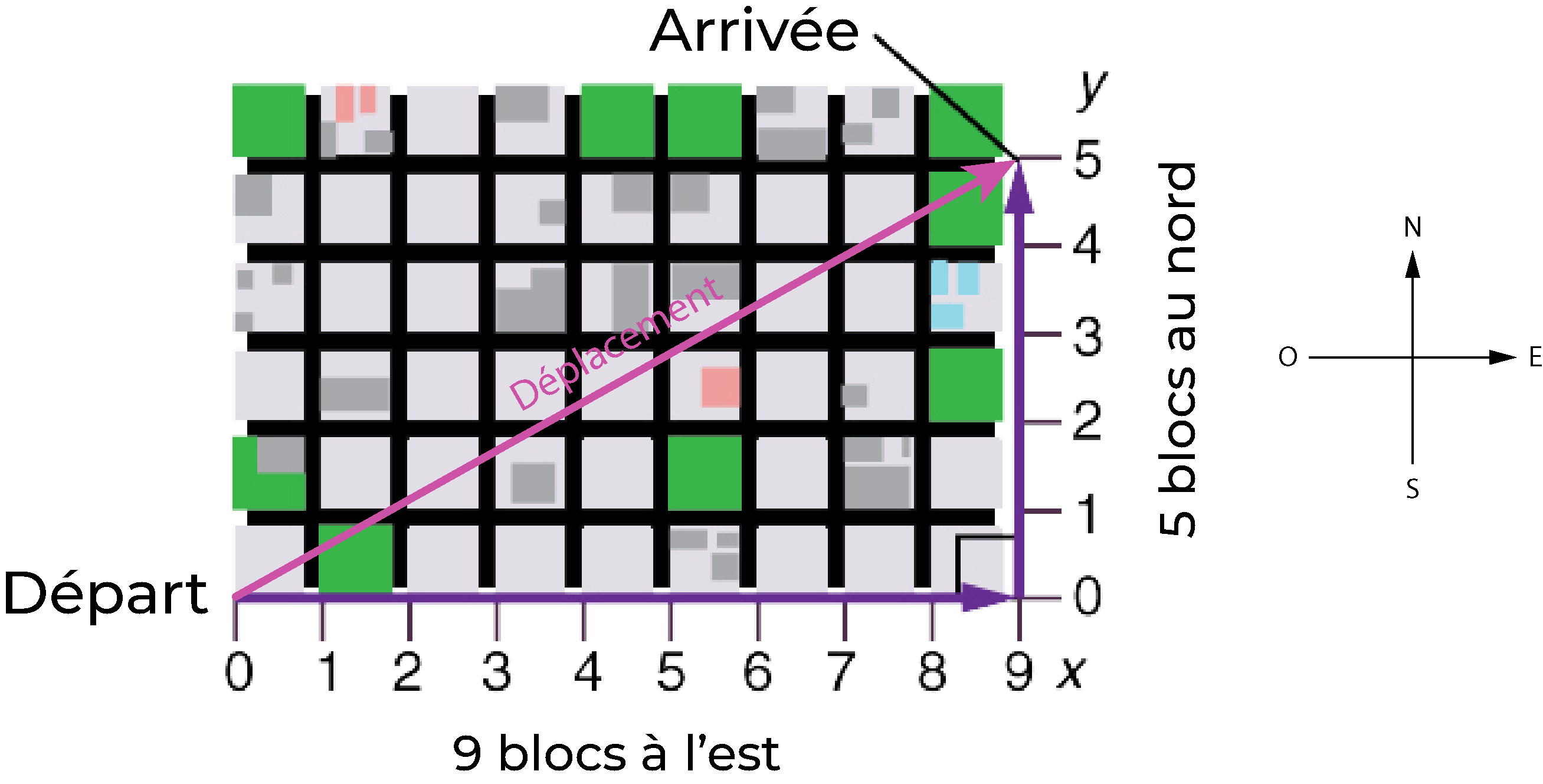
Fig. 2.6 Un piéton parcourt un chemin bidimensionnel entre deux points d’une ville. Dans cette ville, tous les blocs sont carrés et ont la même taille.

Pour analyser le mouvement du piéton, on considère uniquement le point de départ et le point d’arrivée. Dans cet exemple, le piéton ne peut pas prendre le chemin en ligne droite, car il est bloqué par les maison. Il se déplace soit selon l’axe Est/Ouest, soit selon l’axe Nord/Sud.

Si on veut décrire le mouvement du piéton, dans le repère Nord/Sud-Est/Ouest, on dira qu’il s’est déplacé de 9 blocs à l’est, suivi de 5 blocs au nord. Il marche vers l’est puis vers le nord (deux directions perpendiculaires). La distance parcourue vers l’est est affectée uniquement par son mouvement vers l’est. De même, la distance parcourue vers le nord n’est affectée que par son mouvement vers le nord.

En décrivant le déplacement de cette façon, on va décomposer le problème initial (à deux dimensions) en deux problèmes à une dimension. Un problème qui analyse uniquement le déplacement sur l’axe Est/Ouest et un autre problème uniquement le déplacement sur l’axe Nord/Sud.

Pour décomposer un vecteur (et donc le problème), il suffira de connaître les composantes de ce vecteur dans le système d’axe proposé. Pour cela le théorème de Pythagore et des notions de trigonométrie de base seront nécessaire. Dans la Fig. 2.7, les composantes du vecteur \(\vec{r}\) sont :

(2.1)\[\begin{split}\overrightarrow{r}= \begin{pmatrix} r_{x}\\ r_{y} \end{pmatrix}= \begin{pmatrix} r\cos(\alpha)\\ r\sin(\alpha) \end{pmatrix}\end{split}\]

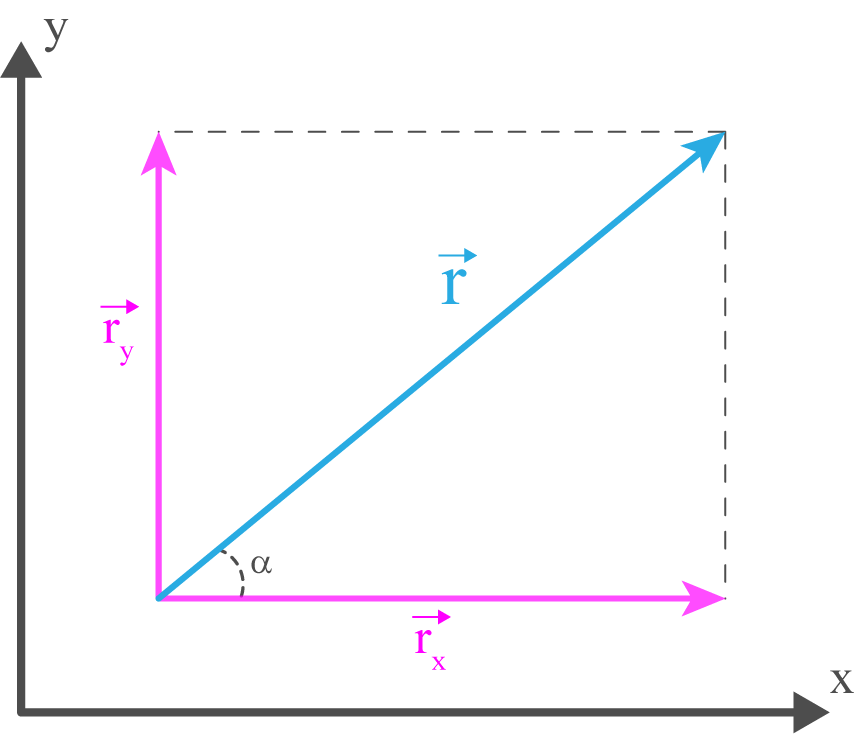
Fig. 2.7 Le vecteur \(\vec{r}\) est décomposé en \(r_{x}\) et \(r_{y}\) par trigonométrie.