1.3. Unités de mesure#
Les physiciens, comme d’autres scientifiques, font des observations et posent des questions fondamentales.
Par exemple, quelle est la taille d’un objet ? Quelle masse possède-t-il ? Quelle distance a-t-il parcourue ?
Pour répondre à ces questions, ils effectuent des mesures avec divers instruments (par exemple, mètre ruban, balance, chronomètre, etc.).
La physique est une science quantitative. Les mesures es quantités physique correspondent à différentes grandeurs, comme une longueur, un temps, une température,… Afin de les identifier, nous devons associer, à chaque mesure, une unité.
Par exemple, \(33\) ne suffit pas pour exprimer la vitesse d’une voiture, il faut également son unité :
\(33\,km/h\) correspond à la vitesse d’une voiture en ville.
\(33\,m/s\) correspond à la vitesse d’une voiture sur autoroute.
Sans unités, il serait extrêmement difficile pour les scientifiques d’exprimer et de comparer des valeurs mesurées de manière significative.
Système International d’unités#
Pour mesurer le monde qui nous entoure, nous avons besoin que de sept unités (Table 1.1). Ces unités de base du Système International d’unités (SI) sont les sept unités fondamentales à partir desquelles sont obtenues, par combinaison, toutes les autres unités en sciences (unités dérivées). Ces sept unités sont supposées indépendantes car elles permettent de mesurer des grandeurs physiques indépendantes.
Grandeur physique |
Notation |
Unité de base |
Symbole |
|---|---|---|---|
Distance |
\(x\), \(\Delta\)\(x\), \(d\), \(h\), \(l\) |
mètre |
\([m]\) |
Temps |
\(t\), \(\Delta\)\(t\) |
seconde |
\([s]\) |
Masse |
\(m\), \(M\) |
kilogramme |
\([kg]\) |
Courant électrique |
\(i\), \(I\) |
ampère |
\([A]\) |
Température |
\(T\) |
kelvin |
\([K]\) |
Quantité de matière |
\(n\) |
mole |
\([mol]\) |
Intensité lumineuse |
\(I\) |
candela |
\([cd]\) |
Lors d’une prise de mesure, ou pour communiquer un résultat, on peut utiliser l’unité que l’on souhaite, celle qui nous semble la plus adéquate. Par contre, chaque fois qu’une grandeur est utilisée dans une formule physique, il faut impérativement utiliser l’unité de base de cette grandeur physique. Cette unité est reconnue internationalement par le système international d’unité (SI).
La Table 1.2 ci-dessous présente toutes les grandeurs physiques qui seront utilisées dans le cours de cette année ainsi que leur unité de référence.
Grandeur physique |
Notation |
Unité de base |
Symbole |
Autres unités |
|---|---|---|---|---|
Distance |
\(x\), \(\Delta\)\(x\), \(d\) |
mètre |
\(\boldsymbol{[m]}\) |
\([km]\), \([cm]\), \([mm]\), \([\mu m]\) |
Temps |
\(t\), \(\Delta\)\(t\) |
seconde |
\(\boldsymbol{[s]}\) |
\([min]\); \([h]\) |
Masse |
\(m\), \(M\) |
kilogramme |
\(\boldsymbol{[kg]}\) |
\([g]\); \([mg]\); \([\mu g]\) |
Surface |
\(S\), \(A\) |
mètre carré |
\([m^{2}]\) |
\([cm^{2}]\); \([mm^{2}]\) |
Vitesse |
\(v\) |
mètre par seconde |
\([m/s]\) |
\([km/h]\), année-lumière |
Accélération |
\(a\) |
mètre par seconde au carré |
\([m/s^{2}]\) |
aucune ! |
Force |
\(F\) |
Newton |
\([N]\) |
\([kN]\), \([mN]\) |
Énergie |
\(E\) |
Joule |
\([J]\) |
\([MJ]\); \([kJ]\); \([Cal]\) |
Puissance |
\(P\) |
Watt |
\([W]\) |
\([GW]\); \([MW]\); \([kW]\) |
Attention
Mathématiquement, deux quantités sont égales si elles ont la même valeur : \(2+3=5\).
Physiquement, deux quantités sont égales si elles ont la même valeur et la même unité :
\(2\,m+3\,m=5\,m\), mais \(2\,m+3\,cm\neq 5\,m\) et encore moins \(2\,m+3\,kg=\,???\).
Lorsque deux grandeurs physique représentent la même quantité, mais avec des unités différentes, on parlera d’équivalence et non d’égalité. On utilisera de préférence le signe \(\equiv\)
Par exemple : \(1\) litre d’eau \(\equiv 1\,kg\).
Définition des unités de temps, de longueur et de masse#
Unité de temps#
L’unité SI pour le temps, la seconde (abrégé \(s\)), a une longue histoire.
Pendant de nombreuses années, elle a été définie comme \(1/86'400\) d’un jour solaire moyen. Plus récemment, une nouvelle norme a été adoptée pour gagner en précision et définir la seconde en termes de phénomène physique constant (car la journée solaire s’allonge en raison du ralentissement très progressif de la rotation de la Terre).
Les atomes de césium peuvent être amenés à vibrer d’une manière très régulière, et ces vibrations peuvent être facilement observées et comptées. En 1967, la seconde a été redéfinie comme le temps requis pour \(9'192'631'770\) de ces vibrations.
La précision des unités fondamentales est essentielle, car toutes les mesures sont finalement exprimées en termes d’unités fondamentales et ne peuvent être plus précises que les unités fondamentales elles-mêmes.
Unité de longueur#
L’unité SI pour la longueur est le mètre (abrégé \(m\)).
Sa définition a également changé au fil du temps pour devenir de plus en plus précise. Le mètre a été défini pour la première fois en 1791 comme \(1/10'000'000\) de la distance entre l’équateur et le pôle Nord. Cette mesure a été améliorée en 1889 en redéfinissant le mètre pour être la distance entre deux lignes gravées sur une barre de platine-iridium maintenant conservée près de Paris. En 1960, il était devenu possible de définir le mètre avec encore plus de précision en termes de longueur d’onde de la lumière, il a donc été redéfini à \(1'650'763.73\) longueurs d’onde de lumière orange émise par les atomes de krypton.
En 1983, le mètre a reçu sa définition actuelle (en partie pour une plus grande précision) par la distance parcourue par la lumière dans le vide en \(1/299'792'458\) de seconde. Ce changement définit la vitesse de la lumière à exactement \(299'792'458\) mètres par seconde. La longueur du mètre changera si la vitesse de la lumière est un jour mesurée avec une plus grande précision.
Unité de masse#
L’unité SI pour la masse est le kilogramme (abrégé \(kg\)).
Il était précédemment défini comme étant la masse d’un cylindre en platine-iridium conservé avec l’ancien étalon du compteur au Bureau international des poids et mesures près de Paris. Des répliques exactes du kilogramme précédemment définie sont également conservées au bureau international des poids et mesures (BIPM) à Paris, et à d’autres endroits dans le monde. La détermination de toutes les autres masses pourrait être finalement attribuée à une comparaison avec la masse standard. Même si le cylindre en platine-iridium était résistant à la corrosion, les contaminants en suspension dans l’air ont pu adhérer à sa surface, modifiant légèrement sa masse au fil du temps.
En mai 2019, la communauté scientifique a adopté une définition plus stable du kilogramme. Le kilogramme est maintenant défini en fonction de la seconde, du mètre et de \(h\), la constante de Planck (une valeur de la mécanique quantique qui relie l’énergie d’un photon à sa fréquence).
Les autres unités fondamentales, pour le courant électrique (l’ampère) ou la température (le kelvin), seront présentées l’année prochaine. Les premiers chapitres de ce cours portent sur la mécanique. Pour ce sujet, toutes les grandeurs physiques mesurées peuvent être exprimées en termes d’unités fondamentales de longueur, de masse et de temps.
Pour plus d’informations
Le site du réseau national de métrologie fournit une définition précise des autres unités de bases :
Sous-unités (multiples et sous-multiples)#
Pour chaque unité de mesure, on dispose de sous-unités afin d’exprimer des grandeurs plus grandes ou plus petites. On écrira ces sous-unités à l’aide d’un préfixe placé devant l’unité.
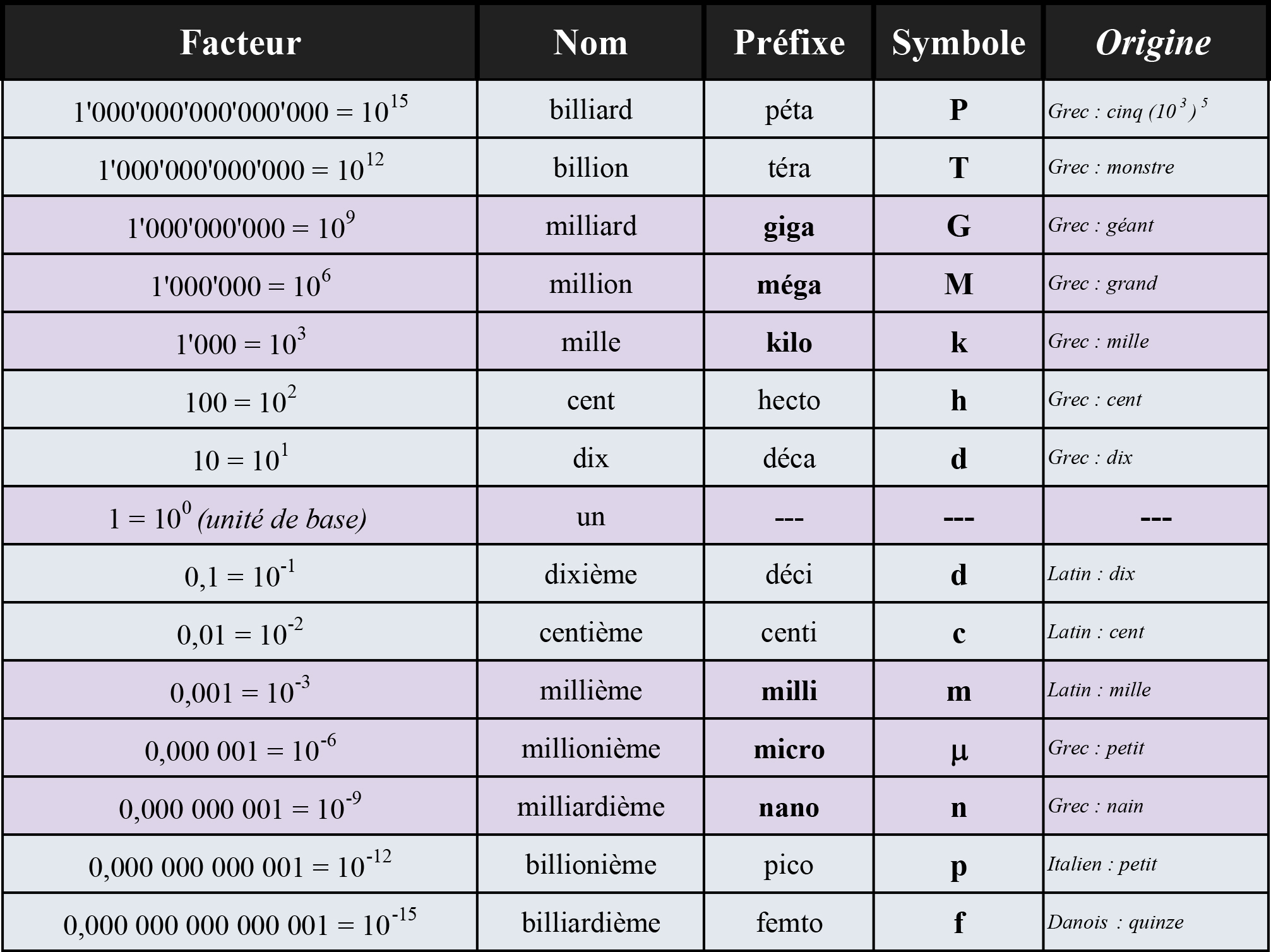
Fig. 1.1 Les préfixes et leur puissance de \(10\) pour les sous-unités. Les préfixes en gras sont à connaître pour ce cours.#
Astuce
Rappelez-vous que chaque préfixe correspond à une puissance de \(10\). Vous pouvez donc remplacer le préfixe par sa puissance de \(10\), et inversement, si besoin.
Par exemple :
Pour le préfixe \(kilo\) : \(k =\times 10^{3}\), donc :
\[8.2\,km=8.2\,(k)m=8.2\,(\times 10^{3})m=8.2\cdot 10^{3}\,m\]Pour le préfixe \(micro\) : \(\mu =\times 10^{-6}\), donc :
\[25.3\,\mu m=25.3\,(\mu )m=25.3(\times 10^{-6})m=25.3\cdot 10^{-6}\,m$$\]
Exemples d’écritures
Avec des puissances de \(10\) :
\(0.032\, m = 0.32\cdot 10^{-1}\, m = 3.2\cdot 10^{-2}\, m = 32\cdot 10^{-3}\, m\)
Avec les sous-unités :
\(0.032\, m = 0.32\, dm = 3.2\, cm = 32\, mm\)Avec des puissances de \(10\) :
\(3'000'000’000\, W = 3'000'000\cdot 10^{3}\, W = 3’000\cdot 10^{6}\, W = 3\cdot 10^{9}\, W\)
Avec les sous-unités :
\(3'000'000’000\, W = 3'000'000\, kW = 3’000\, MW = 3\, GW\)Avec des puissances de \(10\) :
\(0.000 000 002\, g = 0.000 002\cdot 10^{-3}\, g = 0.002\cdot 10^{-6}\, g = 2\cdot 10^{-9}g\)
Avec les sous-unités :
\(0.000 000 002\, g = 0.000 002\, mg = 0.002\, \mu g = 2\, ng\)
Conversion d’unités#
Il est souvent nécessaire de passer d’un type d’unité à un autre. Par exemple, si vous lisez un livre de cuisine, certaines quantités peuvent être exprimées en nombre de tasses et vous devez les convertir en litres. Ou peut-être lisez-vous, sur une carte américaine, les itinéraires d’un endroit à un autre et vous êtes intéressé par le nombre de kilomètres que vous parcourrez. Dans ce cas, vous devrez convertir des unités de miles en kilomètre.
Prenons un exemple simple de conversion d’unités. Disons que nous voulons convertir \(80\) mètres (\(m\)) en kilomètres (\(km\)).
La première chose à faire est de lister les unités dont vous disposez et les unités vers lesquelles vous souhaitez effectuer la conversion. Dans ce cas, nous avons des unités en mètres et nous voulons convertir en kilomètres.
Ensuite, nous devons déterminer un facteur de conversion reliant les mètres aux kilomètres. Un facteur de conversion est un rapport exprimant combien d’une unité est égale à une autre unité. Par exemple, il y a \(100\) centimètres dans \(1\) mètre, \(60\) secondes dans \(1\) minute, et ainsi de suite. Dans ce cas, on sait qu’il y a \(1'000\) mètres dans \(1\) kilomètre.
Nous pouvons maintenant configurer notre conversion d’unité. Nous écrirons les unités que nous avons, puis les multiplierons par le facteur de conversion afin que les unités s’annulent, comme indiqué:
Notez que l’unité \(m\) indésirable s’annule, ne laissant que l’unité \(km\) souhaitée. Vous pouvez utiliser cette méthode pour convertir entre n’importe quel type d’unité.
Dans le cas ou nous devons convertir une unité dans une sous-unité, il peut être plus facile d’utiliser les préfixes et les puissances de \(10\). Dans l’exemple précèdent nous voulons obtenir des kilomètres. Comme le préfixe kilo correspond à \(\cdot 10^{3}\), il faut faire apparaître cette puissance dans la réponse. Nous allons également nous aider d’une propriété des puissances de \(10\) qui dit que \(10^{n}\cdot 10^{-n}=10^{n-n}=10^{0}=1\).
Ce qui nous donne :
Exemples
Transformer : \(250\cdot 10^{8}\,\mu m\) en \(km\) (\(\mu=\) micro correspond à \(\cdot 10^{-6}\)) :
On transforme d’abord le préfixe \(\mu\) de la donnée en puissance de 10 :
\[250\cdot 10^{8}\,\mu m=250\cdot 10^{8}\cdot 10^{-6}\,m=250\cdot 10^{2}\,m\]Puis on fait apparaître le préfixe \(kilo =k =\cdot 10^{3}\) recherché :
\[\begin{split}\begin{align*} 250\cdot 10^{2}\,m &=250\cdot 10^{2}\cdot 10^{-3}\cdot 10^{3}\,m\\ &=250\cdot 10^{2}\cdot 10^{-3}\,km\\ &=250\cdot 10^{-1}\,km\\ &=25\,km \end{align*}\end{split}\]Transformer : \(5\cdot 10^{-1}\,km\) en \(nm\) (\(n=\) nano correspond à \(\cdot 10^{-9}\))
Transformer les \(km/h\) en \(m/s\)
Pour passer d’une vitesse exprimée en \(km/h\) vers les \(m/s\) (ou inversement) :
Pour passer des \(km/h\) aux \(m/s\), on divise par \(3.6\) \(\rightarrow\) \(72\,km/h ÷ 3.6 = 20\,m/s\)
Pour passer des \(m/s\) aux \(km/h\), on multiplie par \(3.6\) \(\rightarrow\) \(15\,m/s × 3.6 = 54\,km/h\)
Astuce :
Apprenez le facteur \(3.6\) et retenez que les kilomètres et les heures sont plus grand que les mètres et les secondes. On multiplie pour passer à quelque chose de plus grand (et inversement, on divise pour passer à quelque chose de plus petit).
Transformer les heures en minutes et secondes
Rappel :
La conversion des \(heures\) (\(h\)) en \(minutes\) (\(min\)) et \(secondes\) (\(s\)) est un peu différente, puisque :
YouTube
Quelques liens de vidéo utiles sur le même sujet :
Grandeurs, unités et symboles
Les grandeurs physique
