6.6. Exercices#
Exercice 1
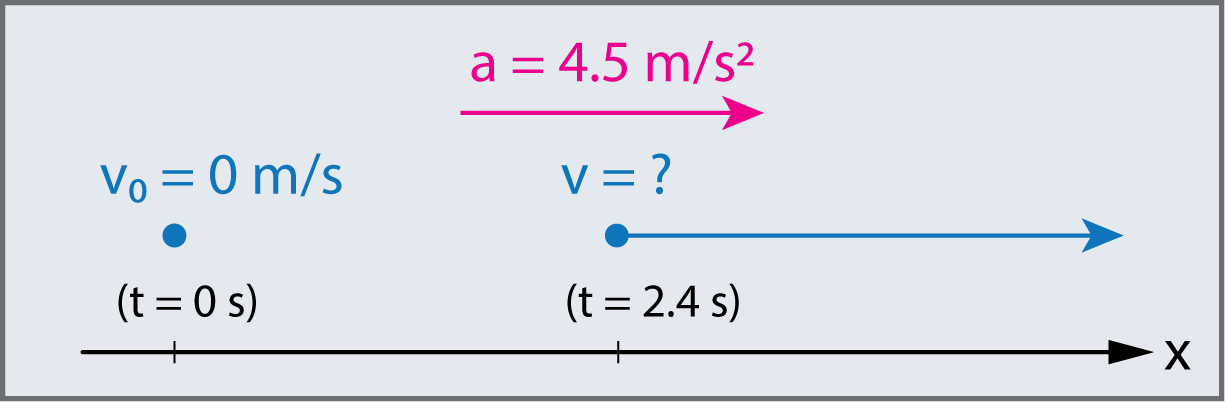
Un sprinter de classe olympique démarre une course avec une accélération de (\(4.50\,m/s^{2}\))
Quelle est sa vitesse \(2.40\,s\) plus tard ?
Tracez un graphique de sa position en fonction du temps pour cette période.
Exercice 2
Une balle bien lancée est attrapée dans un gant bien rembourré. Si la décélération de la balle est de \(a=2\cdot 10^{4}\,m/s^{2}\), et que \(1.85\,ms\) (\(1\,ms=1\cdot 10^{-3}\,s\)) s’écoule entre le moment où la balle touche le gant pour la première fois jusqu’à ce qu’elle s’arrête, quelle était la vitesse initiale de la balle ?
Exercice 3
Une balle dans une arme à feu est accélérée de la chambre de tir à l’extrémité du canon à un taux moyen de \(6.20\cdot 10^{5}\,m/s^{2}\) pour \(8.10\cdot 10^{-4}\,s\). Quelle est sa vitesse à la sortie du canon (c’est-à-dire sa vitesse finale) ?
Exercice 4
Un train régional accélère à une vitesse de \(1.35\,m/s^{2}\). Combien de temps faut-il pour atteindre sa vitesse maximale de \(80.0\,km/h\), en partant du repos ?
Le même train décélère habituellement à une vitesse de \(1.65\,m/s^{2}\). Combien de temps faut-il pour s’arrêter de sa vitesse maximale ?
En cas d’urgence, le train peut décélérer plus rapidement et s’arrêter de \(80.0\,km/h\) en \(8.30\,s\). Quelle est sa décélération d’urgence en \(m/s^{2}\) ?
Exercice 5
En entrant dans une autoroute, une voiture accélère depuis le repos à un taux de \(2.40\,m/s^{2}\) pendant \(12.0\,s\).
Faites un croquis de la situation.
Énumérez les éléments connus de ce problème.
Quelle est la distance parcourue par la voiture dans ces \(12.0\,s\) ? Pour résoudre cette partie, identifiez d’abord l’inconnu, puis expliquez comment vous avez choisi l’équation appropriée à résoudre. Après avoir choisi l’équation, montrez vos étapes de résolution de l’inconnu, vérifiez vos unités et discutez si la réponse est raisonnable.
Quelle est la vitesse finale de la voiture ? Résolvez cette inconnue de la même manière que dans la partie 3., en montrant toutes les étapes explicitement.
Exercice 6
À la fin d’une course de vélo, un coureur décélère à partir d’une vitesse de \(9.00\,m/s\) à un taux de \(2.00\,m/s^{2}\).
Quelle distance parcourra-t-il dans les 5 prochaines \(s\) ?
Quelle est sa vitesse à ce moment là ?
Évaluez le résultat. Est-ce que ça fait du sens ?
Exercice 7
(Application réelle) Le sang est accéléré du repos à \(30.0,cm/s\) sur une distance de \(1.80,cm\) par le ventricule gauche du cœur.
Faites un croquis de la situation.
Énumérez les éléments connus de ce problème.
Combien de temps dure l’accélération ? Pour résoudre cette partie, identifiez d’abord l’inconnu, puis expliquez comment vous avez choisi l’équation appropriée à résoudre. Après avoir choisi l’équation, montrez vos étapes de résolution de l’inconnu, en vérifiant vos unités.
La réponse est-elle raisonnable par rapport à la durée d’un battement de cœur ? newpage
solution
1.:::{figure} figures/ExercicesAcceleration7.jpg :name: Fig:ExercicesAcceleration7 :align: center :width: 50%
2. On connait: $v_{0}=0\,m/s$, $v=30,cm/s=0.30\,m/s$ et $Delta x=1.80,cm=1.8\cdot 10^{-2}\,m$
3. On cherche $t$. On utilise l'équation qui contient les valeurs connues en 2. et l'inconnue; on utilise $\vec{Delta x}=\dfrac{\vec{v}+\vec{v_{0}}}{2}\cdot t$, ce qui donne:
begin{align*}
\vec{Delta x} &=\dfrac{\vec{v}+\vec{v_{0}}}{2}\cdot t
\\Rightarrowquad t &=\dfrac{\vec{Delta x}}{\left(\dfrac{\vec{v}+\vec{v_{0}}}{2}\right)}
t &=\dfrac{2\vec{Delta x}}{\vec{v}+\vec{v_{0}}}
t &=\dfrac{2\cdot 1.8\cdot 10^{-2},m}{(0.30\,m/s+0.0\,m/s)}
t &=0.12,s
end{align*}
L'ordre de grandeur de la réponse semble raisonnable. En moyenne, l'être humain est à 60 pulsations par minute, soit une pulsation par seconde. Chaque pulsation se compose de 4 phases (remplissage/vidage des ventricules gauche et droite), donc $0.12\,s$ semble raisonnable.
Exercice 8
Lors d’un tir, un joueur de hockey accélère la rondelle d’une vitesse de \(8.00\,m/s\) à \(40.0\,m/s\) dans la même direction. Si ce coup prend \(3.33\cdot 10^{-2}\,s\), calculez la distance sur laquelle la rondelle accélère.
Exercice 9
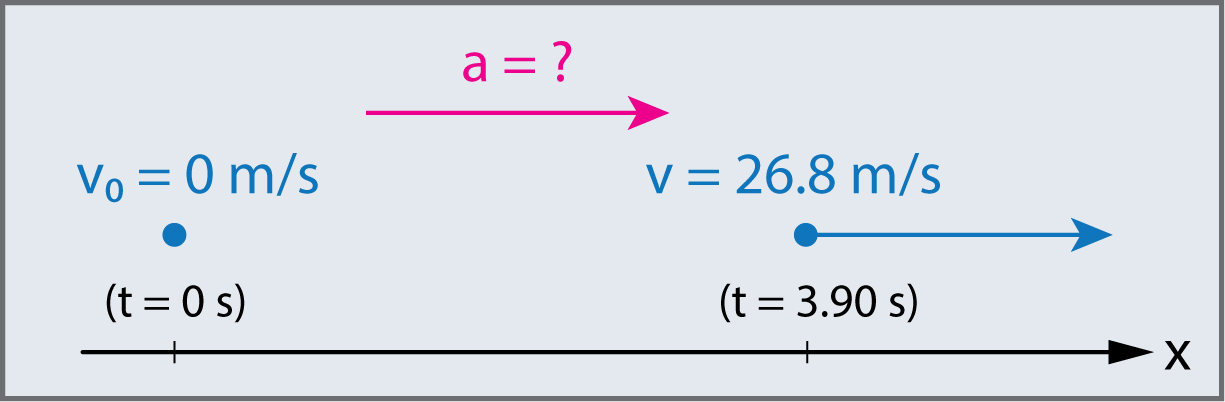
Une moto puissante peut accélérer du repos à \(26.8\,m/s\) (\(100\,km/h\)) en seulement \(3.90\,s\).
Quelle est son accélération moyenne ?
Quelle est la distance parcourue pendant cette période ?
solution
\(\vec{a}=\dfrac{\vec{\Delta v}}{t}=\dfrac{26.8\,m/s}{3.90,s}=6.8718\,m/s^{2}=6.87\,m/s^{2}\)
\(\vec{\Delta x}=\dfrac{\vec{v}+\vec{v_{0}}}{2}\cdot t=\dfrac{26.8\,m/s+0\,m/s}{2}\cdot 3.90,s=52.3\,m\)
On obtient le même résultat avec \(\vec{\Delta x}=\dfrac{1}{2}\vec{a}t^{2}+\vec{v_{0}}t=\dfrac{1}{2}\cdot (6.8718\,m/s^{2})\cdot (3.90\,m/s)^{2}=52.3\,m\)
(on fera attention à ne pas prendre une valeur arrondie pour \(a\))
Exercice 10
Les trains de marchandises ne peuvent produire que des accélérations et des décélérations relativement faibles.
Quelle est la vitesse finale d’un train de marchandises qui accélère à un taux de \(0.0500\,m/s^{2}\) pendant \(8.00\,min\), en commençant par une vitesse initiale de \(4.00\,m/s\) ?
Si le train peut ralentir avec un taux de \(0.550\,m/s^{2}\), combien de temps faudra-t-il pour s’arrêter à cette vitesse ?
Quelle distance parcourra-t-il dans chaque cas ?
Exercice 11
Un obus de feu d’artifice est accéléré du repos à une vitesse de \(65\,m/s\) sur une distance de \(0.250\,m\).
Combien de temps l’accélération a-t-elle durée ?
Calculez l’accélération.
solution
\(\vec{Delta x}=\dfrac{\vec{v}+\vec{v_{0}}}{2}\cdot t\) Donc \(t=\dfrac{2\vec{Delta x}}{\vec{v}+\vec{v_{0}}}=\dfrac{2\cdot 0.250,m}{65\,m/s+0\,m/s}=0.0076923,s=7.69,ms\)
\(\vec{a}=\dfrac{\vec{Delta v}}{t}=\dfrac{65\,m/s}{0.0076923,s}=8'450\,m/s^{2}\) ou bien \(\vec{v}^2-\vec{v_{0}}^{2}=2\vec{a}\vec{Delta x}\) \(\Rightarrow\) \(\vec{a}=\dfrac{\vec{v}^2-\vec{v_{0}}^{2}}{2\vec{Delta x}}=\dfrac{(65\,m/s)^2}{2\cdot 0.250,m}=8'450\,m/s^{2}\)
Exercice 12
Un cygne sur un lac s’envole en battant des ailes et en courant au-dessus de l’eau.
Si le cygne doit atteindre une vitesse de \(6.00\,m/s\) pour décoller et qu’il accélère depuis le repos à un taux moyen de \(0.350\,m/s^{2}\), quelle distance parcourra-t-il avant de prendre le vol ?
Combien de temps cela prend-il ?
solution
\(\vec{v}^2-\vec{v_{0}}^{2}=2\vec{a}\vec{Delta x}\) \(\Rightarrow\) \(\vec{Delta x}=\dfrac{\vec{v}^2-\vec{v_{0}}^{2}}{2\vec{a}}=\dfrac{(6.00\,m/s)^2-(0\,m/s)^{2}}{2\cdot 0.350\,m/s^{2}}=51.4\,m\)
\(t=\dfrac{\vec{Delta v}}{\vec{a}}=\dfrac{6.00\,m/s}{0.350\,m/s^{2}}=17.1\,s\)
Exercice 13
(Application réelle) Le cerveau d’un Pic vert est spécialement protégé contre les grandes décélérations par des attaches en forme de tendon à l’intérieur du crâne. En picorant sur un arbre, la tête du pic s’arrête depuis une vitesse initiale de \(25.0\,km/h\) sur une distance de seulement \(2.00\,mm\).
Trouvez l’accélération en \(m/s^{2}\) et en multiples de \(g\) (\(g=9.81\,m/s^{2}\)).
Calculez le temps d’arrêt.
Les tendons berçant le cerveau s’étirent, ce qui rend sa distance d’arrêt de \(4.50,mm\) (plus grande que la tête et, par conséquent, moins de décélération du cerveau). Quelle est la décélération du cerveau, exprimée en multiples de \(g\) ?
solution
Premièrement: \(25\,km/h\div 3.6=6.94\,m/s\) et on utilise \(\vec{v}^2-\vec{v_{0}}^{2}=2\vec{a}\vec{Delta x}\) \(\Rightarrow\) \(\vec{a}=\dfrac{\vec{v}^2-\vec{v_{0}}^{2}}{2\vec{Delta x}}=\dfrac{(0\,m/s)^{2}-(6.94\,m/s)^2}{2\cdot 2.00\cdot 10^{-3},m}=\dfrac{-48.16}{4}\cdot 10^{3}\,m/s^{2}=-12'040\,m/s^{2}=-1'230\cdot g\) Le Pic vert est l’être vivant qui peut supporter la plus grand décélération.
\(\vec{Delta x}=\dfrac{\vec{v}+\vec{v_{0}}}{2}\cdot t\) \(\Rightarrow\) \(t=\dfrac{2\vec{Delta x}}{\vec{v}+\vec{v_{0}}}=\dfrac{2\cdot 2.00\cdot 10^{-3},m}{0\,m/s+6.94\,m/s}=0.000576,s=576,mu s\)
\(\vec{a}=\dfrac{\vec{v}^2-\vec{v_{0}}^{2}}{2\vec{Delta x}}=\dfrac{(0\,m/s)^{2}-(6.94\,m/s)^2}{2\cdot 4.5\cdot 10^{-3},m}=\dfrac{-48.16}{9}\cdot 10^{3}\,m/s^{2}=-5'352\,m/s^{2}=-546\cdot g\)
Exercice 14
Un footballeur imprudent entre en collision avec un poteau de but rembourré alors qu’il court à une vitesse de \(7.50\,m/s\) et s’arrête complètement après avoir comprimé le rembourrage et son corps à \(0.350\,m\).
Quelle est sa décélération ?
Combien de temps dure la collision ?
solution
\(\vec{v}^2-\vec{v_{0}}^{2}=2\vec{a}\vec{Delta x}\) \(\Rightarrow\) \(\vec{a}=\dfrac{\vec{v}^2-\vec{v_{0}}^{2}}{2\vec{Delta x}}=\dfrac{(0\,m/s)^{2}-(7.50\,m/s)^2}{2\cdot 0.350,m}=\dfrac{-56.25}{0.7}\,m/s^{2}=-80.357\,m/s^{2}=-80.4\,m/s^{2}\)
\(t=\dfrac{\vec{Delta v}}{\vec{a}}=\dfrac{-7.50\,m/s}{-80.357\,m/s^{2}}=0.0933,s=93.3,ms\)
Exercice 15
Au cours de la Seconde Guerre mondiale, il y a eu plusieurs cas signalés d’aviateurs qui ont sauté de leurs avions en flammes sans parachute pour échapper à une mort certaine. Certains sont tombés à environ \(6'000\) mètres, et certains d’entre eux ont survécu, avec quelques blessures potentiellement mortelles. Pour ces pilotes chanceux, les branches d’arbres et les tas de neige au sol ont permis à leur décélération d’être relativement faible. Si nous supposons que la vitesse d’un pilote lors de l’impact était de \(54\,m/s\), quelle a été sa décélération ? Supposons que les arbres et la neige l’ont arrêté sur une distance de \(3.0\,m\).
solution
\(\vec{a}=\dfrac{\vec{v}^2-\vec{v_{0}}^{2}}{2\vec{Delta x}}=\dfrac{(0\,m/s)^{2}-(54\,m/s)^2}{2\cdot 3.0,m}=\dfrac{-2916}{6}\,m/s^{2}=-486\,m/s^{2}\)
Exercice 16
Prenons l’exemple d’un écureuil tombant d’un arbre au sol.
Si nous ignorons la résistance de l’air dans ce cas (uniquement pour le bien de ce problème), déterminez la vitesse d’un écureuil juste avant de toucher le sol, en supposant qu’il est tombé d’une hauteur de \(3.0\,m\).
Si l’écureuil s’arrête SUR une distance de \(2.0\,cm\) en pliant ses pattes, comparez sa décélération avec celle de l’aviateur dans le problème précédent.
solution
\(\vec{a}=\vec{g}=9.81\,m/s^{2}\) \(\vec{v}^2-\vec{v_{0}}^{2}=2\vec{g}\vec{Delta x}\) \(\Rightarrow\) \(v=\sqrt{2\vec{g}\vec{Delta x}-\vec{v_{0}}^{2}}=\sqrt{2\cdot 9.81\,m/s^{2}\cdot 3.0,m-(0\,m/s)^{2}}=\sqrt{58.86}=7.7\,m/s=28\,km/h\)
\(\vec{a}=\dfrac{\vec{v}^2-\vec{v_{0}}^{2}}{2\vec{Delta x}}=\dfrac{(0\,m/s)^{2}-(7.7\,m/s)^2}{2\cdot 2.0\cdot 10^{-2},m}=\dfrac{-58.86}{4.0\cdot 10^{-2}}\,m/s^{2}=-1471.5\,m/s^{2}=-1'470\,m/s^{2}\) La décélération de l’écureuil est 3 fois plus importante que celle de l’aviateur (!)
Exercice 17
Un train express passe par une gare. Il entre avec une vitesse initiale de \(22.0\,m/s\) et décélère avec à un taux de \(0.150\,m/s^{2}\) quand il passe. Le quai de la gare mesure \(210\,m\) de long.
Combien de temps le bout du nez de la locomotive du train expresse passe-t-il dans la gare ?
Quelle est la vitesse du train lorsque le nez quitte la gare ?
Si le train mesure \(130\,m\) de long, quand est-ce que l’extrémité du train quitte la gare ?
Quelle est la vitesse de l’extrémité du train à sa sortie ?
solution
\(\vec{Delta x}=frac{1}{2}\vec{a}t^{2}+\vec{v_{0}}t=frac{1}{2}(-0.150\,m/s^{2})\cdot (t)^{2}+(22.0\,m/s)\cdot t=210\,m\) \(\Rightarrow\) \(-0.075\cdot t^{2}+22\cdot t-210=0\), qui a pour solutions: \(t=\dfrac{-22\Rightarrow\sqrt{22^2-[4\cdot (-0.075)\cdot (-210)]}}{-2\cdot 0.075}=\dfrac{-22\Rightarrow\sqrt{421}}{-0.15}=\dfrac{-22\Rightarrow 20.5}{-0.15}\) \(\Rightarrow\) \(t_{1}=10.0\,s\) et \(t_{2}=283\,s\). Le bout du nez du train met \(10.0\,s\) pour traverser la gare.
\(\vec{v}=\vec{a}t+\vec{v_{0}}=(-0.15\,m/s^{2}\cdot 10.0,s+22.0\,m/s=20.5\,m/s\)
Quand le bout du nez du train entre en gare, l’extrémité du train se trouve à une distance de \(210,m+130,m=330\,m\) de la fin du quai. Selon 1., on va obtenir: \(-0.075\cdot t^{2}+22\cdot t-330=0\) qui a pour solution: \(t_{1}=15.9\,s\) et \(t_{2}=277\,s\). L’extrémité du train sort de la gare \(15.9\,s\) après l’entrée du train en gare.
à \(t=15.9\,s\) le train a une vitesse de \(\vec{v}=\vec{a}t+\vec{v_{0}}=-0.15\,m/s^{2}\cdot 15.9,s+22.0\,m/s=19.6\,m/s\)
Exercice 18
Les dragsters peuvent atteindre une vitesse de pointe de \(145\,m/s\) en seulement \(4.45\,s\).
Calculez l’accélération moyenne pour un dragster.
Trouvez la vitesse finale d’un dragster en partant du repos et en accélérant avec la taux trouvé en 1. sur \(402\,m\) (un quart de mille) sans utiliser aucune information sur le temps.
Pourquoi la vitesse finale est-elle supérieure à celle utilisée pour trouver l’accélération moyenne ? Astuce: vérifiez si l’hypothèse d’une accélération constante est valide pour un dragster. Sinon, discutez si l’accélération serait plus grande au début ou à la fin de la course et quel effet cela aurait sur la vitesse finale.
solution
\(\vec{a}=\dfrac{\vec{Delta v}}{t}=\dfrac{145\,m/s}{4.45,s}=32.9\,m/s^{2}\)
\(\vec{v}^2-\vec{v_{0}}^{2}=2\vec{a}\vec{Delta x}\) \(\Rightarrow\) \(v=\sqrt{2\vec{a}\vec{Delta x}-\vec{v_{0}}^{2}}=\sqrt{2\cdot 32.9\,m/s^{2}\cdot 402,m-(0\,m/s)^{2}}=\sqrt{26'452}=163\,m/s=586\,km/h\)
\(145\,m/s\) en seulement \(4.45\,s\) correspond à une distance de \(322.6\,m\). L’accélération du dragster n’est certainement pas constante. L’accélération diminue; plus il va vite, moins il arrive à accélérer. En faisant l’hypothèse d’une accélération constante, on trouve forcement une vitesse plus grande que dans la réalité.
Exercice 19
Un coureur de vélo sprinte à la fin d’une course pour décrocher une victoire. Le coureur a une vitesse initiale de \(11.5\,m/s\) et accélère avec un taux de \(0.500\,m/s^{2}\) pendant \(7.00\,s\).
Quelle est sa vitesse finale ?
Le coureur continue à cette vitesse jusqu’à la ligne d’arrivée. S’il était à \(300\,m\) de la ligne d’arrivée lorsqu’il a commencé à accélérer, combien de temps a-t-il gagné ?
Un autre coureur avait \(5.00\,m\) d’avance lorsque le vainqueur a commencé à accélérer, mais il n’a pas pu accélérer et a roulé à \(11.8\,m/s\) jusqu’à la ligne d’arrivée. À quelle distance (en mètres et en secondes) de lui le vainqueur a-t-il terminé ?
solution
\(\vec{v}=\vec{a}t+\vec{v_{0}}=0.500\,m/s^{2}\cdot 7.00,s+11.5\,m/s=15.0\,m/s\)
Sans accélération: \(t=\dfrac{\vec{Delta x}}{\vec{v_{moy}}}=\dfrac{300,m}{11.5\,m/s}=26.1\,s\) Avec accélération: \(Delta \vec{x_{acc}}=frac{1}{2}\vec{a}\cdot t^{2}+\vec{v_{0}}\cdot t=frac{1}{2}\cdot (0.500\,m/s^{2})\cdot (7.00,s)^{2}+11.5\,m/s\cdot 7.00,s=92.75\,m\) Il lui reste donc \(300,m-92.75,m=207.25\,m\) à faire à la vitesse de \(15.0\,m/s\), c’est à dire: \(t_{15\,m/s}=\dfrac{\vec{Delta x}}{\vec{v_{moy}}}=\dfrac{207.25,m}{15.0\,m/s}=13.8\,s\) Il a donc gagné \(26.1,s-(7.00,s+13.8,s)=26.1,s-20.8,s=5.30\,s\)
\(t_{2^{e},coureur}=\dfrac{\vec{Delta x}}{\vec{v_{moy}}}=\dfrac{300,m-5.00,m}{11.8\,m/s}=25.0\,s\) Le vainqueur finit donc \(25.0-20.8=4.20\,s\) devant le 2\(^{e}\) \(4.20\,s\) à la vitesse de \(11.8\,m/s\) correspond à une distance de \(\vec{Delta x}=\vec{v_{moy}}\cdot t=11.8\,m/s\cdot 4.20,s=49.6\,m\)
Exercice 20
En 1967, le Néo-Zélandais Burt Munro a établi le record du monde d’un moto, sur le désert de sel des Salt Flats de Bonneville dans l’Utah, avec une vitesse maximale de \(295.45\,km/h\). Le parcours à sens unique était de \(8.00,km\) de long. Les accélérations sont souvent décrits par le temps nécessaire pour atteindre \(100\,km/h\) depuis le départ. Si ce temps était de \(4.00\,s\) et que Burt accélérait à ce rythme jusqu’à ce qu’il atteigne sa vitesse maximale, combien de temps a-t-il fallu à Burt pour terminer le parcours ?
solution
\(\vec{v_{max}}=295.45\,km/h\div 3.6=82.069\,m/s\), \(\vec{v_{0}}=0\,m/s\) et \(\vec{a}=frac{100\,km/h}{4.00,s}=frac{27.78\,m/s}{4.00,s}=6.94\,m/s^{2}\) \(\vec{v_{max}}=\vec{a}\cdot t_{v_{max}}+\vec{v_{0}}\) \(\Rightarrow\) \(t_{v_{max}}=\dfrac{\vec{v_{max}}}{\vec{a}}=\dfrac{82.069\,m/s}{6.94\,m/s^{2}}=11.82\,s\) pour atteindre \(v_{max}\). Pendant ce temps, il a parcourut une distance de \(\vec{Delta x}=frac{1}{2}\vec{a}t^{2}=frac{1}{2}(6.94\,m/s^{2})\cdot (11.82)^{2}=484.8\,m\) Il lui reste donc \(8'000,m-484.4,m=7'515.2\,m\) à parcourir à la vitesse constante de \(82.069\,m/s\), qu’il fait en \(t=\dfrac{\vec{Delta x}}{\vec{v_{moy}}}=\dfrac{7'515.2,m}{82.069\,m/s}=91.57\,s\). Le temps total du parcourt est donc de \(11.82,s+91.57,s=103.4,s=1,min, 43.4\,s\)
Exercice 21
Un record du monde a été établi pour le \(100\,m\) masculin aux Jeux olympiques de 2008 à Beijing par Usain Bolt de la Jamaïque. Bolt a franchi la ligne d’arrivée avec un temps de \(9.69\,s\). Si nous supposons que Bolt a accéléré pendant \(3.00\,s\) pour atteindre sa vitesse maximale, et a maintenu cette vitesse pour le reste de la course, calculez sa vitesse maximale et son accélération.
Au cours des mêmes Jeux Olympiques, Bolt a également établi le record du monde du \(200\,m\) avec un temps de \(19.30\,s\). En utilisant les mêmes hypothèses que pour le \(100\,m\), quelle était sa vitesse maximale pour cette course ?
solution
1.begin{center} includegraphics[scale=0.5]{CI-ExercicesAccelerationBolt.jpg} %—- ou .pdf .png end{center} On écrit: \(\vec{Delta x_{1}}=x_{1}-x_{0}\) et \(\vec{Delta x_{2}}=x_{2}-x_{1}\), avec \(\vec{Delta x_{1}}+\vec{Delta x_{2}}=100\,m\) 1\(^{ère}\) Partie: \(\vec{v_{max}}=\vec{a}t_{1}+\vec{v_{0}}=3\vec{a}\) \(\Rightarrow\) \(\vec{a}=frac{\vec{v_{max}}}{3}\) et \(\vec{Delta x_{1}}=\dfrac{\vec{v_{max}}+\vec{v_{0}}}{2}t=\dfrac{3}{2}\vec{v_{max}}=1.5\cdot\vec{v_{max}}\) 2\(^{e}\) Partie: \(\vec{Delta x_{2}}=\vec{v_{max}}\cdot Delta t_{2}=\vec{v_{max}}\cdot (t_{2}-t_{1})=6.69\cdot\vec{v_{max}}\) Au total: \(\vec{Delta x_{1}}+\vec{Delta x_{2}}=1.5\cdot\vec{v_{max}}+6.69\cdot\vec{v_{max}}=8.19\cdot\vec{v_{max}}=100\,m\) et donc: \(\vec{v_{max}}=\dfrac{100,m}{8.19,s}=12.2\,m/s=44.0\,km/h\) et \(\vec{a}=\dfrac{\vec{v_{max}}}{3}=4.07\,m/s^{2}\) 2. Comme on a la même accélération pendant le même temps, on peut directement écrire: \(\vec{Delta x_{1}}+\vec{Delta x_{2}}=200\,m\) \(\vec{a}=\dfrac{\vec{v_{max}}}{3}\) \(\vec{Delta x_{1}}=1.5\cdot\vec{v_{max}}\) \(\vec{Delta x_{2}}=\vec{v_{max}}\cdot (19.30,s-3.00,s)=16.30\cdot\vec{v_{max}}\) Ce qui nous donne: \(\vec{Delta x_{1}}+\vec{Delta x_{2}}=1.5\cdot\vec{v_{max}}+16.30\cdot\vec{v_{max}}=17.80\cdot\vec{v_{max}}=200\,m\) et donc \(\vec{v_{max}}=\dfrac{200,m}{17.80,s}=11.2\,m/s=40.4\,km/h\)