9.3. La 2^ème loi de Newton

Le concept de système physique

La deuxième loi du mouvement de Newton est étroitement liée à la première loi du mouvement de Newton. Il énonce mathématiquement la relation de cause à effet entre la force et les changements de mouvement. La deuxième loi du mouvement de Newton est plus quantitative et est largement utilisée pour calculer ce qui se passe dans des situations impliquant une force. Avant de pouvoir écrire la deuxième loi de Newton sous la forme d’une simple équation donnant la relation exacte entre la force, la masse et l’accélération, nous devons affiner certaines idées qui ont déjà été mentionnées.

Premièrement, qu’entend-on par changement de mouvement? La réponse est qu’un changement de mouvement équivaut à un changement de vitesse. Un changement de vitesse signifie, par définition, qu’il y a une accélération. La première loi de Newton dit qu’une force externe résultante provoque un changement de mouvement; ainsi, nous voyons qu’une force externe résultante provoque une accélération.

Une autre question se pose immédiatement. Qu’entend-on par force extérieure? Une notion intuitive d’externe est correcte - une force extérieur agit de l’extérieur du système physique d’intérêt. Par exemple, dans la Fig. 9.4(a), le système physique d’intérêt est le wagon plus l’enfant qui s’y trouve. Les deux forces exercées par les autres enfants sont des forces extérieures. Une force interne agit entre les éléments du système. En regardant à nouveau la Fig. 9.4(a), la force exercée par l’enfant dans le wagon pour s’accrocher au wagon est une force interne entre les éléments du système d’intérêt. Seules les forces externes affectent le mouvement d’un système, selon la première loi de Newton. (Les forces internes s’annulent en fait, comme nous le verrons dans la section suivante). Vous devez définir les limites du système avant de pouvoir déterminer les forces externes. Parfois, le système est évident, tandis que d’autres fois, l’identification des limites d’un système est plus subtile. Le concept de système est fondamental dans de nombreux domaines de la physique, tout comme l’application correcte des lois de Newton. Ce concept sera revisité à plusieurs reprises au cours de notre voyage à travers la physique.

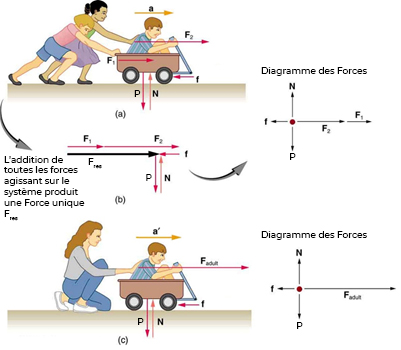
Fig. 9.4 Différentes forces exercées sur la même masse produisent des accélérations différentes. (a) Deux enfants poussent un chariot avec un enfant à l’intérieur. Les flèches représentant toutes les forces externes sont affichées. Le système d’intérêt est le wagon et son conducteur. Le poids \(\vec{P}\) du système et du support du sol \(\vec{N}\) sont également indiqués pour être complets et sont supposés être annulés. Le vecteur \(\vec{f}\) représente le frottement agissant sur le wagon, et il agit vers la gauche, s’opposant au mouvement du wagon. (b) Toutes les forces externes agissant sur le système s’additionnent pour produire une force résultante, \(\vec{F}_{res}\). Le diagramme des forces montre toutes les forces agissant sur le système d’intérêt. Le point représente le centre de masse du système. Chaque vecteur de force s’étend de ce point. Parce qu’il y a deux forces agissant vers la droite, nous dessinons les vecteurs de manière colinéaire. (c) Une force externe résultante plus importante produit une accélération plus importante (\(a'>a\)) lorsqu’un adulte pousse l’enfant. (crédit : openstax.org)

Or, il semble raisonnable que l’accélération soit directement proportionnelle et dans le même sens que la force externe résultante (totale) agissant sur un système. Cette hypothèse a été vérifiée expérimentalement et est illustrée à la Fig. 9.4. Dans la partie (a), une force plus petite provoque une accélération plus petite que la force plus grande illustrée dans la partie (c). Par souci d’exhaustivité, les forces verticales sont également indiquées; ils sont supposés s’annuler car il n’y a pas d’accélération dans le sens vertical. Les forces verticales sont le poids \(\vec{P}\) et le support du terrain \(\vec{N}\), et la force horizontale \(\vec{f}\) représente la force de friction. Ceux-ci seront discutés plus en détail dans les sections suivantes. Pour l’instant, nous définirons le frottement comme une force qui s’oppose au mouvement des objets qui se touchent. La Fig. 9.4(b) montre comment les vecteurs représentant les forces externes s’additionnent pour produire une force résultante, \(\vec{F}_{res}\) :

\[\Sigma\vec{F}=\vec{F}_{res}\]

Pour obtenir une équation pour la deuxième loi de Newton, nous écrivons d’abord la relation de l’accélération et de la force externe résultante comme la proportionnalité :

\[\vec{a}\propto\vec{F}_{res}\]

où le symbole \(\propto\) signifie proportionnel à, et \(\vec{F}_{res}\) est la force externe résultante. (La force externe résultante est la somme vectorielle de toutes les forces externes et peut être déterminée graphiquement, en utilisant la méthode tête-à-queue, ou analytiquement, en utilisant des composants. Les techniques sont les mêmes que pour l’addition d’autres vecteurs.) Cette proportionnalité énonce ce que nous avons dit en mots - l'accélération est directement proportionnelle à la force externe résultante. Une fois le système d’intérêt choisi, il est important d’identifier les forces externes et d’ignorer les forces internes. C’est une énorme simplification de ne pas avoir à prendre en compte les nombreuses forces internes agissant entre les objets du système, telles que les forces musculaires dans le corps de l’enfant, sans parler de la myriade de forces entre les atomes des objets, mais ce faisant, nous pouvons facilement résoudre certains problèmes très complexes avec seulement une erreur minime grâce à notre simplification.

Or, il semble également raisonnable que l’accélération soit inversement proportionnelle à la masse du système. En d’autres termes, plus la masse (l’inertie) est grande, plus l’accélération produite par une force donnée est petite. Et en effet, comme l’illustre la Fig. 9.5, la même force externe résultante appliquée à une voiture produit une accélération beaucoup plus faible que lorsqu’elle est appliquée à un ballon de basket. La proportionnalité s’écrit :

\[a\propto\dfrac{1}{m}\]

où \(m\) est la masse du système. Des expériences ont montré que l’accélération est exactement inversement proportionnelle à la masse, tout comme elle est exactement linéairement proportionnelle à la force externe résultante.

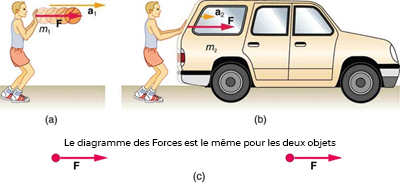
Fig. 9.5 La même force exercée sur des systèmes de masses différentes produit des accélérations différentes. (a) Un basketteur pousse un ballon de basket pour faire une passe. (L’effet de la gravité sur la balle est ignoré.) (b) Le même joueur exerce une force identique sur un SUV calé et produit une accélération beaucoup plus petite (même si le frottement est négligeable). (c) Les diagrammes des forces sont identiques, permettant une comparaison directe des deux situations. Une série de modèles pour le diagramme des forces émergera au fur et à mesure que vous poserez plus de problèmes. (crédit : openstax.org)

On a constaté que l’accélération d’un objet ne dépend que de la force externe résultante et de la masse de l’objet. La combinaison des deux proportionnalités qui viennent d’être données donne la deuxième loi du mouvement de Newton.

Deuxième Loi de Newton

L’accélération d’un système est directement proportionnelle et dans le même sens que la force externe résultante agissant sur le système, et inversement proportionnelle à sa masse.
Sous forme d’équation, la deuxième loi du mouvement de Newton est

\[\vec{a}=\dfrac{\Sigma\vec{F}}{m}=\dfrac{\vec{F}_{res}}{m}\]

Ceci est souvent écrit sous la forme la plus familière

\[\Sigma\vec{F}=\vec{F}_{res}=m\cdot\vec{a}\]

Lorsque seule l’amplitude de la force résultante et de l’accélération sont considérées, cette équation est simplement

\[F_{res}=m\cdot a\]

Bien que ces deux dernières équations soient vraiment les mêmes, la première donne plus d’informations sur ce que signifie la deuxième loi de Newton. La loi est une relation de cause à effet entre trois grandeurs qui n’est pas simplement basée sur leurs définitions. La validité de la deuxième loi repose entièrement sur la vérification expérimentale.

Unité de la force

\(F_{res}=m\cdot a\) est utilisé pour définir l’unité de force en termes de trois unités de base pour la masse, la longueur et le temps. L’unité de force SI s’appelle le Newton (abrégé \(N\)).
\(1.0\,N\) correspond à la force nécessaire pour accélérer un objet de \(1.0\,kg\) au taux de \(1.0\,m/s^{2}\). Autrement dit, puisque \(F_{res}=m\cdot a\)

\[1\,N=1\,kg\cdot 1\,m/s^{2}=\dfrac{kg\cdot m}{s^{2}}\]

Alors que presque le monde entier utilise le newton comme unité de force, aux États-Unis, l’unité de force la plus connue est la livre (\(lb\)), où \(1\,N=0.225\,lb\).

9.4. Poids et force gravitationnelle

Lorsqu’un objet tombe, il accélère vers le centre de la Terre. La deuxième loi de Newton stipule qu’une force résultante sur un objet est responsable de son accélération. Si la résistance de l’air est négligeable, la force résultante sur un objet qui tombe est la force gravitationnelle, communément appelée son poids \(\vec{P}\). Le poids peut être désigné comme un \(\vec{P}\) parce qu’il a une direction; vers le bas est, par définition, la direction de la gravité et, par conséquent, le poids est une force vers le bas. L’amplitude du poids est notée \(P\). Galilée a contribué à montrer qu’en l’absence de résistance de l’air, tous les objets tombent avec la même accélération \(\vec{g}\). En utilisant le résultat de Galilée et la deuxième loi de Newton, nous pouvons dériver une équation pour le poids.

Considérons un objet avec une masse \(m\) tomber vers le bas vers la Terre. Il ne subit que la force de gravité descendante, qui a une amplitude \(P\). La deuxième loi de Newton stipule que l’amplitude de la force externe résultante sur un objet est \(\vec{F}_{res}=m\cdot\vec{a}\).

Puisque l’objet ne subit que la force de gravité descendante, \(\vec{F}_{res}=\vec{P}\). Nous savons que l’accélération d’un objet due à la gravité est \(\vec{g}\), ou \(\vec{a}=\vec{g}\). En les substituant à la seconde loi de Newton, on obtient :

Le Poids

L’équation du poids \(\vec{P}\) - la force gravitationnelle sur une masse \(m\) - est donnée par :

\[\vec{P}=m\cdot \vec{g}\]

Puisque \(g=9.8\,m/s^{2}\) en moyenne sur Terre, le poids d’un objet de \(1,0\,kg\) sur Terre est de \(9.81\,N\), comme on le voit:

\[P=m\cdot g=1.0\,kg\cdot 9.81\,m/s^{2}=9.81\,N\]

Rappelons que \(\vec{g}\) peut prendre une valeur positive ou négative, selon la direction positive du système de coordonnées utilisé. Assurez-vous de prendre cela en considération lorsque vous résolvez des problèmes de poids.

Lorsque la force externe résultante sur un objet est son poids, on dit qu’il est en *chute libre. Autrement dit, la seule force agissant sur l’objet est la force de gravité. Dans le monde réel, lorsque des objets tombent vers le bas vers la Terre, ils ne sont jamais vraiment en chute libre car il y a toujours une force ascendante de l’air agissant sur l’objet.

L’accélération due à la gravité \(\vec{g}\) varie légèrement sur la surface de la Terre, de sorte que le poids d’un objet dépend de l’emplacement et n’est pas une propriété intrinsèque de l’objet. Le poids varie considérablement si l’on quitte la surface de la Terre. Sur la Lune, par exemple, l’accélération due à la gravité n’est que \(1.67\,m/s^{2}\). Une masse de \(1.0\,kg\) a donc un poids de \(9.8\,N\) sur Terre et seulement environ \(1.7\,N\) sur la Lune.

La définition la plus large du poids dans ce sens est que le poids d’un objet est la force gravitationnelle exercée sur lui par le grand corps le plus proche, comme la Terre, la Lune, le Soleil, etc. C’est la définition la plus courante et la plus utile du poids en physique. Cependant, elle diffère considérablement de la définition du poids utilisée par la NASA et les médias populaires en ce qui concerne les voyages et l’exploration spatiaux. Lorsqu’ils parlent d’apesanteur et de microgravité, ils se réfèrent en réalité au phénomène que nous appelons chute libre en physique. Nous utiliserons la définition ci-dessus du poids, et nous ferons une distinction minutieuse entre la chute libre et l’apesanteur réelle.

Il est important de savoir que le poids et la masse sont des quantités physiques très différentes, bien qu’elles soient étroitement liées. La masse est la quantité de matière et ne varie pas en physique classique, alors que le poids est la force gravitationnelle et varie en fonction de la gravité, de la planète. Il est tentant d’assimiler les deux, car la plupart de nos exemples se déroulent sur Terre, où le poids d’un objet ne varie que peu avec l’emplacement de l’objet. De plus, les termes masse et poids sont utilisés de manière interchangeable dans le langage courant; par exemple, nos dossiers médicaux indiquent souvent notre poids en kilogrammes, mais jamais dans les bonnes unités de newtons.

Idées fausses courantes : Masse vs. Poids

La masse et le poids sont souvent utilisés de manière interchangeable dans le langage courant. Cependant, en science, ces termes sont nettement différents les uns des autres. La masse est une mesure de la quantité de matière contenue dans un objet. La mesure typique de la masse est le kilogramme. Le poids, en revanche, est une mesure de la force de gravité agissant sur un objet. Le poids est égal à la masse d’un objet (\(m\)) multipliée par l’accélération due à la gravité (\(g\)). Comme toute autre force, le poids est mesuré en newtons \(N\).

En supposant que la masse d’un objet reste intacte, elle restera la même, quel que soit son emplacement. Cependant, comme le poids dépend de l’accélération due à la gravité, le poids d’un objet peut changer lorsque l’objet entre dans une région avec une gravité plus forte ou plus faible. Par exemple, l’accélération due à la gravité sur la Lune est \(1.67\,m/s^{2}\) (ce qui est bien inférieur à l’accélération due à la gravité sur Terre, \(9.81\,m/s^{2}\)). Si vous mesuriez votre poids sur Terre, puis que vous mesuriez votre poids sur la Lune, vous constateriez que vous pesez beaucoup moins, même si vous n’avez pas l’air plus maigre. C’est parce que la force de gravité est plus faible sur la Lune. En fait, quand les gens disent qu’ils perdent du poids, ils veulent vraiment dire qu’ils perdent de la masse (ce qui les amène à moins peser).

Exemple : Quelle accélération une personne peut-elle produire en poussant une tondeuse à gazon ?

Supposons que la force externe résultante (poussée moins frottement) exercée sur une tondeuse à gazon soit de \(51\,N\) parallèlement au sol. La masse de la tondeuse est de \(24\,kg\). Quelle est son accélération?

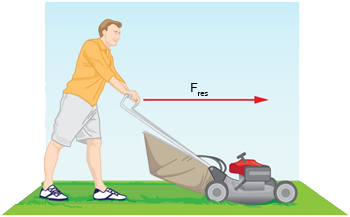
Fig. 9.6 La force résultante sur une tondeuse à gazon est de \(51\,N\) vers la droite. À quelle vitesse la tondeuse à gazon accélère-t-elle vers la droite ? (crédit : openstax.org)

stratégie

Depuis \(\vec{F}_{res}\) et \(m\) sont données, l’accélération peut être calculée directement à partir de la deuxième loi de Newton comme indiqué dans \(\vec{F}_{res}= m\cdot\vec{a}\).

solution

L’amplitude de l’accélération \(\vec{a}\) est \(a=\dfrac{F_{res}}{m}\). La saisie de valeurs connues donne:

\[a=\dfrac{51\,N}{24\,kg}=\dfrac{51\,kg\cdot m/s^{2}}{24\,kg}=2.1\,m/s^{2}\]

discussion

La direction de l’accélération est la même que celle de la force résultante, qui est parallèle au sol. Il n’y a aucune information donnée dans cet exemple sur les forces externes individuelles agissant sur le système, mais nous pouvons dire quelque chose sur leurs magnitudes relatives. Par exemple, la force exercée par la personne qui pousse la tondeuse doit être supérieure au frottement opposé au mouvement (puisque nous savons que la tondeuse avance), et les forces verticales doivent s’annuler s’il n’y a pas d’accélération dans le sens vertical (le la tondeuse se déplace uniquement horizontalement). L’accélération trouvée est suffisamment petite pour être raisonnable pour une personne poussant une tondeuse. Un tel effort ne durerait pas trop longtemps car la vitesse maximale de la personne serait bientôt atteinte.

Exemple : Quelle force de poussée accélère ce train monté sur une fusée ?

Avant les vols spatiaux transportant des astronautes, des trains équipés de fusées (trains-fusées) étaient utilisés pour tester des avions, des équipements de missiles et des effets physiologiques sur des sujets humains à grande vitesse. Ils consistaient en une plate-forme montée sur un ou deux rails et propulsée par plusieurs roquettes. Calculez l’amplitude de la force exercée par chaque fusée, appelée sa poussée \(\vec{T}\), pour le système de propulsion à quatre fusées illustré à la figure ci-dessous. L’accélération initiale du traîneau est \(49\,m/s^{2}\) la masse du système est de \(2100\,kg\) et la force de frottement s’opposant au mouvement est connue pour être de \(650\,N\).

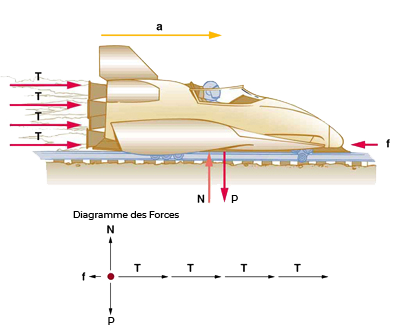
Fig. 9.7 Le train subit une poussée des fusées qui l’accélère vers la droite. Chaque fusée crée une poussée identique \(\vec{T}\). Comme dans d’autres situations où il n’y a qu’une accélération horizontale, les forces verticales s’annulent. Le sol exerce une force ascendante \(\vec{N}\) sur le système de grandeur égale et de sens opposé à son poids, \(\vec{P}\). Le système ici est le traîneau, ses fusées et son pilote, donc aucune des forces entre ces objets n’est prise en compte. La flèche représentant le frottement (\(\vec{f}\)) est dessiné plus grand que l’échelle. (crédit : openstax.org)

stratégie

Bien qu’il y ait des forces agissant verticalement et horizontalement, nous supposons que les forces verticales s’annulent car il n’y a pas d’accélération verticale. Cela nous laisse avec seulement des forces horizontales et un problème unidimensionnel plus simple. Les directions sont indiquées par des signes plus ou moins, la droite étant prise comme direction positive. Voir le diagramme des forces sur la figure.

solution

Puisque l’accélération, la masse et la force de frottement sont données, nous partons de la deuxième loi de Newton et cherchons des moyens de trouver la poussée des moteurs. Puisque nous avons défini la direction de la force et de l’accélération comme agissant à droite, nous devons considérer uniquement les grandeurs de ces quantités dans les calculs. Par conséquent, nous commençons par

\[\vec{F}_{res}= m\cdot\vec{a}\]

où \(\vec{F}_{res}\) est la force résultante le long de la direction horizontale. On voit sur la figure que les poussées du moteur s’ajoutent, tandis que le frottement s’oppose à la poussée. Sous forme d’équation, la force externe résultante est

\[\vec{F}_{res}= 4\vec{T}-\vec{f}\]

Substituer ceci dans la deuxième loi de Newton donne

\[\vec{F}_{res}= m\cdot\vec{a}=4\vec{T}-\vec{f}\]

En utilisant un peu d’algèbre, nous résolvons pour la poussée totale \(4 T\):

\[4\vec{T}=m\cdot\vec{a}+\vec{f}\]

La substitution de valeurs connues donne la poussée totale

\[4T=(m\cdot a)+f=(2100\,kg\cdot 49\,m/s^{2})+650\,N=2,6\cdot 10^{4}\,N\]

discussion

Les chiffres sont assez importants, le résultat pourrait donc vous surprendre. Des expériences comme celle-ci ont été réalisées au début des années 1960 pour tester les limites de l’endurance humaine et la configuration conçue pour protéger les sujets humains lors des éjections d’urgence des chasseurs à réaction. Des vitesses de \(1000\,km/h\) ont été obtenues, avec des accélérations de \(45g\). (Rappelons que \(g\), l’accélération due à la gravité, est de \(9,80\,m/s^{2}\). Quand on dit qu’une accélération est de \(45g\), c’est \(45 \times 9,80\,m/s^{2}\), qui est approximativement \(440\,m/s^{2}\).) Alors que les sujets vivants ne sont plus utilisés, des vitesses terrestres de \(10'000\,km/h\) ont été obtenues avec des fusées montées sur rail.

La deuxième loi du mouvement de Newton est plus qu’une définition; c’est une relation entre accélération, force et masse. Cela peut nous aider à faire des prédictions. Chacune de ces quantités physiques peut être définie indépendamment, de sorte que la deuxième loi nous dit quelque chose de fondamental et universel sur la nature. La section suivante présente la troisième et dernière loi du mouvement.