6.2. Équations de la cinématique#
Les équations cinématiques du M.R.U.A. sont les quatre équations suivantes :
Équations de la cinématique
Les quatre équations de la cinématique :
La démonstration de ces équations est expliquée dans le chapitre suivant.
Quelle équation cinématique utiliser ?#
Il faut trouver l’équation cinématique qui contient à la fois la variable recherchée et trois autre variables cinématiques connues. Ainsi on peut trouver directement la variable recherchée à partir de l’équation cinématique choisie.
Par exemple, on suppose qu’on donne un coup de pied dans un livre posé sur le sol de telle sorte que sa vitesse initiale vaut \(v_{0}=5\,m/s\). Pendant la durée \(t=3\,s\), le livre glisse sur le sol en parcourant la distance \(\Delta x=8\,m\). En supposant que le mouvement est rectiligne uniformément accéléré, on peut utiliser ici l’équation cinématique \(\Delta x=\dfrac{1}{2}a\cdot t^{2}+v_{0}\cdot t\) pour déterminer l’accélération du livre \(a\) - supposée constante - puisque les trois autres variables \(\Delta x\), \(v_{0}\) et \(t\) sont connues.
Astuce
Dans chaque équation cinématique, il ne manque qu’une seule des variables cinématiques \(\Delta x\), \(t\), \(v_{0}\), \(v(t)\), \(a\).
Pour choisir l’équation cinématique qui convient au problème posé, il faut repérer la variable qui n’est ni donnée, ni demandée. Dans l’exemple ci-dessus, la vitesse finale \(v\) du livre n’est ni donnée, ni demandée, il faut donc choisir l’équation où elle n’apparaît pas. L’équation cinématique \(\Delta x=\dfrac{1}{2}a\cdot t^{2}+v_{0}\cdot t\) ne contient pas \(v(t)\), c’est donc la bonne équation pour déterminer l’accélération \(a\).
Quelles sont les difficultés majeures avec les équations cinématiques ?#
On oublie souvent que ces équations cinématiques ne sont vraies que lorsque l’accélération est constante sur l’intervalle de temps considéré.
Parfois, une variable connue n’est pas explicitement donnée dans un problème, mais elle peut être évoquée implicitement avec des expressions spécifiques. Par exemple, démarre au repos signifie \(v_{0}=0\), lâché signifie aussi \(v_{0}=0\), et s’arrête signifie \(v(t)=0\). De plus, la valeur de l’accélération de la pesanteur est \(g=9.81\,m/s^{2}\), cette dernière est rarement donnée dans les problèmes qui concernent un projectile en chute libre.
On oublie souvent que toutes les variables cinématiques - \(\Delta x\), \(v_{0}\), \(v(t)\), \(a\) - excepté \(t\) - peuvent être négatives. L’oubli d’un signe négatif est une erreur très commune. Si la verticale est orientée positivement vers le haut, alors l’accélération de la pesanteur que subit un projectile en chute libre doit être négative: \(a_{g}=-9.81\,m/s^{2}\).
La troisième équation cinématique, \(\Delta x=\dfrac{1}{2}a\cdot t^{2}+v_{0}\cdot t\), peut nécessiter l’utilisation des solutions d’une équation du second degré (voir dans l’exemple 3 ci-dessous).
On oublie souvent que bien que l’on puisse choisir n’importe quel intervalle de temps dès lors que l’accélération est constante, les variables cinématiques utilisées dans les équations cinématiques doivent être cohérentes avec l’intervalle de temps considéré. Autrement dit, la vitesse initiale \(v_{0}\) doit être la vitesse de l’objet pour la position à laquelle il se trouve lorsque l’intervalle de temps \(t\) commence. De manière analogue, la vitesse finale \(v(t)\) doit être la vitesse de l’objet pour la position à laquelle il se trouve lorsque l’intervalle de temps \(t\) se termine.
Exemple 1 : Première équation cinématique : \(v(t)=a\cdot t+v_{0}\)
Un avion vol à la vitesse de \(70\,m/s\) puis décélère à un taux de \(1.50\,m/s^{2}\) pendant \(40\,s\) pour atterrir.

Quelle est sa vitesse finale ?
stratégie
Dessinez un croquis.
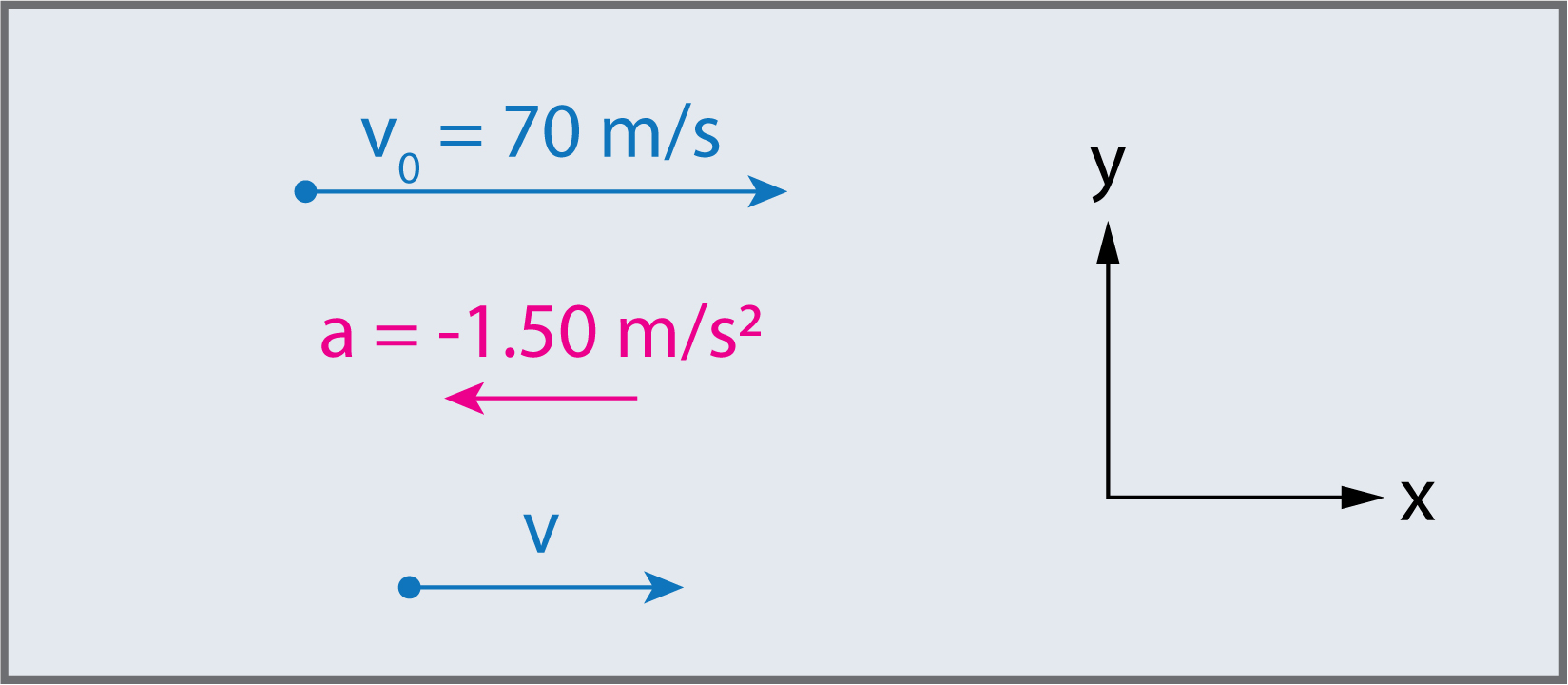
Nous dessinons le vecteur d’accélération dans la direction opposée au vecteur de vitesse car l’avion décélère.
solution
En supposant que la verticale est orientée positivement vers le haut, les variables connues sont :
La vitesse initiale de l’avion : \(v_{0}=70.0\,m/s\)
L’accélération : \(a_{g}=-1.50\,m/s^{2}\quad\) (Négative, car opposée à la direction de la vitesse)
Le temps pour atteindre la vitesse finale : \(t=40.0\,s\)
Dans cette situation, l’inconnue est la vitesse finale \(v(t)\) à \(t=40.0\,s\).
Comme on ne connaît pas le déplacement \(\Delta x\) et puisque le déplacement \(\Delta x\) n’est pas non plus demandé, on utilise la première équation cinématique: \(v(t)=a\cdot t+v_{0}\), dans laquelle \(\Delta x\) n’apparaît pas.
On a donc
discussion
La vitesse finale est bien inférieure à la vitesse initiale, comme souhaité lors d’un ralentissement, mais toujours positive. Avec les moteurs à réaction, l’inversion de poussée pourrait être maintenue suffisamment longtemps pour arrêter l’avion et commencer à le faire reculer. Cela serait indiqué par une vitesse finale négative, ce qui n’est pas le cas ici.
Exemple 2 : Deuxième équation cinématique : \(\Delta x=\dfrac{v(t)+v_{0}}{2}\cdot t\)
Un léopard court à \(6.20\,m/s\). En apercevant un mirage ressemblant à une antilope, il se met à accélérer pendant \(3.3\,s\) jusqu’à atteindre la vitesse de \(23.1\,m/s\).
Quelle distance le léopard a-t-il parcourue en passant de \(6.20\,m/s\) à\(23.1\,m/s\)?
solution
En supposant que le mouvement a lieu dans le sens positif, les variables connues sont :
la vitesse initiale du léopard: \(v_{0}=6.20\,m/s\)
La vitesse finale du léopard : \(v(t)=23.1\,m/s\)
Le temps pendant lequel le léopard accélère : \(t=3.3\,s\)
Puisqu’on ne connaît pas l’accélération \(a\) et qu’elle n’est pas demandée, on utilise la seconde équation cinématique sur la direction horizontale \(\Delta x=\dfrac{v(t)+v_{0}}{2}\cdot t\), dans laquelle \(a\) n’apparaît pas.
Exemple 3 : Troisième équation cinématique : \(\Delta x=\dfrac{1}{2}a\cdot t^{2}+v_{0}\cdot t\)
Une étudiante lassée de travailler sur les équations cinématiques jette son crayon verticalement vers le haut à \(18.3\,m/s\).
En combien de temps le crayon atteint-il le point situé à \(12.2\,m\) au dessus du point où il a été lancé ?
solution
En supposant que la verticale est orientée positivement vers le haut, les variables connues sont :
Puisqu’on ne connaît pas la vitesse finale \(v(t)\) et qu’elle n’est pas demandée, on utilise la troisième équation cinématique sur la direction verticale \(\Delta y=\dfrac{1}{2}a\cdot t^{2}+v_{0}\cdot t\), dans laquelle \(v(t)\) n’apparaît pas.
Jusqu’à présent, on a pu déduire l’expression de la variable inconnue assez simplement à partir de l’équation cinématique. Ici, déduire l’expression de \(t\) si aucun terme ne s’annule est un peu plus ardu. En effet, comme on peut le voir en remplaçant les grandeurs connues par leurs valeurs numériques, on est en présence d’une équation du second degré:
On passe tous les termes du même côté de l’équation de façon à pouvoir résoudre cette équation du second degré plus simplement. En soustrayant \(12.2\,m\) des deux côtés, on obtient:
Il faut donc maintenant résoudre cette équation du second degré pour la variable \(t\). Les solutions d’une équation de la forme \(at^{2}+bt+c=0\) sont de la forme \(t=\dfrac{-b\pm\sqrt{b^{2}-4ac}}{2a}\). Ici, on a \(a=\dfrac{1}{2}(-9.81\,m/s^{2})\), \(b=18.3\,m/s\) et \(c=-12.2\,m\).
Les solutions sont donc:
Comme il y a un signe plus ou moins dans l’expression de \(t\), il y a deux solutions possibles: une en utilisant le \(+\) et une en utilisant le \(-\). Le calcul des solutions donne les intervalles de temps suivants:
discussion
Il y a deux solutions positives puisqu’il y a deux instants pour lesquels le crayon se trouve à une hauteur de \(12.2\,m\) au dessus du point de lancement.
L’intervalle de temps le plus petit correspond à la montée du crayon, c’est à dire à un déplacement direct de \(12.2\,m\).
L’intervalle de temps le plus grand correspond au temps mis par le crayon pour monter, atteindre son altitude maximale, puis tomber en repassant par une altitude correspondant à un déplacement de \(12.2\,m\).
Par conséquent, il faut choisir l’intervalle de temps le plus petit \(t=0.869\,s\) pour avoir la réponse à la question En combien de temps le crayon atteint-il le point situé à \(12.2\,m\) au dessus du point où il a été lancé ?
Lorsque l’équation du second degré donne un intervalle de temps négatif et un intervalle de temps positif, l’objet en question, lui, ne réalise son déplacement qu’une fois, après avoir été lancé. On choisit donc l’intervalle de temps positif et on néglige la solution négative.
En effet, l’intervalle de temps négatif fait référence à un instant antérieur au lancement de l’objet où il aurait occupé la position finale. Autrement dit, cela reviendrait à considérer que l’objet était sur sa trajectoire avant d’être lancé et qu’il passe par le point de lancement avec la vitesse donnée comme vitesse initiale.
Exemple 4 : Quatrième équation cinématique : \(v(t)^{2}-v_{0}^{2}=2a\cdot\Delta x\)
Un motard roule à la vitesse de \(23.4\,m/s\). Voyant qu’il s’approche d’un embouteillage, il décide de ralentir sur une distance de \(50.2\,m\) avec une décélération constante de valeur \(3.20\,m/s^{2}\). On suppose que le mouvement du motard est rectiligne sur l’ensemble du trajet et qu’il avance continuellement.
Quelle est la nouvelle vitesse du motard après avoir ralenti sur \(50.2\,m\) ?
solution
En supposant que le mouvement a lieu dans le sens positif, les variables connues sont :
Puisqu’on ne connaît pas l’intervalle de temps \(t\) et qu’il n’est pas demandé, on utilise la quatrième équation cinématique sur la direction horizontale \(v(t)^{2}-v_{0}^{2}=2a\cdot\Delta x\), dans laquelle \(t\) n’apparaît pas. on exprime la vitesse finale : \(v_{fin}=\pm\sqrt{2a\cdot\Delta x+v_{0}^{2}}\).
On remarque qu’en prenant la racine carrée, on obtient deux réponses possibles: l’une positive, l’autre négative. Puisque le motard avance continuellement dans le sens considéré positif, on choisit donc la réponse positive \(v_{fin}=+\sqrt{2a\cdot\Delta x+v_{0}^{2}}\).
On obtient donc l’expression numérique suivante :
