Questions conceptuelles

2.3. Questions conceptuelles#

Question 1

Un élève écrit : “Un oiseau qui plonge sur sa proie a une vitesse de $-10\,m/s$”.
Quel est le problème avec la déclaration de l’élève ? Qu’est-ce que l’élève a réellement décrit ?
Expliquez.

réponse

Si l’oiseau plonge, c’est que la direction de son mouvement est vertical dirigé vers le bas (l’axe de référence est dirigé vers le bas). Or si la vitesse de l’oiseau est négative, cela signifie que la direction du mouvement de l’oiseau est inverse de la direction positive de l’axe, donc l’oiseau monte !

Question 2

L’accélération est le changement de vitesse dans le temps. Compte tenu de ces informations, l’accélération est-elle un vecteur ou une quantité scalaire ?
Expliquez.

réponse

Le changement de vitesse est un vecteur et le temps un scalaire. Si on divise un vecteur par un scalaire, on obtient encore un vecteur, de même direction mais avec une plus petite amplitude (longueur).

Question 3

Une prévision météorologique indique que la température devrait être $-5°C$, le jour suivant. Cette température est-elle un vecteur ou une grandeur scalaire ?
Expliquez.

réponse

La température n’a pas besoin de direction pour être définie. C’est donc un scalaire

Question 4

Lequel des éléments suivants est un vecteur: la taille d’une personne, l’altitude du mont Everest, l’âge de la Terre, le point d’ébullition de l’eau, l’accélération de la gravité, le coût de ce livre, la population de la Terre ?

réponse

l’accélération de la gravité

Question 5

Quel est le point commun entre les vecteurs et les scalaires ? Comment diffèrent-ils ?

réponse

Les deux possèdent une amplitude, mais le vecteur a besoin d’une direction en plus. A 2 (ou plus) dimensions, le vecteur possède plusieurs coordonnées, alors que le scalaire n’a qu’une valeur (identique dans toutes les dimensions)

Question 6

Deux campeurs dans un parc national partent en randonnée de leur chalet au même endroit sur un lac, chacun empruntant un chemin différent, comme illustré ci-dessous. La distance totale parcourue le long du chemin $1$ est de $7.5\,km$ et celle le long du chemin $2$ est de $8.2\,km$.
Quel est le déplacement final de chaque campeur ?

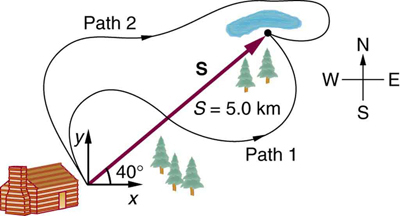
réponse

De $S=5\,km$ à $40°$ Nord-Est,
ou :

\[\begin{split}\overrightarrow{S}= \begin{pmatrix} S_{x}\\ S_{y} \end{pmatrix}= \begin{pmatrix} 5\cdot\cos(40)\\ 5\cdot\sin(40) \end{pmatrix}\end{split}\]

Question 7

Si on dit à un pilote d’avion de parcourir $123\,km$ en ligne droite pour se rendre de San Francisco à Sacramento, expliquez pourquoi il pourrait se retrouver n’importe où sur le cercle illustré à la figure ci-dessous. De quelles autres informations aurait-il besoin pour se rendre à Sacramento ?

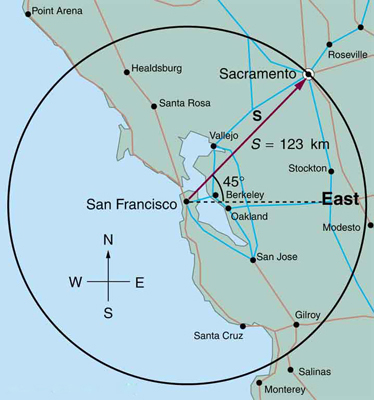
réponse

Il lui manque la direction de $45°$ Nord-Est. Sans cette information, le pilote peut partir dans n’importe quelle direction.

Question 8

Est-il possible d’ajouter un scalaire à un vecteur ?
Est-il possible de multiplier un scalaire avec un vecteur ?

réponse

Non
Oui; par exemple $5\cdot\overrightarrow{7}\,N=\overrightarrow{35}\,N$

Question 9

Supposons que vous fassiez deux pas $A$ et $B$ (c’est-à-dire deux déplacements non nuls).

Dans quelles circonstances pouvez-vous vous retrouver à votre point de départ ? Plus généralement, dans quelles circonstances deux vecteurs non nuls peuvent-ils s’additionner pour donner zéro ?
Est-ce que la distance maximale que vous pouvez parcourir depuis le point de départ est la somme des longueurs des deux pas $A+B$ ?

réponse

Lorsque les deux vecteurs ont la même intensité (même valeur absolue), mais des directions opposées $\overrightarrow{A}+\overrightarrow{B}=\overrightarrow{A}+(-\overrightarrow{A})=0.
La distance maximale sera de $\lVert \vec{A} \rVert +\lVert \vec{B} \rVert$

Question 10

Si vous faites deux pas de tailles différentes, pouvez-vous vous retrouver à votre point de départ? Plus généralement, deux vecteurs d’amplitudes différentes peuvent-ils s’additionner pour donner zéro ? Est-ce que trois vecteur (ou plus) le peuvent ?

réponse

Non pour 2, Oui pour 3.

Question 11

Donner un exemple de vecteur non nul dont une composante est nulle.

réponse

Le vecteur accélération terrestre $\vec{g}$ qui est uniquement vertical. Sa composante horizontale est toujours nulle :

\[\begin{split}\overrightarrow{g}= \begin{pmatrix} g_{x}\\ g_{y} \end{pmatrix}= \begin{pmatrix} 0\\ 9.81 \end{pmatrix} m/s^{2}\end{split}\]

Question 12

Expliquez pourquoi un vecteur ne peut pas avoir une composante supérieure à sa propre amplitude.

réponse

Car l’amplitude d’un vecteur se calcul avec Pythagore.
Si

\[\begin{split}\overrightarrow{A}= \begin{pmatrix} A_{x}\\ A_{y} \end{pmatrix}\end{split}\]

alors son amplitude vaut : $\Vert\overrightarrow{A}\Vert=\sqrt{A_{x}^{2}+A_{y}^{2}}\geqslant A_{x}$ (ou $A_{y}$)