Applications des lois de Newton

10.2. Applications des lois de Newton#

Il existe de nombreuses applications intéressantes des lois du mouvement de Newton, dont quelques-unes sont présentées dans cette section. Elles servent également à illustrer certaines subtilités supplémentaires de la physique et à aider à développer des compétences en résolution de problèmes.

Exemple : Force de traînée sur une barge

Supposons que deux remorqueurs poussent une barge sous différents angles, comme illustré à la Fig. 10.2. Le premier remorqueur exerce une force de $2.7\cdot 10^5\,N$ dans la direction $x$, et le second remorqueur exerce une force de $3.6\cdot 10^5\,N$ dans la direction $y$.

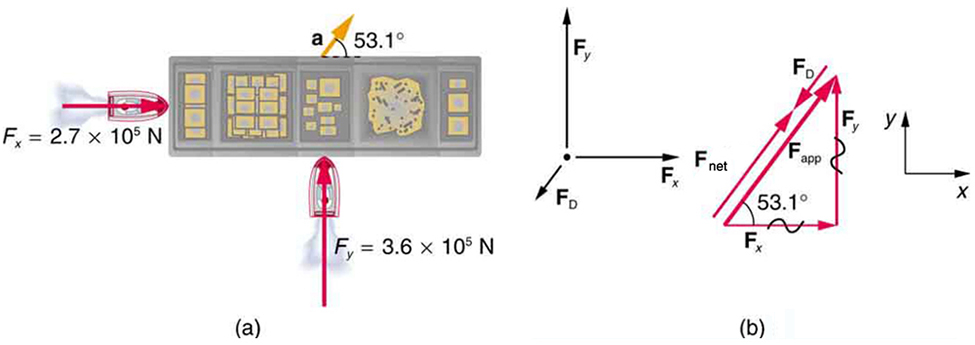
../../_images/Barge.jpg — Fig. 10.2 (a) Une vue de dessus de deux remorqueurs poussant sur une barge. (b) Le diagramme de corps libre pour le navire contient uniquement les forces agissant dans le plan de l’eau. Il omet les deux forces verticales — le poids de la barge et la force de flottaison de l’eau qui la soutient s’annulent et ne sont pas montrés. Puisque les forces appliquées sont perpendiculaires, les axes $x$ et $y$ sont dans la même direction que $F_{x}$ et $F_{y}$. Le problème devient rapidement un problème unidimensionnel le long de la direction de Fapp, puisque la friction est dans la direction opposée à $F_{app}$. Si la masse de la barge est de $5.0\cdot 10^{6}\,kg$ et son accélération est observée être de $7.5\cdot 10^{-2}\,m/s^2$ dans la direction montrée, quelle est la force de traînée de l’eau sur la barge résistant au mouvement ? (Note : la force de traînée est une force de friction exercée par les fluides, tels que l’air ou l’eau. La force de traînée s’oppose au mouvement de l’objet.)#

stratégie

Les directions et magnitudes de l’accélération et des forces appliquées sont données à la Fig. 10.2(a). Nous définirons la force totale des remorqueurs sur la barge comme $F_{app}$ de sorte que :

\[F_{app} = F_x + F_y\]

Puisque la barge a un fond plat, la traînée de l’eau $F_D$ sera dans la direction opposée à $F_{app}$, comme montré dans le diagramme de corps libre à la Fig. 10.2(b).
Le système d’intérêt ici est la barge, puisque les forces sur elle sont données ainsi que son accélération. Notre stratégie est de trouver l’amplitude et la direction de la force appliquée nette $F_{app}$, puis d’appliquer la seconde loi de Newton pour résoudre la force de traînée $F_D$.

solution

Puisque $F_x$ et $F_y$ sont perpendiculaires, l’amplitude et la direction de $F_{app}$ sont facilement trouvées. D’abord, l’amplitude résultante est donnée par le théorème de Pythagore :

\[F_{app} = \sqrt{(2.7\cdot 10^5 N)^2 + (3.6\cdot 10^5 N)^2} = 4.5\cdot 10^5 N\]

L’angle est donné par

\[\theta = \tan^{-1}\left(\frac{F_y}{F_x}\right) = \tan^{-1}\left(\frac{3.6\cdot 10^5 N}{2.7\cdot 10^5 N}\right) = 53°\]

ce que nous savons, à cause de la première loi de Newton, être la même direction que l’accélération. $F_D$ est dans la direction opposée de $F_{app}$, puisqu’elle agit pour ralentir l’accélération. Par conséquent, la force externe nette est dans la même direction que $F_{app}$, mais sa magnitude est légèrement inférieure à $F_{app}$. Le problème est maintenant unidimensionnel. D’après la Fig. 10.2(b), nous pouvons voir que

\[F_{net} = F_{app} - F_D\]

Mais la seconde loi de Newton énonce que

\[F_{net} = ma\]

Ainsi,

\[F_{app} - F_D = ma\]

Cela peut être résolu pour l’amplitude de la force de traînée de l’eau $F_D$ en termes de quantités connues :

\[F_D = F_{app} - ma = (4.5\cdot 10^5 N) - (5.0\cdot 10^6 kg)(7.5\cdot 10^{-2} m/s^2) = 7.5\cdot 10^4 N\]

La direction de $F_D$ a déjà été déterminée comme étant dans la direction opposée à $F_{app}$, ou à un angle de 53º au sud de l’ouest.

discussion

Les nombres utilisés dans cet exemple sont raisonnables pour une barge modérément grande. Il est certainement difficile d’obtenir des accélérations plus grandes avec des remorqueurs, et des vitesses faibles sont souhaitables pour éviter de faire courir la barge contre les quais. La traînée est relativement petite pour une coque bien conçue à faibles vitesses, ce qui est cohérent avec la réponse à cet exemple, où $F_D$ est inférieur à 1/600^ème du poids du navire.

Dans un exemple précédent, concernant un funambule, nous avons remarqué que les tensions dans les câbles soutenant une masse étaient égales uniquement parce que les angles de chaque côté étaient égaux. Considérons l’exemple suivant, où les angles ne sont pas égaux ; cela implique un peu plus de trigonométrie.

Exemple : Différentes tensions sous différents angles

Considérez le feu de circulation (masse de $15.0\,kg$) suspendu par deux fils comme illustré dans la Fig. 10.3. Trouvez la tension dans chaque fil, en négligeant les masses des fils.

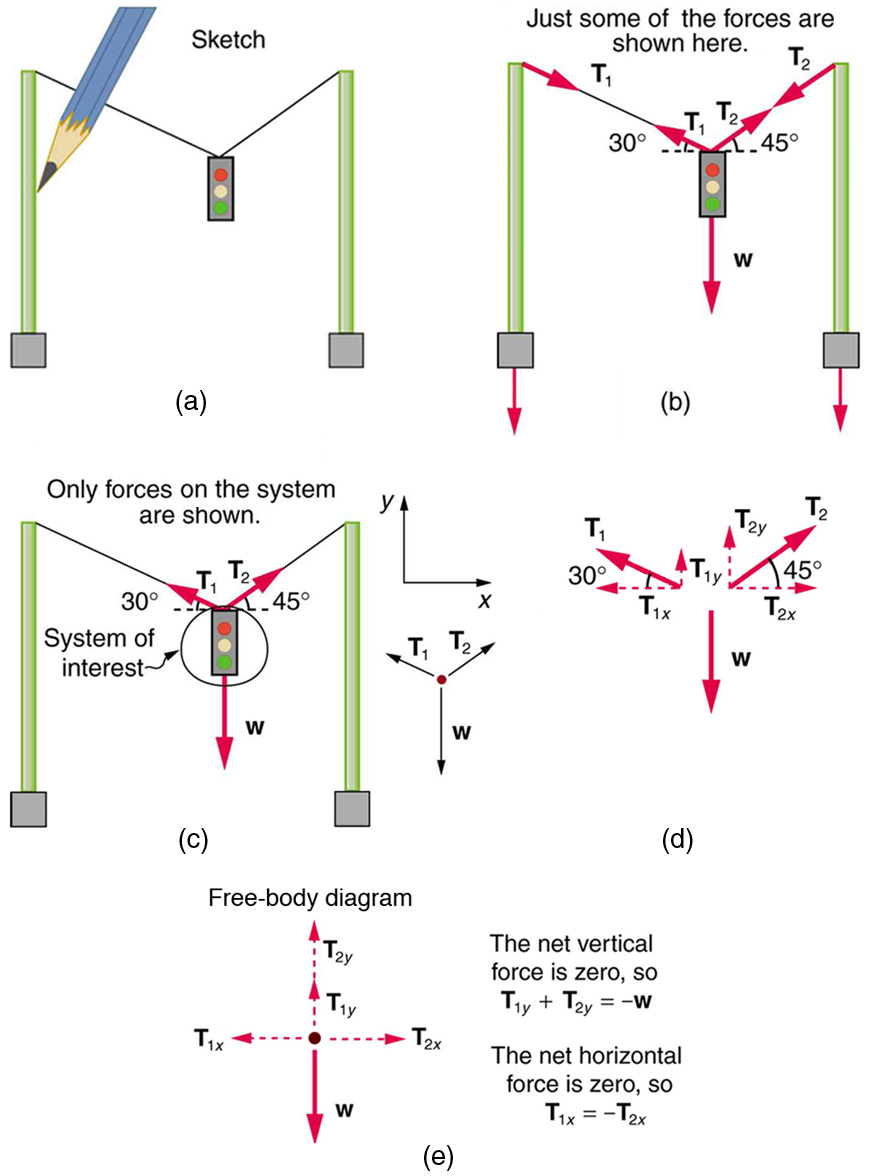
Un croquis d'un feu de circulation suspendu par deux fils soutenus par deux poteaux est montré. (b) Certaines forces sont représentées dans ce système. La tension $T_{1}$ tirant le haut du poteau gauche est indiquée par une flèche vectorielle le long du fil gauche depuis le haut du poteau, et une tension opposée mais égale $T_{1}$ est montrée par la flèche pointant vers le haut le long du fil gauche là où il est attaché au feu ; le fil forme un angle de trente degrés avec l'horizontal. La tension $T_{2}$ est indiquée par une flèche vectorielle pointant vers le bas depuis le haut du poteau droit le long du fil droit, et une tension opposée mais égale $T_{2}$ est montrée par la flèche pointant vers le haut le long du fil droit, qui forme un angle de quarante-cinq degrés avec l'horizontal. Le feu de circulation est suspendu à l'extrémité inférieure des fils, et son poids W est indiqué par une flèche vectorielle agissant vers le bas. (c) Le feu de circulation est le système d'intérêt. La tension $T_{1}$ partant du feu de circulation est indiquée par une flèche le long du fil formant un angle de trente degrés avec l'horizontal. La tension $T_{2}$ partant du feu de circulation est indiquée par une flèche le long du fil formant un angle de quarante-cinq degrés avec l'horizontal. Le poids W est indiqué par une flèche vectorielle pointant vers le bas depuis le feu de circulation. Un diagramme de corps libre est montré avec trois forces agissant sur un point. Le poids W agit vers le bas ; $T_{1}$ et $T_{2}$ agissent à un angle avec la verticale. (d) Les forces sont montrées avec leurs composantes T_{1y} et T_{2y} pointant verticalement vers le haut.T_{1}x pointe le long de la direction négative de x, T_{2x} pointe le long de la direction positive de x, et le poids W pointe verticalement vers le bas. (e) Les forces verticales et horizontales sont montrées séparément. Les forces verticales T_{1}y et T_{2y} sont indiquées par des flèches vectorielles agissant le long d'une ligne verticale pointant vers le haut, et le poids W est indiqué par une flèche vectorielle agissant vers le bas. La force verticale nette est nulle, donc T_{1}y plus T_{2y} est égal à W. D'autre part, T_{2x} est indiqué par une flèche pointant vers la droite, et T_{1}x est indiqué par une flèche pointant vers la gauche. La force horizontale nette est nulle, donc T_{1}x est égal à T_{2x}. — Fig. 10.3 Un feu de circulation est suspendu par deux fils. (b) Certaines des forces impliquées. (c) Seules les forces agissant sur le système sont montrées ici. Le diagramme de corps libre pour le feu de circulation est également montré. (d) Les forces projetées sur les axes vertical (y) et horizontal (x). Les composantes horizontales des tensions doivent s’annuler, et la somme des composantes verticales des tensions doit égaler le poids du feu de circulation. (e) Le diagramme de corps libre montre les forces verticales et horizontales agissant sur le feu de circulation.#

stratégie

Le système d’intérêt est le feu de circulation, et son diagramme de corps libre est montré dans la Fig. 10.3(c). Les trois forces impliquées ne sont pas parallèles et doivent donc être projetées sur un système de coordonnées. Le système de coordonnées le plus pratique a un axe vertical et un horizontal, et les projections vectorielles sur celui-ci sont montrées dans la partie (d) de la figure. Il y a deux inconnues dans ce problème ($T_{1}$ et $T_{2}$), donc deux équations sont nécessaires pour les trouver. Ces deux équations proviennent de l’application de la deuxième loi de Newton le long des axes vertical et horizontal, notant que la force externe nette est nulle le long de chaque axe car l’accélération est nulle.

solution

Considérez d’abord l’axe horizontal ou $x$ :

\[F_{net_{x}}=T_{2x}−T_{1x}=0.\]

Ainsi, comme vous pourriez vous y attendre,

\[T_{1}=T_{2}\]

Cela nous donne la relation suivante entre $T_{1}$ et $T_{2}$ :

\[T_{1}cos(30°)=T_{2}cos(45°)\]

Ainsi,

\[T_{2}=\dfrac{cos(30°}{cos(45°)}T_1=(1.225)T_{1}\]

Notez que $T_{1}$ et $T_{2}$ ne sont pas égaux dans ce cas, car les angles de chaque côté ne sont pas égaux. Il est raisonnable que $T_{2}$ soit plus grand que $T_{1}$, car il est exercé plus verticalement que $T_{1}$.

Considérez maintenant les composantes de force le long de l’axe vertical ou y :

\[F_{net_{y}}=T_{1y}+T_{2y}−w=0\]

Cela implique

\[T_{1y}+T_{2y}=w\]

En substituant les expressions pour les composantes verticales, nous obtenons

\[T_{1}sin(30°)+T_{2}sin(45°)=w\]

Il y a deux inconnues dans cette équation, mais substituer l’expression pour $T_{2}$ en termes de $T_{1}$ réduit cela à une équation avec une inconnue :

\[T_{1}(0.500)+(1.225)T_{1}(0.707)=w=mg\]

ce qui donne

\[(1.366)T_{1}=(15.0\,kg)(9.81\,m/s^{2})\]

En résolvant cette dernière équation, nous obtenons l’amplitude de $T_{1}$ pour être

\[T_{1}=108\,N\]

Finalement, l’amplitude de $T_{2}$ est déterminée en utilisant la relation entre eux, $T_{2}=1.225\cdot T_{1}$, trouvée ci-dessus. Ainsi, nous obtenons

\[T_{2}=132\,N\]

discussion

Les deux tensions seraient plus grandes si les deux fils étaient plus horizontaux, et elles seront égales si et seulement si les angles de chaque côté sont les mêmes (comme c’était le cas dans l’exemple précédent d’un funambule).

Le pèse-personne est un excellent exemple d’une force normale agissant sur un corps. Il fournit une lecture quantitative de combien il doit pousser vers le haut pour supporter le poids d’un objet. Mais pouvez-vous prédire ce que vous verriez sur le cadran d’un pèse-personne si vous vous teniez dessus pendant un trajet en ascenseur ? Verrez-vous une valeur supérieure à votre poids lorsque l’ascenseur démarre ? Et lorsque l’ascenseur monte à vitesse constante : le pèse-personne indiquera-t-il toujours plus que votre poids au repos ? Considérez l’exemple suivant.

Exemple : Qu’indique une balance dans un ascenseur ?

La Fig. 10.4 montre un homme de $75.0\,kg$ debout sur une balance de salle de bain dans un ascenseur. Calculez l’indication de la balance :

Si l’ascenseur accélère vers le haut à un taux de $1.20\,m/s^2$
Si l’ascenseur se déplace vers le haut à une vitesse constante de $1\,m/s$

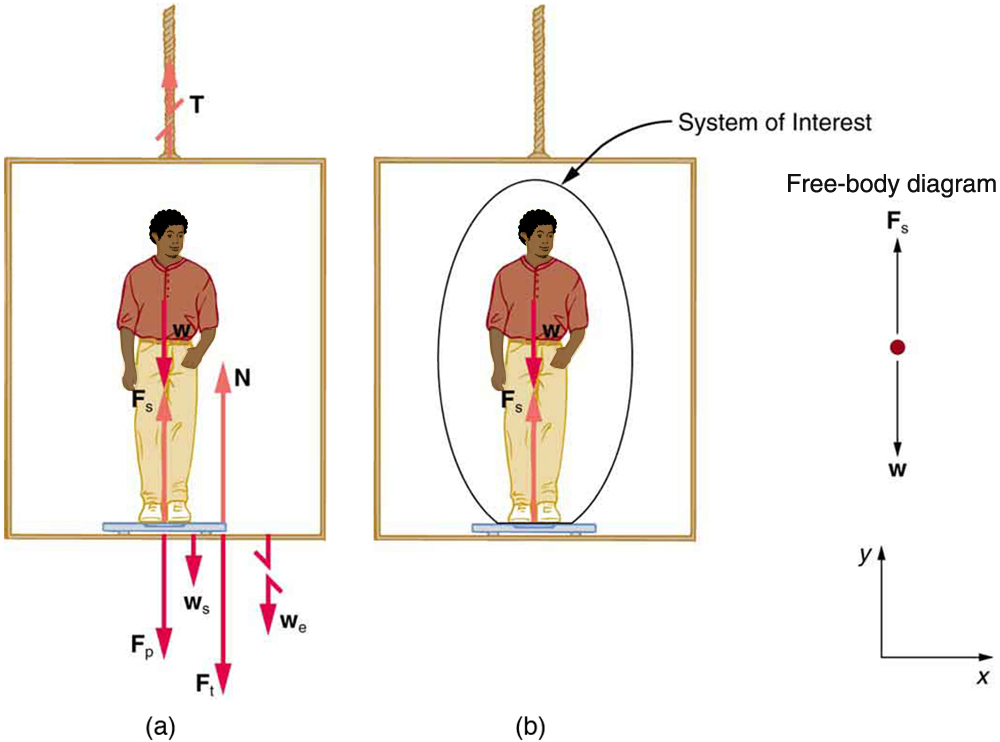
../../_images/Ascenseur.jpg — Fig. 10.4 (a) Les différentes forces agissant lorsqu’une personne se tient sur une balance de salle de bain dans un ascenseur. Les flèches sont approximativement correctes lorsque l’ascenseur accélère vers le haut - les flèches brisées représentent des forces trop grandes pour être dessinées à l’échelle. $T$ représente le poids de la balance, $w_e$ est le poids de l’ascenseur, $F_s$ est la force de la balance sur la personne, $F_p$ est la force de la personne sur la balance, $F_t$ est la force de la balance sur le sol de l’ascenseur, et $N$ est la force du sol vers le haut sur la balance. (b) Le diagramme de corps libre montre uniquement les forces externes agissant sur le système désigné d’intérêt - la personne.#

stratégie

Si la balance est précise, sa lecture égalera $F_p$, l’amplitude de la force que la personne exerce vers le bas sur elle. La Fig. 10.4(a) montre les nombreuses forces agissant sur l’ascenseur, la balance et la personne. Cela rend ce problème unidimensionnel beaucoup plus redoutable que si la personne est choisie comme système d’intérêt et qu’un diagramme de corps libre est dessiné comme dans la Fig. 10.4(b). L’analyse du diagramme de corps libre en utilisant les lois de Newton peut produire des réponses aux deux parties (a) et (b) de cet exemple, ainsi qu’à certaines autres questions qui pourraient survenir. Les seules forces agissant sur la personne sont son poids w et la force ascendante de la balance Fs. Selon la troisième loi de Newton, $F_p$ et $F_s$ sont égaux en magnitude et opposés en direction, de sorte que nous devons trouver Fs pour trouver ce que la balance lit. Nous pouvons le faire, comme d’habitude, en appliquant la deuxième loi de Newton,

\[F_{net} = ma\]

À partir du diagramme de corps libre, nous voyons que $F_{net} = F_s - w$, de sorte que

\[F_s - w = ma\]

En résolvant pour $F_s$, nous obtenons une équation avec seulement une inconnue :

\[F_s = ma + w\]

ou, parce que $w = mg$, simplement

\[F_s = ma + mg\]

Aucune hypothèse n’a été faite sur l’accélération, et donc cette solution devrait être valide pour une variété d’accélérations en plus de celles de cet exercice.

solution

Solution pour 1.

Dans cette partie du problème, $a = 1.20 \,m/s{^2}$, de sorte que

\[F_s = (75.0\,kg)(1.20\,m/s^{2}) + (75.0 \,kg)(9.81 \,m/s^{2})\]

ce qui donne

\[F_s = 825\,N\]

Solution pour 2.

Maintenant, que se passe-t-il lorsque l’ascenseur atteint une vitesse ascendante constante ? La balance lira-t-elle toujours plus que son poids ? Pour toute vitesse constante - vers le haut, vers le bas ou stationnaire - l’accélération est nulle car $a = \frac{\Delta v}{\Delta t}$, et $\Delta v = 0$. Ainsi,

\[F_s = ma + mg = 0 + mg\]

Maintenant,

\[F_s = (75.0\,kg)(9.81\,m/s^{2})\]

ce qui donne

\[F_s = 735 \,N\]

discussion

Discussion pour 1.

Que lirait la balance s’il était immobile ? Étant donné que son accélération serait nulle, la force de la balance serait égale à son poids :

\[F_{net} = F_s - F_s = ma = 0 = F_s - w = w = mg = (75.0 \,kg)(9.81 \,m/s^{2}) = 735\,N\]

Ainsi, la lecture de la balance dans l’ascenseur est supérieure à son poids de $735\,N$. Cela signifie que la balance pousse vers le haut sur la personne avec une force supérieure à son poids, comme elle doit le faire pour l’accélérer vers le haut. De toute évidence, plus l’accélération de l’ascenseur est grande, plus la lecture de la balance est grande, ce qui est conforme à ce que vous ressentez dans les ascenseurs accélérant rapidement par rapport à ceux accélérant lentement.

Discussion pour 2.

La lecture de la balance est de $735\,N$, ce qui équivaut au poids de la personne. Cela sera le cas chaque fois que l’ascenseur aura une vitesse constante - vers le haut, vers le bas ou stationnaire.

La solution de l’exemple précédent s’applique également à un ascenseur accélérant vers le bas, comme mentionné. Lorsqu’un ascenseur accélère vers le bas, l’accélération $a$ est négative, et la lecture de l’échelle est inférieure au poids de la personne, jusqu’à ce qu’une vitesse constante vers le bas soit atteinte, moment où la lecture de l’échelle redevient égale au poids de la personne. Si l’ascenseur est en chute libre et accélère vers le bas à $g$, alors la lecture de l’échelle sera nulle et la personne semblera être en apesanteur.

Intégration des Concepts : Lois de Newton sur le mouvement et la cinématique#

La physique est plus intéressante et plus puissante lorsqu’elle est appliquée à des situations générales impliquant plus qu’un ensemble étroit de principes physiques. Les lois du mouvement de Newton peuvent également être intégrées à d’autres concepts discutés précédemment dans ce texte pour résoudre des problèmes de mouvement. Par exemple, les forces produisent des accélérations, un sujet de cinématique, et donc la pertinence des chapitres précédents. Lors de l’approche des problèmes impliquant différents types de forces, d’accélérations, de vitesses et/ou de positions, suivez les étapes suivantes pour aborder le problème.

Stratégie de résolution de problèmes#

Étape 1.: Identifier quels principes physiques sont impliqués. Dresser la liste des données et des quantités à calculer vous permettra d’identifier les principes impliqués.
Étape 2.: Résoudre le problème en utilisant les stratégies déjà présentée dans ce cours. Si elles sont disponibles pour le sujet spécifique, vous devriez vous y référer. Vous devriez également vous référer aux sections du texte qui traitent d’un sujet particulier. L’exemple suivant illustre comment ces stratégies sont appliquées à un problème de concept intégré.

Exemple : Quelle force un joueur de football américain doit-il exercer pour atteindre sa vitesse maximale ?

Un joueur de football part du repos et accélère vers l’avant, atteignant une vitesse de $8.00\,m/s$ en $2.50\,s$.

Quelle était son accélération moyenne ?
Quelle force moyenne a-t-il exercée vers l’arrière sur le sol pour atteindre cette accélération ?

La masse du joueur est de $70.0\,kg$, et la résistance de l’air est négligeable.

stratégie

Pour résoudre un problème de concept intégré, nous devons d’abord identifier les principes physiques impliqués et les chapitres dans lesquels ils se trouvent. La partie 1. de cet exemple concerne l’accélération le long d’une ligne droite. Il s’agit d’un sujet de cinématique. La partie 2. traite de la force, un sujet de dynamique trouvé dans ce chapitre.

Les solutions suivantes à chaque partie de l’exemple illustrent comment les stratégies de résolution de problèmes spécifiques sont appliquées. Celles-ci impliquent d’identifier les connaissances et les inconnues, de vérifier si la réponse est raisonnable, et ainsi de suite.

solution

Solution pour 1.

Nous avons donné les vitesses initiale et finale (zéro et $8.00\,m/s$ vers l’avant) ; ainsi, le changement de vitesse est $\Delta v=8.00\,m/s$.
Nous avons donné le temps écoulé, donc $\Delta t=2.50\,s$. L’inconnue est l’accélération, qui peut être trouvée à partir de sa définition :

\[a=\dfrac{\Delta v}{\Delta t}\]

En substituant les valeurs connues, on obtient

\[a=\dfrac{8.00\,m/s^{2}}{2.50\,s}=3.20\,m/s^{2}\]

Solution pour 2.

Ici, on nous demande de trouver la force moyenne que le joueur exerce vers l’arrière pour obtenir cette accélération vers l’avant. En négligeant la résistance de l’air, cela serait égal en magnitude à la force externe nette sur le joueur, puisque cette force cause son accélération. Puisque nous connaissons maintenant l’accélération du joueur et sa masse donnée, nous pouvons utiliser la deuxième loi de Newton pour trouver la force exercée. C’est-à-dire,

\[F_{net}=ma.\]

En substituant les valeurs connues de $m$ et $a$, on obtient

\[F_{net}=(70.0\,kg)(3.20\,m/s^{2})=224\,N.\]

discussion

Discussion pour 1.

Il s’agit d’une accélération réalisable pour un athlète en bonne condition physique.

Discussion pour 2.

Cela représente une force moyenne raisonnable (cela revient à soulever une masse de $22.8\,kg$.)

Cet exemple illustré montre comment appliquer des stratégies de résolution de problèmes à des situations qui incluent des sujets de différents chapitres. La première étape est d’identifier les principes physiques impliqués dans le problème. La deuxième étape consiste à résoudre l’inconnue en utilisant des stratégies de résolution de problèmes familières. Ces stratégies se trouvent dans tout le texte, et de nombreux exemples résolus montrent comment les utiliser pour des sujets uniques. Vous trouverez ces techniques pour des problèmes de concepts intégrés utiles dans des applications de physique en dehors d’un cours de physique, telles que dans votre profession, dans d’autres disciplines scientifiques et dans la vie quotidienne. Les problèmes suivants renforceront vos compétences dans l’application large des principes physiques.

Applications des lois de Newton

Contents

10.2. Applications des lois de Newton#

Intégration des Concepts : Lois de Newton sur le mouvement et la cinématique#

Stratégie de résolution de problèmes#