1.4. Exactitude, précision et incertitude d’une mesure#
Exactitude#
La science est basée sur l’observation et l’expérience, c’est-à-dire sur des mesures pratiques. On définit l'exactitude d’une mesure en regardant l’écart entre cette mesure et la valeur théorique correcte de cette mesure.
Par exemple, disons que vous mesurez la longueur d’une table. Le fabricant de la table indique qu’elle mesure \(2.0\,m\) de long. Vous mesurez la longueur de la table trois fois, avec une règle graduée en \(cm\), et obtenez les mesures suivantes: \(2.01\,m\) \(1.99\,m\) et \(2.02\,m\). Ces mesures sont assez exactes car elles sont très proches de la valeur correcte de \(2\,m\). En revanche, si vous aviez obtenu une mesure de \(1.70\,m\), votre mesure ne serait pas très exacte.
Précision#
La précision d’un système de mesure se réfère à la proximité des mesures répétées (qui sont répétées dans les mêmes conditions). Considérez l’exemple des mesures de la table. La précision des mesures se réfère à l’écart des valeurs mesurées. Une manière d’analyser la précision des mesures serait de déterminer la différence entre la valeur mesurée la plus basse et la valeur mesurée la plus haute. Dans notre exemple, la valeur la plus basse était de \(1.99\,m\) et la valeur la plus haute était de \(2.02\,m\). Ainsi, les valeurs mesurées s’écartaient les unes des autres au maximum de \(0.03\,m=3\,cm\). Ces mesures étaient relativement précises car elles ne variaient pas trop en valeur. Cependant, si les valeurs mesurées avaient été de \(1.99\), \(2.01\) et \(2.42\), alors les mesures n’auraient pas été très précises car il y aurait eu une variation significative d’une mesure à l’autre.
Les mesures dans l’exemple de la table sont à la fois exactes et précises, mais dans certains cas, les mesures sont exactes mais pas précises, ou elles sont précises mais pas exactes. Considérons l’exemple d’un système GPS qui tente de localiser la position d’un restaurant dans une ville. Pensez à l’emplacement du restaurant comme existant au centre d’une cible, et pensez à chaque tentative du GPS de localiser le restaurant comme un point noir. Dans la figure 1.2a, vous pouvez voir que les mesures GPS sont éparpillées loin les unes des autres, mais elles sont centrées près de l’emplacement réel du restaurant au centre de la cible. Cela indique un système de mesure à faible précision, mais à haute exactitude. Cependant, dans la figure 1.2b, les mesures GPS sont concentrées assez près les unes des autres, mais elles sont loin de l’emplacement ciblé. Cela indique un système de mesure à haute précision, mais à faible exactitude.
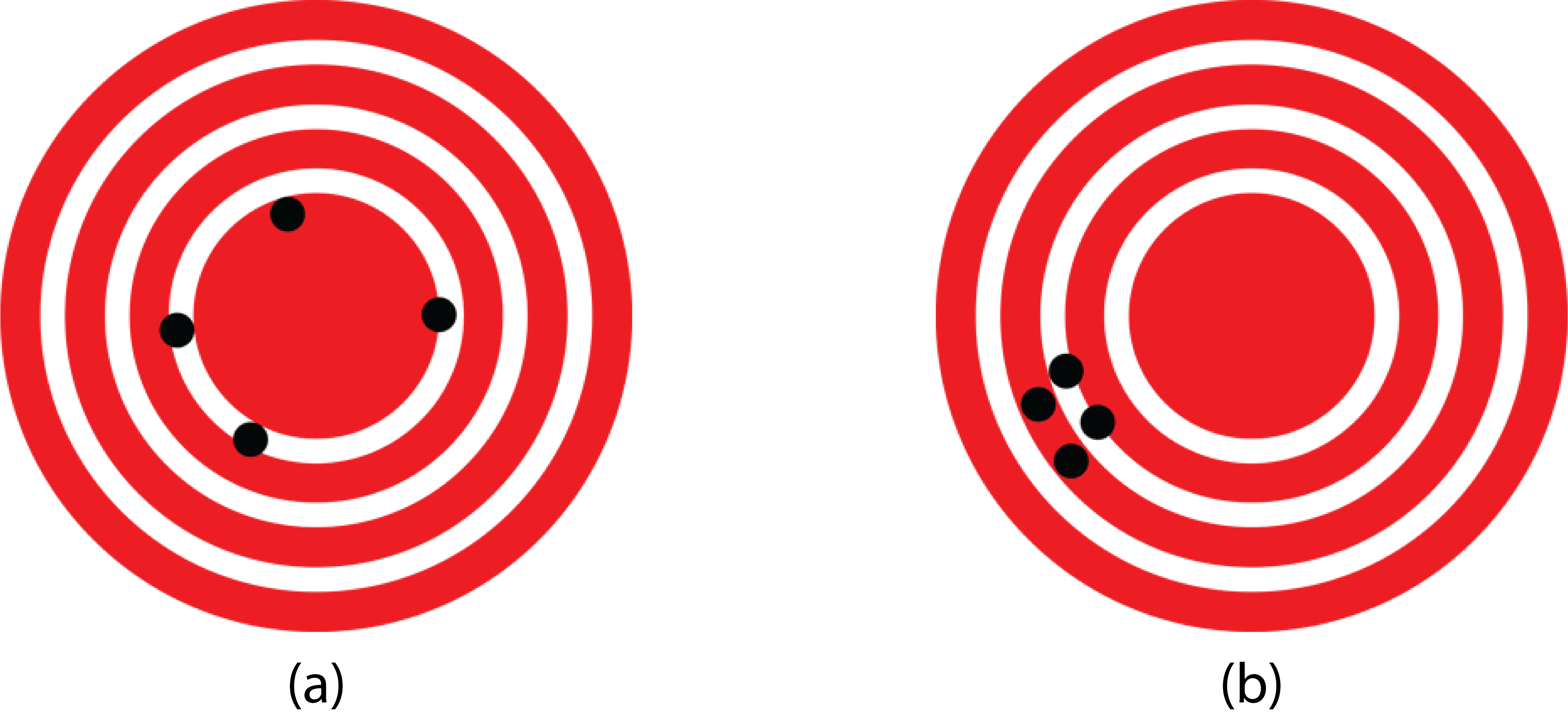
Fig. 1.2 (a) Un système GPS tente de localiser un restaurant au centre de la cible. Les points noirs représentent chaque tentative de préciser l’emplacement du restaurant. Les points sont assez éloignés les uns des autres, indiquant une faible précision, mais ils sont chacun plutôt proches de l’emplacement réel du restaurant, indiquant une haute exactitude. (b) Dans cette figure, les points sont concentrés assez près les uns des autres, indiquant une haute précision, mais ils sont assez loin de l’emplacement réel du restaurant, indiquant une faible exactitude. (crédit : Dark Evil)#
Incertitude absolue#
Le degré de précision et d’exactitude d’un système de mesure est lié à l'incertitude des mesures. L’incertitude (ou l'incertitude absolue) est une mesure de l’écart des valeurs mesurées par rapport à une valeur standard ou attendue (théorique). Si vos mesures ne sont pas très précises ou pas exactes, alors l’incertitude de vos valeurs sera très élevée. En termes plus généraux, l’incertitude peut être considérée comme une clause de non-responsabilité pour vos valeurs mesurées. Par exemple, si quelqu’un vous demandait de fournir le kilométrage de votre voiture, vous pourriez dire qu’il est de \(45'000\,km\), plus ou moins \(500\,km\). Le montant plus ou moins est l’incertitude de votre valeur. C’est-à-dire que vous indiquez que le kilométrage réel de votre voiture pourrait être aussi bas que \(44'500\,km\) ou aussi élevé que \(45'500\,km\), ou n’importe où entre les deux. Toutes les mesures contiennent une certaine quantité d’incertitude. Dans notre exemple de mesure de la longueur de la table, nous pourrions dire que la longueur de la table est de \(2.00\,m\), plus ou moins \(0.03\,m\).
Incertitude absolue
L’incertitude absolue d’une mesure \(A\), notée \(\Delta A\) (“delta A”), donne une information sur la précision du résultat de la mesure. La mesure sera alors notée comme :
Dans notre exemple de la table, la longueur de la table pourrait être exprimée comme \(2.00\pm 0.03\,m\)
Les facteurs contribuant à l’incertitude dans une mesure incluent :
Les limitations de l’appareil de mesure,
La compétence de la personne effectuant la mesure,
Les irrégularités dans l’objet mesuré,
Tout autre facteur qui affecte le résultat (fortement dépendant de la situation).
Dans notre exemple, les facteurs contribuant à l’incertitude pourraient être les suivants : la plus petite division sur la règle est le centimètre, donc \(0.01\,m\), On devrait donc théoriquement mesurer la longueur de la table comme \(2.00\pm 0.01\,m\). Notre incertitude plus grande peut provenir d’autres facteurs : la personne utilisant la règle a une mauvaise vue, ou un côté de la table est légèrement plus long que l’autre. En tout état de cause, l’incertitude dans une mesure doit être basée sur une considération attentive de tous les facteurs qui pourraient contribuer et de leurs effets possibles.
Connexions au monde réel - Fièvres ou Frissons ?
L’incertitude est une information cruciale, tant en physique que dans de nombreuses autres applications du monde réel. Imaginez que vous vous occupez d’un enfant malade. Vous suspectez que l’enfant a de la fièvre, alors vous vérifiez sa température avec un thermomètre. Et si l’incertitude du thermomètre était de \(3.0°C\) ? Si la lecture de la température de l’enfant était de \(37.0°C\) (qui est la température corporelle normale), la vraie température pourrait être n’importe où d’une hypothermie à \(34.0°C\) à une température dangereusement élevée de \(40.0°C\). Un thermomètre avec une incertitude de \(3.0°C\) serait inutile !
Incertitude relative#
Une méthode pour exprimer l’incertitude est en pourcentage de la valeur mesurée. C’est ce qu’on appelle l'incertitude relative.
Incertitude relative
Si une mesure \(A\) est exprimée avec une incertitude absolue \(\Delta A\), comme \(A\pm\Delta A\), alors l’incertitude relative \(\Delta A_{\,\%}\) (en pourcent) est définie comme :
L’incertitude relative permet de mieux quantifier notre précision de mesure.
Pour la même incertitude absolue (par exemple \(\pm 1\)), deux mesures peuvent avoir des incertitudes relatives, et donc des précisions, bien différentes.
Par exemple, \(300\pm 1\) a une incertitude relative de \(1\div 300=0.0033=0.33\,\%\) alors que \(3\pm 1\) a une incertitude relative de \(1\div 3=0.33=33\,\%\). On se rend ainsi bien compte de l’imprécision de la deuxième mesure.
Pour plus d’informations
Quelques liens utiles sur le même sujet :
autre lien à mettre
Incertitudes dans les calculs#
Il y a une incertitude dans tout ce qui est calculé à partir de quantités mesurées. Par exemple, la surface d’un sol calculée à partir des mesures de sa longueur et de sa largeur comporte une incertitude car la longueur et la largeur ont des incertitudes.
Quelle est l’ampleur de l’incertitude dans quelque chose que vous calculez par multiplication ou division ?
Si les mesures entrant dans le calcul ont de petites incertitudes (quelques pourcents ou moins), alors la méthode d’addition des pourcentages peut être utilisée pour la multiplication ou la division. Cette méthode indique que l’incertitude en pourcentage dans une quantité calculée par multiplication ou division est la somme des incertitudes en pourcentage dans les éléments utilisés pour faire le calcul
Par exemple, si un sol a une longueur de \(4.00\,m\) et une largeur de \(3.00\,m\), avec des incertitudes de \(2\,\%\) et \(1\,\%\), respectivement, alors la surface du sol est de \(12.0\,m^{2}\) et a une incertitude de \(3\,\%\). Exprimée en tant que surface, cela fait \(0.36\,m^{2}\), que nous arrondissons à \(0.4\,m^{2}\) (puisque la surface du sol est donnée à un dixième de mètre carré). La surface du est donc de \(12.0\pm 0.4\,m^{2}\).
Un rappel sur la base des calculs avec des incertitude se trouve dans la partie Rappels mathématiques au début de ce livre.
Précision des outils de mesure#
Un facteur important dans la précision et l’exactitude des mesures implique la précision de l’outil de mesure. En général, un outil de mesure précis est celui qui peut mesurer des valeurs en très petits incréments.
Par exemple, une règle standard peut mesurer la longueur au millimètre le plus proche, tandis qu’un pied à coulisse peut mesurer la longueur au centième de millimètre le plus proche. Le pied à coulisse est un outil de mesure plus précis parce qu’il peut mesurer des différences de longueur extrêmement petites. Plus l’outil de mesure est précis, plus les mesures peuvent être précises et exactes.
Lorsque nous exprimons des valeurs mesurées, nous ne pouvons lister que le nombre de chiffres que nous avons initialement mesurés avec notre outil de mesure. Par exemple, si vous utilisez une règle standard pour mesurer la longueur d’un bâton, vous pouvez le mesurer à \(36.7\,cm\). Vous ne pourriez pas exprimer cette valeur comme \(36.71\,cm\) parce que votre outil de mesure n’était pas assez précis pour mesurer un centième de centimètre.
Il faut noter que le dernier chiffre dans une valeur mesurée a été estimé d’une certaine manière par la personne effectuant la mesure. Par exemple, la personne mesurant la longueur d’un bâton avec une règle remarque que la longueur du bâton semble être quelque part entre \(36.6\,cm\) et \(36.7\,cm\), et elle doit estimer la valeur du dernier chiffre. En utilisant la méthode des chiffres significatifs, la règle est que le dernier chiffre écrit dans une mesure est présenté avec une certaine incertitude. Pour déterminer le nombre de chiffres significatifs dans une valeur, commencez avec la première valeur mesurée à gauche et comptez le nombre de chiffres jusqu’au dernier chiffre écrit à droite. Par exemple, la valeur mesurée \(36.7\,cm\) a trois chiffres significatifs. Les chiffres significatifs indiquent la précision d’un outil de mesure qui a été utilisé pour mesurer une valeur.
Zéros#
Une considération spéciale est donnée aux zéros lors du comptage des chiffres significatifs. Comme on l’a vu dans la partie sur les Chiffres significatifs, les zéros dans \(0.053\) ne sont pas significatifs, car ils ne sont que des gardiens de place qui localisent le point décimal. Il n’y a que deux chiffres significatifs dans \(0.053\).
Les zéros dans \(10.053\) ne sont pas des gardiens de place mais sont des chiffres significatifs. \(10.053\) a cinq chiffres significatifs.
Les zéros dans \(1300\) peuvent ou non être significatifs selon le style d’écriture des nombres. Ils pourraient signifier que le nombre est connu jusqu’au dernier chiffre, ou ils pourraient être des gardiens de place. Ainsi, \(1300\) pourrait avoir deux, trois ou quatre chiffres significatifs. Pour éviter cette ambiguïté, on écrira de préférence, \(1300\) en notation scientifique : \(1.3\cdot 10^{3}\), \(1.30\cdot 10^{3}\) ou \(1.300\cdot 10^{3}\). La notation utilisée indiquera alors le nombre de chiffre significatif à retenir. Si on veut par exemple trois chiffres significatif, alors on écrira \(1300\) comme \(1.30\cdot 10^3\).
Les zéros sont significatifs sauf lorsqu’ils servent uniquement de gardiens de place.
YouTube
Quelques liens de vidéo utiles sur le même sujet :
Calculs des incertitudes au lycée
