Manipuler les équations#
Remonter vers l’inconnue#
Opérations réversibles#
Les équations les plus simples à résoudre sont celles dans lesquelles l’inconnue ne subit que des transformations facilement réversibles. Pour comprendre ce que cela signifie, regardons l’équation suivante :
En algèbre rhétorique la même équation donnerait ceci : quel nombre donne \(16\) si on lui ajoute \(5\) ? Un peu de réflexion, permet de trouver la solution sans trop de problème : \(x=11\), en effet, \(11+5=16\).
Si cette équation est simple à résoudre, c’est parce que l’inconnue ne subit qu’une seule opération : une addition. Or l’addition est une opération qui permet de revenir en arrière facilement : il suffit de faire une soustraction. Pour trouver la solution, on a simplement fait \(16-5=11\), car la soustraction est l’opération inverse de l’addition.
Astuce
En fait, les quatre opérations de base sont facilement réversibles :
une addition s’inverse avec une soustraction ;
une soustraction s’inverse avec une addition ;
une multiplication s’inverse avec une division ;
une division s’inverse avec une multiplication.
Par conséquent, si dans une équation, l’inconnue ne subit que ces quatre opérations de base, alors la solution est facile à trouver.
Regardons par exemple l’équation suivante :
L’inconnue \(x\) subit successivement chacune des quatre opérations pour aboutir à \(10\). Cette équation peut se représenter par le schéma suivant :

Pour résoudre cette équation, il suffit alors de refaire le chemin à l’envers en partant du 10 et en inversant chacune des opérations.
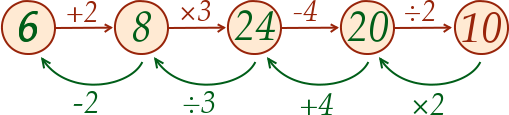
Et voilà le travail ! L’équation est résolue : la solution est \(x=6\). Si vous n’y croyez pas, remplacez le \(x\) par \(6\) dans l’équation de départ et vous verrez que ça marche :
Complications#
Les puissances#
Tant que l’on a que les quatre opérations de base dans notre équation, tout se passe donc plutôt bien. Les choses commencent à se compliquer dès que les puissances apparaissent. Le problème avec les puissance c’est qu’elles ne sont pas réversibles de façon unique. Regardons par exemple l’équation suivante :
Cette équation peut se représenter de la façon suivante :
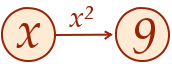
Quand les \(x\) sont plusieurs#
Là où ça se complique vraiment, c’est quand les \(x\) commencent à être plusieurs dans l’équation. Prenons par exemple l’équation suivante :
Cette fois, la méthode précédente ne marche pas. En effet, l’inconnue \(x\) apparaît deux fois, ce qui rend impossible la remontée vers l’inconnue en appliquant simplement des opérations inverses.
Astuce
Si vous vous creusez un peu la tête peut-être arriverez vous à trouver les solutions de l’équation ci-dessus. Il y en a deux : 1 et -2. Cependant, ce qui nous importe, ce n’est pas d’avoir les solutions de cette équation en particulier mais plutôt des méthodes pour pouvoir résoudre de façon systématique les équations de ce type. Ici, les solutions sont des nombres entiers donc on peut les deviner en cherchant un peu mais s’il s’agissait de nombres plus compliqués il deviendrait impossible de les débusquer uniquement en observant l’équation.
Ce genre d’équation est beaucoup plus subtile et demande l’utilisation de techniques plus avancées. Mais même ces techniques ne marchent pas à tous les coups : il existe certaines équations pour lesquelles même les mathématiciens d’aujourd’hui ne connaissent pas de méthode générale pour calculer les solutions !
Transformons les équations#
La règle fondamentale de manipulation des équations#
La règle fondamentale de manipulation des équations est la suivante :
Astuce
On ne change pas les solutions d’une équation en appliquant la même transformation réversible à ses deux termes.
Prenons encore une fois l’exemple des quatre opérations de base, dont nous avons déjà vu qu’elles étaient réversibles. Alors, si on a une équation, on peut lui ajouter, lui soustraire, la multiplier ou la diviser par un nombre quelconque.
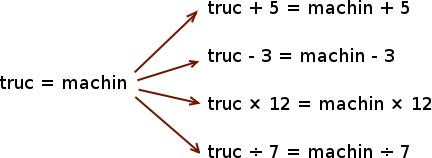
Astuce
Attention à une petite exception, vous savez qu’il est impossible de diviser par zéro. Par conséquent, il n’est pas possible de diviser une équation par \(0\) et cela entraîne également que la multiplication par \(0\) n’est pas réversible.
Pour illustrer l’utilité de cette règle, reprenons l’exemple de la première équation que nous avons vue au début de ce chapitre :
Alors, il est possible de faire l’opération \(-5\) de chaque côté de l’équation, on obtient alors :
Les \(+5-5\) s’annulent à gauche, ce qui donne au final :
Cette manipulation nous a permis d’isoler le \(x\) et donc de résoudre l’équation. Bon, dans ce cas, ce n’est pas révolutionnaire comme méthode vu que la solution est vraiment simple à trouver et que nous la connaissions déjà, mais nous allons voir par la suite que sur des équations plus compliquées, cela permet de simplifier beaucoup de choses.
Quand les termes changent de côté#
Ce genre de transformation permet de faire changer de côté certains termes des équations. Imaginons que l’on a une équation de la forme suivante :
Et supposons que pour résoudre l’équation, il soit préférable que truc se trouve de l’autre côté de l’égalité. Alors il est possible de le soustraire des deux côtés et on obtient ceci :
On voit alors que les trucs s’annulent dans le terme de gauche, on obtient donc ceci :
Remarquez cette chose amusante : en passant de l’autre côté, le signe du truc a changé, c’était un \(+\) et c’est devenu un \(-\).
La règle, est donc la suivante : quand un terme est additionné ou soustrait d’un côté d’une équation, on peut le faire passer de l’autre côté en changeant son signe. Autrement dit, en passant de l’autre côté du signe =, les additions se transforment en soustraction et inversement.
Notez l’utilisation du symbole \(\Leftrightarrow\) dans la résolution ci-dessus. Il s’agit du symbole d’équivalence qui signifie ici que les deux équations peuvent se déduire l’une de l’autre.
La même chose est vraie pour la multiplication et la division.
Astuce
Dans ce cas là, il faut toutefois vérifier avant de faire la transformation que truc n’est pas égal à \(0\) car la division par \(0\) est impossible.
Pour plus d’informations
Quelques liens utiles sur le même sujet :
2e LIENS A METTRE!!!
YouTube
Quelques liens de vidéo utiles sur le même sujet :
Manipulation de formule littérale - niveau 1 | Physique - chimie | Collège - Lycée
Manipulation de formule littérale - niveau 2 | Physique - Chimie | Collège - Lycée
Comment transformer une formule en physique - méthode en 5 minutes
Comment manipuler une formule de physique avec division ?

Comment faire alors pour revenir à \(x\) en connaissant \(x^2\) ?#
Spontanément, on a envie de répondre que la réponse se trouve grâce à la racine carrée. En effet, \(\sqrt{9}=3\) est bien solution à notre équation : si on remplace \(x\) par 3, on a bien \(3^{2}=9\).
Seulement voilà, en faisant ça, on a oublié une solution : \(-3\). En effet, on a également \((-3)^{2}=9\). Un nombre strictement positif possède toujours deux racines carrées et le symbole \(\sqrt{}\) sert à désigner celle des deux qui est positive.
Le carré nous permet donc de découvrir une nouvelle facette des équations : une équation peut avoir plusieurs solutions. En l’occurrence, l’équation \(x^2=9\) possède deux solutions, \(-3\) et \(3\). Cela peut se représenter de la façon suivante :
Une fois que l’on a compris cela, on peut trouver des équations avec de multiples solutions en ajoutant des carrés. Regardons par exemple l’équation suivante :
On peut la représenter comme ceci :
Puis, le schéma suivant permet de trouver ses solutions :
Il y a deux carrés dans l’équation, les solutions se dédoublent donc deux fois. Ainsi, l’équation possède quatre solutions : \(-4\), \(-2\), \(2\) et \(4\).
En multipliant le nombre de carrés dans l’équation, on multiplie à chaque fois le nombre de solutions. Avec ce procédé, vous pouvez donc imaginer des équations ayant autant de solutions que vous voulez.