8.1. Mouvement Rectiligne à 2 Dimensions

Décomposition du mouvement

L’arc d’un ballon de basket, l’orbite d’un satellite, un vélo contournant une courbe, un nageur plongeant dans une piscine, du sang jaillissant d’une blessure et un chiot poursuivant sa queue ne sont que quelques exemples de mouvements le long de trajectoires courbes. En fait, la plupart des mouvements dans la nature suivent des trajectoires courbes plutôt que des lignes droites. Le mouvement le long d’une trajectoire courbe sur une surface plane ou un plan (comme celui d’une balle sur une table de billard ou d’un patineur sur une patinoire) est bidimensionnel, et donc décrit par une cinématique bidimensionnelle. Un mouvement non confiné à un avion, comme une voiture suivant une route de montagne sinueuse, est décrit par une cinématique tridimensionnelle. Les cinématiques bidimensionnelles et tridimensionnelles sont de simples extensions de la cinématique unidimensionnelle développée pour le mouvement en ligne droite dans les chapitres précédents. Cette simple extension nous permettra d’appliquer la physique à beaucoup plus de situations.

\section{Mouvement bidimensionnel: Marcher dans une ville} Supposons que vous vouliez marcher d’un point à un autre dans une ville avec des blocs carrés uniformes, comme illustré à la Fig. 8.1.

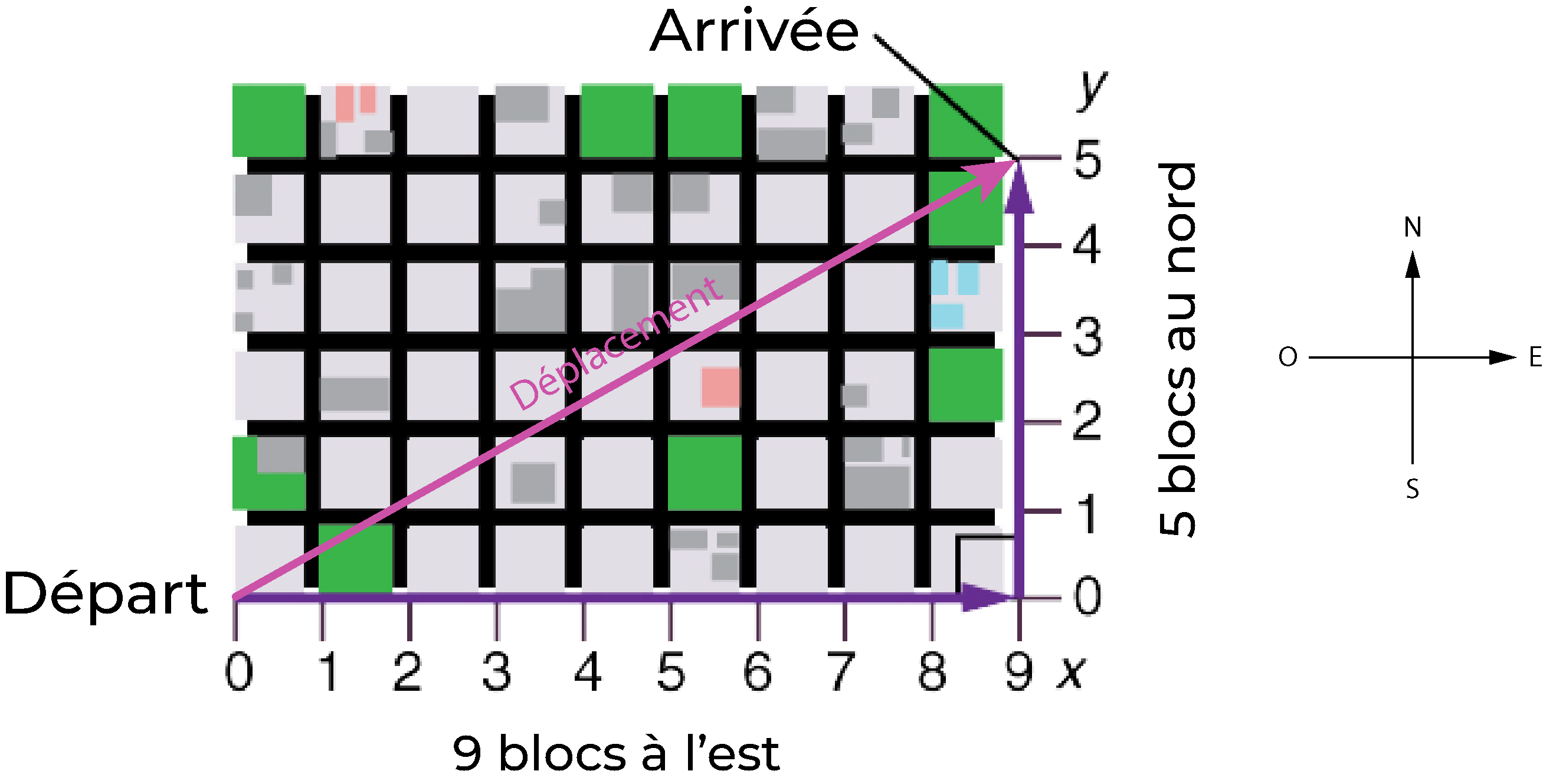
Fig. 8.1 Un piéton parcourt un chemin bidimensionnel entre deux points d’une ville. Dans cette scène, tous les blocs sont carrés et ont la même taille. (crédit : openstax.org)

Le chemin en ligne droite qu’un hélicoptère pourrait suivre vous est bloqué en tant que piéton, et vous êtes donc obligé d’emprunter un chemin en deux dimensions, tel que celui illustré. Vous parcourez donc \(14\) pâtés de maisons en tout, \(9\) à l’est suivis de \(5\) au nord. Mais quelle est la distance en ligne droite ?

Les deux chemin parcourus par le piéton et le chemin en ligne droite utilisé par l’hélicoptère forment un triangle rectangle, et donc le théorème de Pythagore, \(a^{2}+b^{2}=c^{2}\), peut être utilisé pour trouver la distance en ligne droite. la Fig. 8.1.

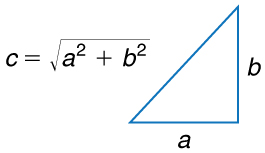
Fig. 8.2 Le théorème de Pythagore relie la longueur des côtés de l’angle droit d’un triangle rectangle, notés \(a\) et \(b\), avec l’hypoténuse, notée \(c\). La relation est donnée par : \(a^{2} + b^{2} = c^{2}\). Ceci peut être réécrit en résolvant pour \(c\) : \(c=\sqrt{a^{2} + b^{2}}\). (crédit : openstax.org)

L’hypoténuse du triangle est le chemin en ligne droite, et donc dans ce cas, sa longueur en unités de pâtés de maisons est \(\sqrt{(9\,blocs)^{2} + (5\,blocs)^{2}}=10.3\,blocs\), considérablement plus court que les \(14\) blocs que vous avez parcourus.

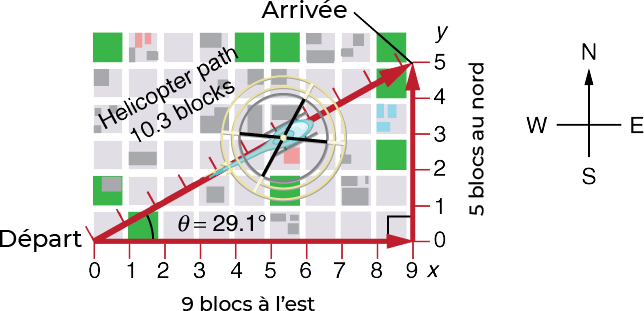
Fig. 8.3 Le trajet en ligne droite suivi par un hélicoptère entre les deux points est plus court que les 14 blocs parcourus par le piéton. Tous les blocs sont carrés et de la même taille. (crédit : openstax.org)

Le trajet en ligne droite suivi par un hélicoptère entre les deux points est plus court que les \(14\) blocs parcourus par le piéton. Tous les blocs sont carrés et de la même taille. Le fait que la distance en ligne droite (\(10.3\) blocs) de la Fig. 8.3 soit inférieure à la distance totale parcourue (\(14\) blocs) est un exemple d’une caractéristique générale des vecteurs. (Rappelez-vous que les vecteurs sont des quantités qui ont à la fois une amplitude et une direction.)

Comme pour la cinématique unidimensionnelle, nous utilisons des flèches pour représenter les vecteurs. La longueur de la flèche est proportionnelle à la magnitude du vecteur. La longueur de la flèche est indiquée par des traits dièses dans la figure Fig. 8.1 et la Fig. 8.3. La flèche pointe dans la même direction que le vecteur. Pour un mouvement bidimensionnel, la trajectoire d’un objet peut être représentée par trois vecteurs: un vecteur montre la trajectoire en ligne droite entre les points initial et final du mouvement, un vecteur montre la composante horizontale du mouvement et un vecteur montre la composante verticale du mouvement. Les composantes horizontale et verticale du mouvement s’additionnent pour donner la trajectoire en ligne droite. Par exemple, observez les trois vecteurs de la Fig. 8.3. Le premier représente un déplacement de \(9\) blocs vers l’est. La seconde représente un déplacement de \(5\) blocs vers le nord. Ces vecteurs sont ajoutés pour donner le troisième vecteur, avec un déplacement total de \(10.3\) blocs. Le troisième vecteur est le chemin en ligne droite entre les deux points. Notez que dans cet exemple, les vecteurs que nous ajoutons sont perpendiculaires les uns aux autres et forment ainsi un triangle rectangle. Cela signifie que nous pouvons utiliser le théorème de Pythagore pour calculer l’amplitude du déplacement total. (Notez que nous ne pouvons pas utiliser le théorème de Pythagore pour ajouter des vecteurs qui ne sont pas perpendiculaires.)

Indépendance des mouvements perpendiculaires

La personne qui emprunte le chemin illustré à la Fig. 8.3 marche vers l’est puis vers le nord (deux directions perpendiculaires). La distance à laquelle ils marchent vers l’est n’est affectée que par leur mouvement vers l’est. De même, la distance à laquelle ils marchent vers le nord n’est affectée que par leur mouvement vers le nord.

Indépendance du mouvement

Les composantes horizontale et verticale du mouvement bidimensionnel sont indépendantes l’une de l’autre. Tout mouvement dans le sens horizontal n’affecte pas le mouvement dans le sens vertical, et vice versa.

Cela est vrai dans un scénario simple comme celui de marcher d’abord dans une direction, suivie d’une autre. C’est également vrai pour les mouvements plus compliqués impliquant un mouvement dans deux directions à la fois. Par exemple, comparons les mouvements de deux balles de baseball. Une balle de baseball est lâchée d’une certaine hauteur. Au même instant, l’autre est lancée horizontalement de la même hauteur et suit une trajectoire courbe. Un stroboscope a capturé les positions des balles à des intervalles de temps fixes lors de leur chute.

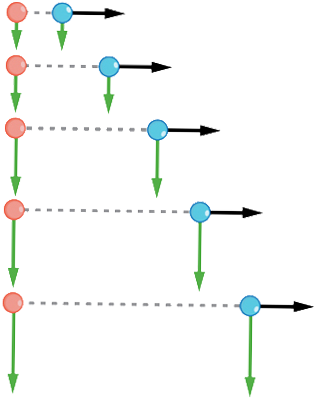
Fig. 8.4 Ceci montre les mouvements de deux balles identiques - l’une tombe du repos, l’autre a une vitesse horizontale initiale. Chaque position suivante est un intervalle de temps égal. Les flèches représentent les vitesses horizontales et verticales à chaque position. La boule de droite a une vitesse horizontale initiale, tandis que la boule de gauche n’a pas de vitesse horizontale. Malgré la différence des vitesses horizontales, les vitesses verticales et les positions sont identiques pour les deux balles. Cela montre que les mouvements verticaux et horizontaux sont indépendants. (crédit : openstax.org)

Il est remarquable que pour chaque instant, les positions verticales des deux boules soient les mêmes. Cette similitude implique que le mouvement vertical est indépendant du fait que la balle se déplace horizontalement ou non. (En supposant qu’il n’y ait pas de résistance de l’air, le mouvement vertical d’un objet qui tombe n’est influencé que par la gravité et non par des forces horizontales.) Un examen attentif de la balle lancée horizontalement montre qu’elle parcourt la même distance horizontale entre les flash du stroboscope. Cela est dû au fait qu’il n’y a pas de forces supplémentaires sur la balle dans la direction horizontale après son lancement. Ce résultat signifie que la vitesse horizontale est constante et n’est affectée ni par le mouvement vertical ni par la gravité (qui est verticale). Notez que ce cas n’est vrai que pour des conditions idéales. Dans le monde réel, la résistance de l’air modifiera la vitesse de la balle dans les deux directions.

La trajectoire courbe bidimensionnelle de la balle lancée horizontalement est composée de deux mouvements unidimensionnels indépendants (horizontal et vertical). La clé pour analyser un tel mouvement est de le résoudre (décomposer) en deux mouvements le long des directions perpendiculaires. La décomposition du mouvement bidimensionnel en deux mouvements perpendiculaires est possible car les composantes sont indépendantes.

Le mouvement de projectile est le mouvement d’un objet lancé ou projeté dans l’air, soumis uniquement à l’accélération de la gravité. L’objet est appelé un projectile, et son chemin est appelé sa trajectoire. Le mouvement des objets en chute libre, tel que décrit dans la leçon sur La chute libre, est un type simple de mouvement unidimensionnel d’objets dans lequel il n’y a pas de mouvement horizontal. Dans cette leçon, nous considérons le mouvement bidimensionnel d’un objet, comme celui d’un ballon de football ou d’un autre objet pour lequel la résistance de l’air est négligeable.

Le fait le plus important à retenir ici est que les mouvements le long des axes perpendiculaires sont indépendants et peuvent donc être analysés séparément. La clé est que pour analyser le mouvement bidimensionnel d'un objet, il faut le décomposer en deux mouvements rectilignes, l'un le long de l'axe horizontal et l'autre le long de l'axe vertical. Ce choix d’axes est judicieux ici, car l’accélération due à la gravité est verticale - ainsi, il n’y aura pas d’accélération le long de l’axe horizontal lorsque la résistance de l’air est négligeable.

Comme il est d’usage, nous appelons l’axe horizontal l’axe des \(x\) et l’axe vertical l’axe \(y\). La Fig. 8.5 illustre la notation du déplacement, où \(\vec{r}\) est défini comme étant le déplacement total et \(\vec{x}\) et \(\vec{y}\) sont ses composantes le long de l’axe horizontal et vertical, respectivement. Les grandeurs de ces vecteurs sont \(r\), \(x\) et \(y\).

Notez que dans la dernière section, nous avons utilisé la notation \(\vec{A}\) pour représenter un vecteur avec ses composantes \(\vec{A}_{x}\) et \(\vec{A}_{y}\). Si on continuait ce format, on appellerait déplacement \(\vec{r}\) avec des composants \(\vec{r}_{x}\) et \(\vec{r}_{y}\). Cependant, pour simplifier la notation, nous allons simplement représenter les composantes des vecteurs par \(\vec{x}\) et \(\vec{y}\).

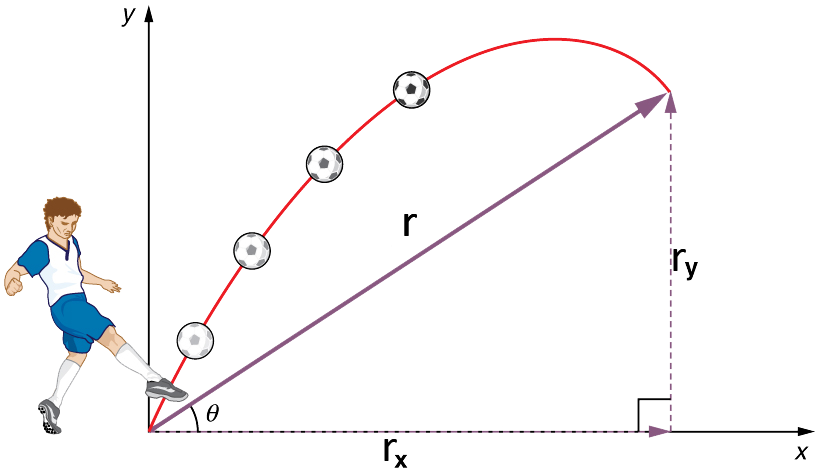
Fig. 8.5 Le déplacement total \(r\) d’un ballon de football en un point de sa trajectoire. Le vecteur \(\vec{r}\) a comme composantes \(\vec{r}_{x}\) et \(\vec{r}_{y}\) (notées \(\vec{x}\) et \(\vec{y}\) par la suite) selon l’axe horizontal et vertical. Son amplitude est \(r\), et il fait un angle \(\theta\) avec l’horizontale. (crédit : openstax.org)

YouTube

Quelques liens de vidéo utiles sur le même sujet :

1. Qu’est-ce qu’une chronophotographie ?

2. Chronophotographie d’un mouvement

Résolution des problèmes de cinématique à deux dimensions

Pour décrire le mouvement, nous devons traiter de la vitesse et de l’accélération, ainsi que du déplacement. Nous devons également trouver leurs composants le long des axes \(x\) et \(y\). Nous supposerons que toutes les forces à l’exception de la gravité (telles que la résistance de l’air et le frottement, par exemple) sont négligeables. Les composantes de l’accélération sont alors très simples: \(a_{y}=-g=-9,81 m/s^{2}\). Notez que cette définition suppose que la direction vers le haut est définie comme la direction positive. Si vous organisez le système de coordonnées à la place de sorte que la direction vers le bas soit positive, l’accélération due à la gravité prend une valeur positive. Comme la gravité est verticale, \(a_{x}=0\). Les deux accélérations sont constantes, de sorte que les équations cinématiques peuvent être utilisées.

Étapes de résolution des problèmes à deux dimensions

Compte tenu de ces hypothèses, les étapes suivantes sont ensuite utilisées pour analyser le mouvement du projectile :

Étape 1

Résolvez ou décomposez le mouvement en composants horizontaux et verticaux le long des axes \(x\) et \(y\). Comme ces axes sont perpendiculaires, la valeur des composantes (l’amplitude) de n’importe quel vecteur \(\vec{A}\) peuvent se calculer avec \(A_{x}=A\cdot \cos\alpha\) et \(A_{y}=A\cdot \sin\alpha\). Les composantes du déplacement \(\vec{r}\) le long de ces axes sont \(x\) et \(y=\), et les composantes de la vitesse \(\vec{v}\) sont donc \(v_{x}=v\cdot \cos\theta_{v}\) et \(v_{y}=v\cdot \cos\theta_{v}\), où \(v\) est l’amplitude de la vitesse et \(\theta_{v}\) sa direction, comme le montre la Fig. 8.6 Les valeurs initiales sont notées avec un indice \(0\), comme d’habitude.

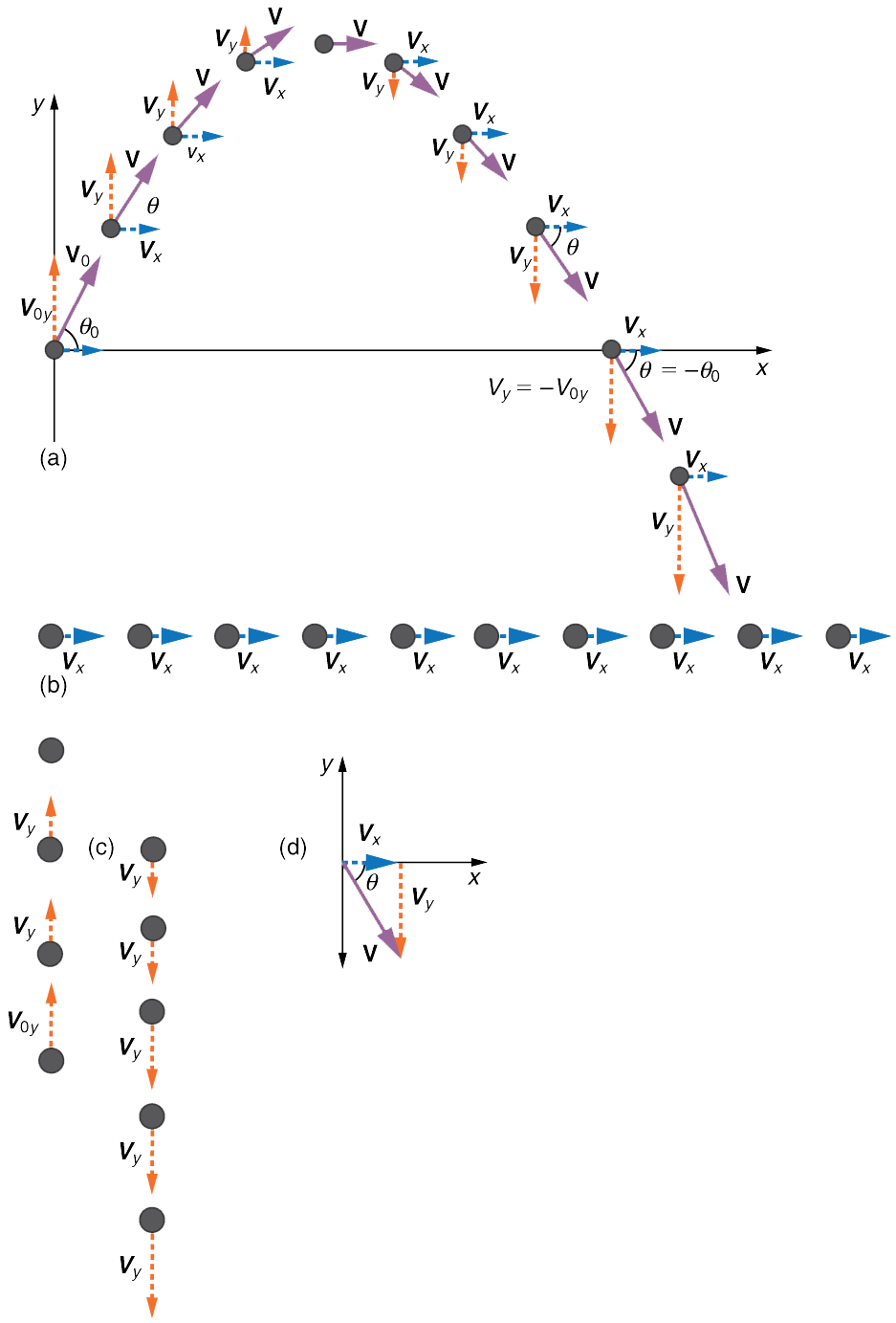
Fig. 8.6 (a) Nous analysons le mouvement bidimensionnel du projectile en le décomposant en deux mouvements unidimensionnels indépendants le long des axes vertical et horizontal. (b) Le mouvement horizontal est simple, car \(a_{x}=0\) et \(v_{x}\) est donc constant. (c) La vitesse dans la direction verticale commence à diminuer à mesure que l’objet s’élève; à son point le plus haut, la vitesse verticale est nulle. Lorsque l’objet retombe vers la Terre, la vitesse verticale augmente à nouveau en amplitude mais pointe dans la direction opposée à la vitesse verticale initiale. (d) Les mouvements \(x\) et \(y\) sont recombinés pour donner la vitesse totale en un point donné de la trajectoire. (crédit : openstax.org)

Étape 2

Traitez le mouvement comme deux mouvements unidimensionnels indépendants, l’un horizontal et l’autre vertical. Les équations cinématiques des mouvements horizontaux et verticaux prennent les formes suivantes :

Sur l’axe horizontal (\(x\))

\[\begin{split}\begin{align*} x(t) &=v_{0}t+x_{0}\\ v(t)_{x}&= v_{0x}=constante\\ a_{x}&= 0\\ \end{align*}\end{split}\]

Sur l’axe vertical (\(y\))

\[\begin{split}\begin{align*} y(t) &=-\dfrac{1}{2}gt^{2}+v_{0y}t+y_{0}\\ v(t)_{y }&=-gt+v_{0y}\\ y(t)-y_{0} &=\dfrac{1}{2}(v(t)+v_{0y}\cdot t\\ v(t)_{y}^{2}-v_{0y}^{2}&=-2g(y(t)-y_{0})\\ a_{y} &=-g=-9.81\,m/s^{2}\\ \end{align*}\end{split}\]

Étape 3

Trouvez les inconnues dans les deux mouvements distincts, un horizontal (\(x\)) et un vertical (\(y\)). Notez que la seule variable commune entre les mouvements sur \(\boldsymbol{x}\) et \(\boldsymbol{y}\), est le temps \(\boldsymbol{t}\). Les procédures de résolution de problèmes ici sont les mêmes que pour la cinématique unidimensionnelle et sont illustrées dans les exemples résolus ci-dessous.

Étape 4

Recombinez les deux mouvements pour trouver le déplacement total \(\vec{r}\) et la vitesse \(\vec{v}\). Étant donné que les mouvements sur \(x\) et \(y\) sont perpendiculaires, nous déterminons ces vecteurs en utilisant Pythagore et la trigonométrie.

\[\begin{split}\begin{align*} r(t) &= \sqrt{x(t)^{2}+y(t)^{2}}\\ \theta (t) &= \tan^{-1}\left(\dfrac{y(t)}{x(t)}\right)\\ \\ v(t) &= \sqrt{v_{x}(t)^{2}+v_{y}(t)^{2}}\\ \theta_{v}(t) &= \tan^{-1}\left(\dfrac{v_{y}(t)}{v_{x}(t)}\right) \end{align*}\end{split}\]

Exemple : Un feux d’artifice qui explose haut et loin

Lors d’un feu d’artifice, un obus est tiré en l’air à une vitesse initiale de \(70.0\,m/s\) sous un angle de \(75,0°\) au-dessus de l’horizontale, comme illustré ci-dessous. La mèche d’allumage est calibrée pour enflammer l’obus juste au moment où il atteint son point le plus élevé au-dessus du sol.

1. Calculez la hauteur à laquelle l’obus explose.

2. Combien de temps s’est-il écoulé entre le lancement de l’obus et l’explosion ?

3. Quel est le déplacement horizontal de l’obus lorsqu’il explose ?

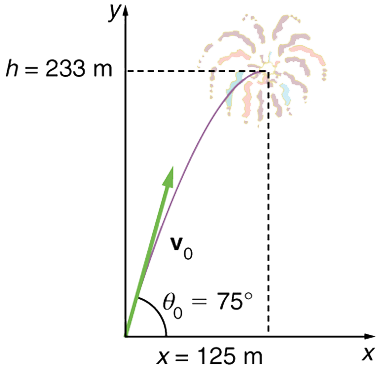
Fig. 8.7 Trajectoire d’un obus pyrotechnique. Le fusible est réglé pour faire exploser l’obus au point le plus haut de sa trajectoire, qui se trouve à une hauteur de \(233\,m\) et à \(125\,m\) de distance horizontalement. (crédit : openstax.org)

stratégie

Étant donné que la résistance de l’air est négligeable pour l’obus non explosé, la méthode d’analyse décrite ci-dessus peut être utilisée.
Le mouvement peut être décomposé en mouvements horizontaux et verticaux dans lesquels \(a_{x}=0\) et \(a_{y}=-g\).
On peut alors définir \(x_{0}\) et \(y_{0}\) à zéro et résoudre pour les quantités souhaitées.

solution

Pour simplifier la notation, nous écrirons \(y\), \(v_{x}\) et \(v_{y}\) au lieu de \(y(t)\), \(v_{x}(t)\) et \(v_{y}(t)\)

Solution 1.

Par hauteur, nous entendons la position verticale \(y\) au-dessus du point de départ (altitude du point). Le point le plus élevé de toute trajectoire, appelé sommet, est atteint lorsque \(v_{y}=0\). Puisque nous connaissons les vitesses initiale et finale ainsi que la position initiale, nous utilisons l’équation suivante pour trouver \(y\) :

\[v_{y}^{2}-v_{0y}^{2}=-2g(y-y_{0})\]

Comme \(y_{0}\) et \(v_{y}\) sont tous deux nuls à l’endroit considéré, l’équation se simplifie en

\[0=v_{0y}^{2}-2g\cdot y\]

et donc :

\[y=\dfrac{v_{0y}^{2}}{2g}\]

Il faut maintenant trouver \(v_{0y}\), la composante de la vitesse initiale dans la direction \(y\). Elle est donné par \(v_{0y}=v_{0}\sin\theta\), où \(v_{0}\) est la vitesse initiale de \(70.0\,m/s\), et \(\theta =75.0°\) est l’angle initial.
On obtient ainsi,

\[v_{0y}=v_{0}\sin\theta=70.0\,m/s\cdot\sin 75.0°=67.6\,m/s\]

Ce qui nous donne finalement :

\[y=\dfrac{(67.6\,m/s)^{2}}{2(9.81\,m/s^{2})^{2}}=233\,m\]

Solution 2.

Comme dans de nombreux problèmes de physique, il existe plusieurs façons de résoudre le temps jusqu’au point le plus élevé. Dans ce cas, une des méthodes consiste à utiliser \(v_{y}=v_{0y}-gt\). Comme \(v_{y}\) est nul, cette équation se réduit à :

\[v_{0y}=gt\]

et donc:

\[t=\dfrac{v_{0y}}{g}=\dfrac{67.6\,m/s}{9.81\,m/s^{2}}=6.89\,s\]

Solution 3.

Parce que la résistance de l’air est négligeable, \(a_{x}=0\) et la vitesse horizontale est constante, comme discuté ci-dessus. Le déplacement horizontal est la vitesse horizontale multipliée par le temps, donnée par \(x=x_{0}+v_{0x}t\), où \(x_{0}\) est égal à zéro :

\[x=v_{0x}t\]

où \(v_{0x}\) est la composante \(x\) de la vitesse, qui est donnée par \(v_{0x}=v_{x}\cos\theta\)

\[v_{0x}=v_{x}\cos\theta=(70\,m/s)\cos 75°=18.1\,m/s\]

Le temps \(t\) est le même pour les deux mouvements, on a ainsi :

\[x=(18.1\,m/s)(6.89\,s)=125\,m\]

discussion

Discussion 1.

Notez que parce que la direction vers le haut est positive, la vitesse initiale est positive, tout comme la hauteur maximale, mais l’accélération due à la gravité est négative. Notez également que la hauteur maximale ne dépend que de la composante verticale de la vitesse initiale, de sorte que tout projectile avec une composante verticale initiale de vitesse de \(67.6\,m/s\) atteindra une hauteur maximale de \(233\,m\) (en négligeant la résistance de l’air). Les chiffres de cet exemple sont raisonnables pour de grands feux d’artifice, dont les obus atteignent de telles hauteurs avant d’exploser. En pratique, la résistance de l’air n’est pas complètement négligeable, et il faudrait donc que la vitesse initiale soit un peu plus grande que celle donnée pour atteindre la même hauteur.

Discussion 2.

Ce temps est également raisonnable pour les grands feux d’artifice. Lorsque vous pourrez voir le lancement d’un feu d’artifice, vous remarquerez que plusieurs secondes s’écoulent avant que l’obus n’explose.

Une autre façon de trouver le temps est d’utiliser \(y=y_{0}+v_{0y}t-\dfrac{1}{2}gt^{2}\), et de résoudre l’équation du \(2^{e}\) degré pour t. Il est aussi possible de résoudre cet exercice en utilisant la vitesse moyenne \(v_{moy}=\dfrac{y-y_{0}}{t}=\dfrac{v_{y}+v_{0y}}{2}\).

Discussion 3.

Le mouvement horizontal se fait à une vitesse constante en l’absence de résistance de l’air. Le déplacement horizontal trouvé ici pourrait être utile pour empêcher les fragments de feux d’artifice de tomber sur les spectateurs. Une fois que l’obus explose, la résistance de l’air a un effet majeur et de nombreux fragments atterriront directement en dessous.

En résolvant la partie (a) de l’exemple précédent, l’expression que nous avons trouvée pour \(y\) est valable pour tout mouvement de projectile où la résistance de l’air est négligeable. Appelez la hauteur maximale \(y=h\); alors,

\[h=\dfrac{v_{0y}^{2}}{2g}\]

Cette équation définit la hauteur maximale d’un projectile et ne dépend que de la composante verticale de la vitesse initiale.

Définition d’un système de coordonnées

Il est important de mettre en place un système de coordonnées lors de l’analyse du mouvement du projectile. Une partie de la définition du système de coordonnées consiste à définir une origine pour les positions \(x\) et \(y\). Souvent, il est commode de choisir la position initiale de l’objet comme origine de sorte que \(x_{0}=0\) et \(y_{0}=0\).

Il est également important de définir les directions positives et négatives dans les directions \(x\) et \(y\). En règle générale, nous définissons la direction verticale vers le haut comme étant positive. La direction horizontale positive est généralement définie selon la direction du mouvement de l’objet. Lorsque c’est le cas, l’accélération verticale, \(g\), prend une valeur négative (puisqu’il est dirigé vers le bas vers la Terre).

Cependant, il est parfois utile de définir les coordonnées différemment. Par exemple, si vous analysez le mouvement d’une balle lancée vers le bas depuis le haut d’une falaise, il peut être judicieux de définir la direction positive vers le bas puisque le mouvement de la balle se fait uniquement vers le bas. Si c’est le cas, \(g\) prend une valeur positive.

Exemple : Calcul du mouvement du projectile : Projectile de roche chaude

Le Kilauea à Hawaï est le volcan le plus actif au monde. Les volcans très actifs éjectent généralement des roches et de la lave incandescentes plutôt que de la fumée et des cendres. Supposons qu’un gros rocher soit éjecté du volcan à une vitesse de \(25.0\,m/s\) et à un angle de \(35.0°\) au-dessus de l’horizontale, comme le montre la ci-dessous. La roche frappe le flanc du volcan à une altitude de \(20.0\,m\) inférieure à son point de départ.

1. Calculez le temps qu’il faut à la roche pour suivre ce chemin.

2. Quelles sont l’amplitude et la direction de la vitesse de la roche à l’impact ?

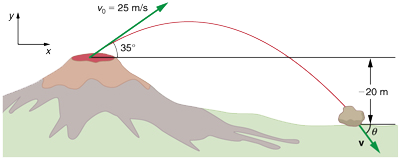
Fig. 8.8 La trajectoire d’une roche éjectée du volcan Kilauea. (crédit : openstax.org)

stratégie

Encore une fois, la décomposition de ce mouvement bidimensionnel en deux mouvements unidimensionnels indépendants nous permettra de trouver les quantités souhaitées. Le temps qu’un projectile passe en l’air est uniquement régi par son mouvement vertical. Nous allons chercher le temps \(t\) en premier. Pendant que la roche monte et descend verticalement, le mouvement horizontal continue à une vitesse constante. Pour la vitesse finale, les résultats verticaux et horizontaux seront recombinés pour obtenir \(v\) et \(\theta\) au temps \(t\) trouvé dans la première partie de l’exemple.

solution

Solution 1.

Pendant que la roche est dans les airs, elle s’élève puis retombe jusqu’à une position finale \(20\,m\) plus bas que son altitude de départ. Nous pouvons trouver le temps mis par le rocher en utilisant :

\[y=y_{0}+v_{0y}t-\dfrac{1}{2}gt^{2}\]

Si nous prenons la position initiale \(y_{0}\) à zéro, alors la position finale est \(y=-20,0\,m\). Maintenant, la vitesse verticale initiale est la composante verticale de la vitesse initiale, trouvée à partir de \(v_{0y}=v_{0}\sin\theta=(25.0\,m/s)\sin 35°\). Ce qui nous donne :

\[(-20\,m)=0+(14.3\,m/s)t-\dfrac{1}{2}(9.81\,m/s^{2})t^{2}\]

La réorganisation des termes donne une équation du \(2^{e}\) degré en \(t\) :

\[(-4.9\,m/s^{2})t^{2}+(14.3\,m/s)t-(20\,m)=0\]

Cette équation donne deux solutions : \(t=3,96\,s\) et \(t=-1,03\,s\).
(Solutions à vérifier en exercice.)
La valeur négative du temps implique un événement avant le début du mouvement, et nous l’écartons donc. Ainsi,

\[t=3,96\,s\]

Solution 2.

A partir des informations maintenant en main, nous pouvons trouver les vitesses horizontales et verticales finales \(v_{x}\) et \(v_{y}\) et les combiner pour trouver la vitesse totale \(v\) et l’angle \(\theta\) fait avec l’horizontale.

La vitesse \(v_{x}\) est constante et nous avons choisi le point de départ pour la calculer car nous connaissons à la fois la vitesse initiale et l’angle initial. Par conséquent :

\[v_{x}=v_{0}\cos\theta=(25\,m/s)(\cos 35°)=20.5\,m/s\]

La vitesse verticale finale est donnée par l’équation \(v_{y}=v_{0y}-gt\) ou \(v_{0}\) a été calculé dans la partie (a): \(v_{0}=14.3\,m/s\). Ainsi,

\[v_{y}=v_{0y}-gt=(14.3\,m/s)-(9.81\,m/s^{2})(3.96\,s)=-24.5\,m/s\]

Pour trouver l’amplitude de la vitesse finale \(v\) on combine ses composantes perpendiculaires, en utilisant Pythagore :

\[v=\sqrt{v_{x}^{2}+v_{y}^{2}}=\sqrt{(20.5\,m/s)^{2}+(-24.5\,m/s)^{2}}=31.9\,m/s\]

L’angle d’impact \(\theta\) se trouve par trigonométrie :

\[\theta_{v}=\tan^{-1}\left(\dfrac{v_{y}}{v_{x}}\right)=\tan^{-1}\left(\dfrac{-24.5}{20.5}\right)=-50.1°\]

discussion

Discussion 1.

Le temps de mouvement du projectile est entièrement déterminé par le mouvement vertical. Ainsi, tout projectile qui a une vitesse verticale initiale de 14,3 m/s et atterrit \(20\,m\) en dessous de son altitude de départ passera \(3.96\,s\) dans les airs.

Discussion 2.

L’angle négatif signifie que la vitesse est \(50.1°\) sous l’horizontale. Ce résultat est cohérent avec le fait que la vitesse verticale finale est négative et donc vers le bas, comme on peut s’y attendre car l’altitude finale est inférieure de \(20.0\,m\) à l’altitude initiale. (Voir Fig. 8.8.)

L’une des choses les plus importantes illustrées par le mouvement des projectiles est que les mouvements verticaux et horizontaux sont indépendants les uns des autres. Galilée a été la première personne à comprendre pleinement cette caractéristique. Il l’a utilisé pour prédire la portée d’un projectile. Sur un terrain plat, nous définissons la portée comme étant la distance horizontale \(R\) parcourue par un projectile. Galilée et bien d’autres s’intéressaient à la portée des projectiles principalement à des fins militaires. Cependant, l’étude de la portée des projectiles peut éclairer d’autres phénomènes intéressants, tels que les orbites des satellites autour de la Terre. Regardons un plus loin la notion de portée d’un projectile.

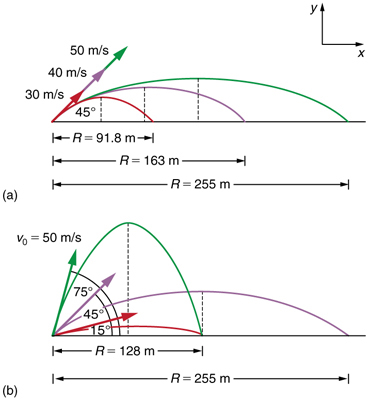
Fig. 8.9 Trajectoires de projectiles sur terrain plat. (a) Plus la vitesse initiale \(v_{0}\) est grande , plus la portée est grande pour un angle initial donné. (b) L’effet de l’angle initial \(\theta_{0}\) sur la portée d’un projectile avec une vitesse initiale donnée. Notez que la portée est la même pour \(15°\) et \(75°\), bien que les hauteurs maximales de ces trajectoires soient différentes. (crédit : openstax.org)

Comment la vitesse initiale d’un projectile affecte-t-elle sa portée? Évidemment, plus la vitesse initiale \(v_{0}\) est grande, plus la portée est grande, comme le montre la Fig. 8.9(a). L’angle initial \(\theta_{0}\) a également un effet considérable sur la portée, comme illustré à la Fig. 8.9(b). Pour une vitesse initiale fixe, telle que pourrait produire un canon, la portée maximale est obtenue avec \(\theta_{0}=45°\). Ceci n’est vrai que pour les conditions négligeant la résistance de l’air. Si la résistance de l’air est prise en compte, l’angle maximal est d’environ \(\theta_{0}=38°\). Fait intéressant, pour chaque angle initial sauf \(45°\), il y a deux angles qui donnent la même plage - la somme de ces angles est toujours \(90°\). La portée dépend également de la valeur de l’accélération de la pesanteur \(g\). L’astronaute lunaire Alan Shepard a pu lancer une balle de golf sur une grande distance sur la Lune car la gravité y est plus faible. La portée \(R\) d’un projectile sur un sol plat pour lequel la résistance de l’air est négligeable est donnée par :

\[R=\dfrac{v_{0}^{2}\sin 2\theta_{0}}{g}\]

où \(v_{0}\) est la vitesse initiale et \(\theta_{0}\) est l’angle initial par rapport à l’horizontale. La preuve de cette équation sera laissée comme exercice, mais elle correspond aux principales caractéristiques de la portée du projectile telles que décrites.

Lorsque nous parlons de la portée d’un projectile sur un terrain plat, nous supposons que \(R\) est très petit par rapport à la circonférence de la Terre. Si, cependant, la portée est grande, la Terre s’incurve sous le projectile et l’accélération de la gravité change de direction le long de la trajectoire. La portée est plus grande que prévu par l’équation de portée donnée ci-dessus parce que le projectile doit tomber plus loin qu’il ne le ferait sur un sol plat. (Voir Fig. 8.10.) Si la vitesse initiale est suffisamment grande, le projectile se met en orbite. Cette possibilité a été reconnue des siècles avant qu’elle puisse être réalisée. Lorsqu’un objet est en orbite, la Terre s’éloigne du dessous de l’objet à la même vitesse qu’elle tombe. L’objet tombe donc continuellement mais ne touche jamais la surface. Ces aspects et d’autres du mouvement orbital, tels que la rotation de la Terre, ne seront malheureusement pas traités cette année.

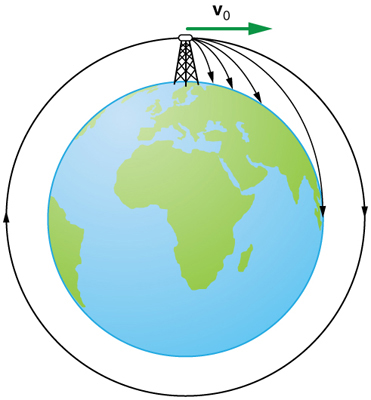
Fig. 8.10 A partir de cette tour théorique, un projectile est lancé depuis une tour très haute pour éviter la résistance de l’air. Avec l’augmentation de la vitesse initiale, la portée augmente et devient plus longue qu’elle ne le serait sur un sol plat car la Terre s’incurve sous sa trajectoire. Avec une vitesse initiale suffisamment grande, l’orbite est atteinte. (crédit : openstax.org)

PhET simulation

Projectile motion

YouTube

Alan Shepard Hits A Golf Ball on the Moon