7.1. Gravité et chute libre

La chute libre

Les objets qui tombent forment une classe intéressante de problèmes de mouvement. Par exemple, nous pouvons estimer la hauteur d’une falaise vertical en y laissant tomber un rocher et en écoutant le rocher toucher le fond. En appliquant la cinématique développée jusqu’à présent aux chutes d’objets, nous pouvons examiner certaines situations intéressantes et en apprendre beaucoup sur la gravité dans le processus.

La gravité

Le fait le plus remarquable et le plus inattendu concernant la chute d’objets est que, si la résistance de l’air et le frottement sont négligeables, alors à un endroit donné, tous les objets tombent vers le centre de la Terre avec la même accélération constante, indépendamment de leur masse. Ce fait déterminé expérimentalement est inattendu, car nous sommes tellement habitués aux effets de la résistance de l’air et du frottement que nous nous attendons à ce que les objets légers tombent plus lentement que les lourds.

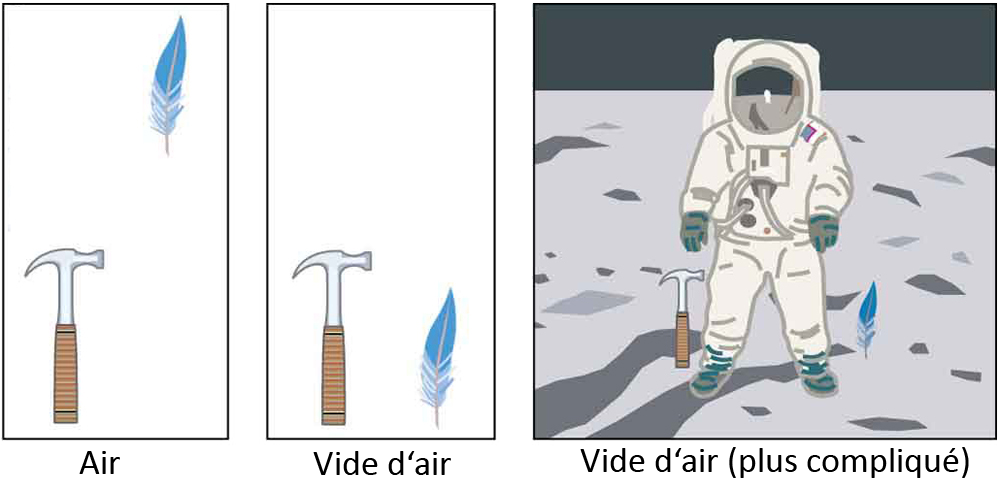
Fig. 7.1 Un marteau et une plume tomberont avec la même accélération constante si la résistance de l’air est considérée comme négligeable. C’est une caractéristique générale de la gravité qui n’est pas propre à la Terre, comme l’a démontré l’astronaute David R. Scott sur la Lune en 1971, où l’accélération due à la gravité n’est que \(1.67\,m/s^{2}\). (crédit : openstax.org)

YouTube

Chute d’une plume et d’un marteau sur la Lune - Apollo 15 - 1971 - David Scott et James Irwin

Dans le monde réel, la résistance de l’air peut faire tomber un objet plus léger plus lentement qu’un objet plus lourd de même taille. Une balle de tennis atteindra le sol après qu’une balle de baseball dure ait chuté en même temps. (Il peut être difficile d’observer la différence si la hauteur n’est pas grande.) La résistance de l’air s’oppose au mouvement d’un objet dans l’air, tandis que la friction (frottements) entre les objets, comme entre les pneus d’une voiture et la route, s’oppose au mouvement entre eux. Pour les situations idéales de ces premières leçon, un objet tombant sans résistance à l’air ni frottement est défini comme étant en chute libre.

La force de gravité fait tomber les objets vers le centre de la Terre. L’accélération des objets en chute libre est donc appelée accélération due à la gravité. L’accélération due à la gravité est constante, ce qui signifie que nous pouvons appliquer les équations cinématiques à tout objet en chute où la résistance de l’air et le frottement sont négligeables. Cela nous ouvre une large classe de situations intéressantes. L’accélération due à la gravité est si importante que sa magnitude reçoit son propre symbole, \(g\).
Elle varie très peu d’un endroit à un autre sur Terre et a la valeur moyenne de:

\[g=9.81\,\left[ m/s^{2}\right]\]

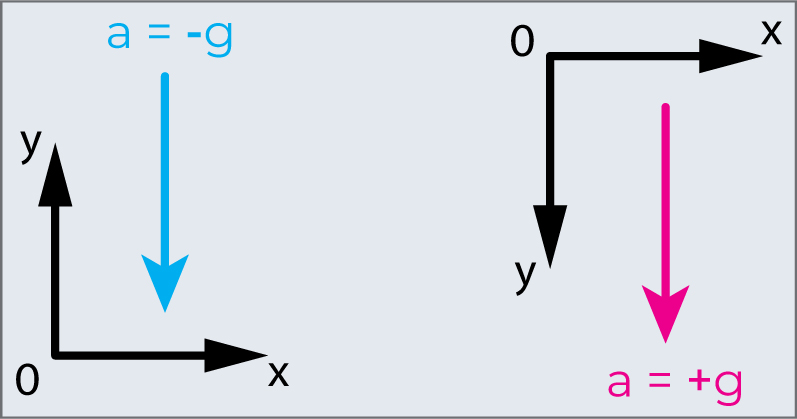
Bien que \(g\) varie de \(9.78\,m/s^{2}\) à \(9.83\,m/s^{2}\) en fonction de la latitude, de l’altitude, des formations géologiques sous-jacentes et de la topographie locale, la valeur moyenne de \(9.81\,m/s^{2}\) sera utilisé dans ce texte sauf indication contraire. La direction de l’accélération due à la gravité est vers le bas (vers le centre de la Terre). En fait, sa direction définit ce que nous appelons vertical. Notez que l’accélération \(a\), dans les équations cinématiques, prend la valeur \(+g\) ou \(-g\) en fonction de la façon dont nous définissons notre système de coordonnées. Si nous définissons la direction ascendante comme négative, alors \(a=-g=-9.81\,m/s^{2}\) et si nous définissons la direction descendante comme positive, alors \(a=g=9.81\,m/s^{2}\)

Mouvement unidimensionnel impliquant la gravité

La meilleure façon de voir les caractéristiques de base du mouvement impliquant la gravité est de commencer par les situations les plus simples, puis de progresser vers des situations plus complexes. Nous commençons donc par considérer un mouvement droit de haut en bas sans résistance à l’air ni frottement. Ces hypothèses signifient que la vitesse (s’il y en a) est verticale. Si l’objet tombe, nous savons que la vitesse initiale est nulle. Une fois que l’objet a quitté le contact avec ce qui l’a tenu ou l’a lancé, l’objet est en chute libre. Dans ces circonstances, le mouvement est unidimensionnel et a une accélération constante d’amplitude \(g\). Nous représenterons également le déplacement vertical avec le symbole \(y\) et utiliserons \(x\) pour le déplacement horizontal.

Équations de la cinématique

Équations de la cinématique pour les objets en chute libre (\(\boldsymbol{a=\pm\,g}\)) :

\[\begin{split}\begin{align*} v(t) &=v_{0}\pm g\cdot t\\ y(t) &=y_{0}+v_{0}\cdot t\pm \dfrac{1}{2}g\cdot t^{2}\\ v^{2} &=v_{0}^{2}\pm 2g\cdot (y(t)-y_{0}) \end{align*}\end{split}\]

Le signe \(\pm\) de \(g\) dépendra du sens de l’axe de référence.

Exemple 1 : Calculer la vitesse d’un objet qui tombe - Une pierre lâchée

Un caillou est lâché du haut d’un gratte-ciel.
Quelle est la vitesse du caillou après \(t=2.35\,s\) de chute ?

solution

En supposant que la verticale est orientée positivement vers le haut, les variables connues sont :

• La vitesse initiale \(v_{0}=0\,m/s\) car le caillou démarre au repos (il est lâché)

• Le temps \(t=2.35\,s\) à la fin duquel on veut déterminer la vitesse

• L’accélération \(a_{g}=-9.81\,m/s^{2}\) qui est imposés par le mouvement de chute libre du caillou

Dans cette situation, le mouvement est vertical, on utilise donc \(y\) comme variable de position plutôt que \(y\). Le symbole choisi a peu d’importance dès lors qu’on reste cohérent, mais en pratique, c’est très souvent \(y\) qu’on utilise pour décrire les mouvements verticaux.

Puisqu’on ne connait pas le déplacement \(\Delta y\) et puisque le déplacement \(\Delta y\) n’est pas non plus demandé, on utilise la première équation cinématique: \(v=a\cdot t+v_{0}\), dans laquelle \(\Delta y\) n’apparaît pas.

On a donc

\[v=a_{g}\cdot t+v_{0}=-9.81\,m/s^{2}\cdot 2.35\,s+0\,m/s=-23.1\,m/s\]

discussion

La vitesse finale est négative puisque le caillou se dirige vers le bas.

Exemple 2 : Calculer la position et la vitesse d’un objet qui tombe - Une pierre projetée vers le haut

Une personne debout au bord d’une haute falaise jette un rocher verticalement vers le haut avec une vitesse initiale de \(13.0\,m/s\). Le rocher manque le bord de la falaise alors qu’il retombe sur terre.
Calculez la position et la vitesse du rocher \(1,00\,s\), \(2,00\,s\) et \(3,00\,s\) après son lancement, en négligeant les effets de la résistance de l’air.

stratégie

Dessinez un croquis.

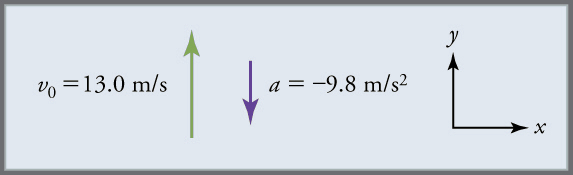
On nous demande de déterminer la position \(y(t)\) à différents moments \(t\). Il est raisonnable de prendre la position initiale \(y_{0}\) nulle. Ce problème implique un mouvement unidimensionnel dans la direction verticale. Nous utilisons des signes plus et moins pour indiquer la direction, le haut étant positif et le bas négatif. Puisque le haut est positif et que la pierre est projetée vers le haut, la vitesse initiale doit également être positive. L’accélération due à la gravité est vers le bas, donc elle est négative. Il est essentiel que la vitesse initiale et l’accélération due à la gravité aient des signes opposés. Des signes opposés indiquent que l’accélération due à la gravité s’oppose au mouvement initial et le ralentira.

Puisqu’on nous demande des valeurs de position et de vitesse à trois moments, nous nous référons à celles-ci comme \(y_{1}\) et \(v_{1}\); \(y_{2}\) et \(v_{2}\) et \(y_{3}\) et \(v_{3}\).

solution

Pour la position :

1. Identifiez les éléments connus. Nous savons que \(y_{0}=0\,m\) et \(v_{0}=13\,m/s\); \(a=-g=-9.81\,m/s^{2}\) et \(t=1.00\,s\).

2. Identifiez la meilleure équation à utiliser. Nous utiliserons \(y(t)=y_{0}+v_{0}\cdot t+\dfrac{1}{2}a\cdot t^{2}\) car elle ne comprend qu’une seule inconnue, \(y(t)\) (ou \(y=(t=1\,s)=y_{1}\), ici), qui est la valeur que nous voulons trouver.

3. Appliquez les valeurs numériques et trouvez \(y_{1}\).

\[\begin{split}\begin{align*} y_{1} &=0+(13.0\,m/s)(1.00\,s)+\dfrac{1}{2}(-9.81\,m/s^{2})(1.00\,s)^{2}\\ y_{1} &=8.10\,m \end{align*}\end{split}\]

Pour la vitesse :

Le rocher est à \(8.10\,m\) au-dessus de son point de départ à \(t=1.00\,s\), puisque \(y_{1}>y_{0}\). Il peut s’agir d’un mouvement vers le haut ou vers le bas; la seule façon de dire est de calculer \(v_{1}\) et découvrir si elle est positive ou négative.

1. Identifiez les éléments connus. Nous savons que \(y_{0}=0\,m\), \(v_{0}=13\,m/s\), \(a=-g=-9.81\,m/s^{2}\) et \(t=1.00\,s\). Nous savons également de la solution ci-dessus que \(y_{1}=8.10\,m\).

2. Identifiez la meilleure équation à utiliser. La plus simple est \(v =v_{0}-g\cdot t\).

3. Appliquez les valeurs numériques et trouvez \(v_{1}\).

\[v_{1}=13.0\,m/s-(9.81\,m/s^{2})(1.00\,s)=3.20\,m/s\]

La valeur positive pour \(v_{1}\) signifie que le rocher se dirige toujours vers le haut à \(t=1.00\,s\). Cependant, il a ralenti par rapport à ses \(13.0\,m/s\) de départ, comme prévu.

Solution finale :

Les procédures de calcul de la position et de la vitesse à \(t=2.00\,s\) et \(t=3.00\,s\) sont les mêmes que ceux ci-dessus. Les résultats sont résumés dans le tableau ci-dessous :

Temps \(t\) \([s]\)	Position \(y\) \([m]\)	Vitesse \(v\) \([m/s]\)	Accélération \(a\) \([m/s^{2}]\)
1.00	8.10	3.20	-9.81
2.00	6.40	-6.60	-9.81
3.00	-5.10	-16.40	-9.81

La représentation graphique des données nous aide à les comprendre plus clairement.

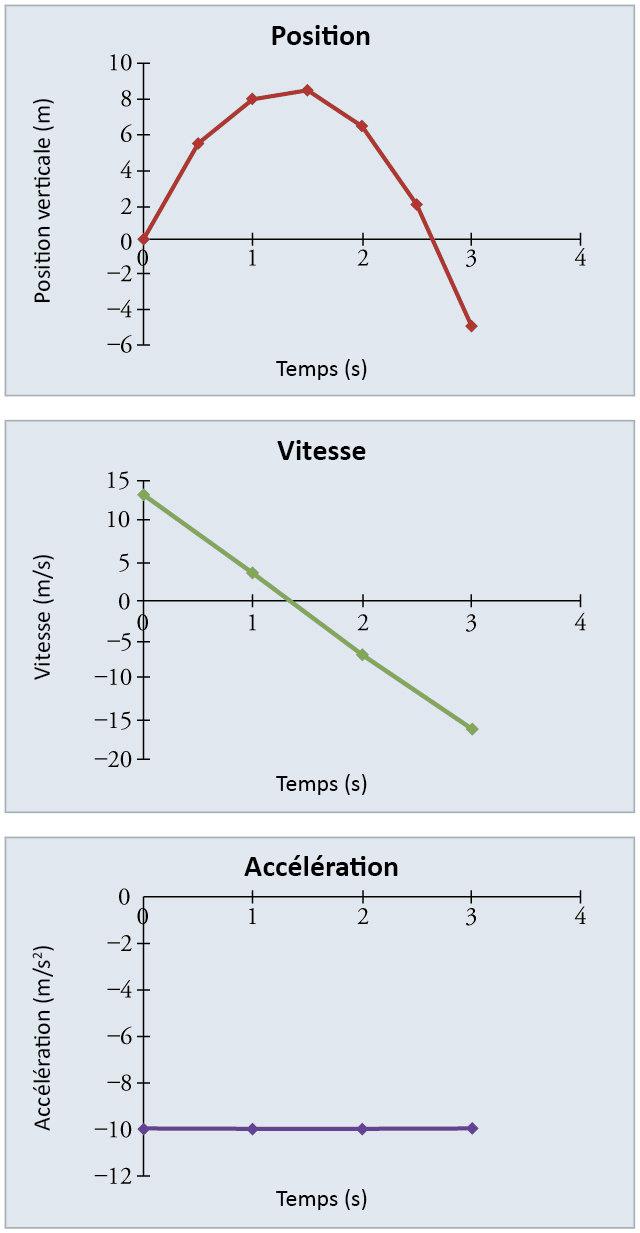
Fig. 7.2 Position verticale, vitesse verticale et accélération verticale en fonction du temps pour un rocher projeté verticalement au bord d’une falaise. Notez que la vitesse change linéairement avec le temps et que l’accélération est constante. Alerte aux idées fausses! Notez que le graphique de position en fonction du temps montre uniquement la position verticale. Il est facile d’avoir l’impression que le graphique montre un mouvement horizontal - la forme du graphique ressemble à la trajectoire d’un projectile. Mais ce n’est pas le cas; l’axe horizontal est le temps, pas l’espace. Le chemin réel du rocher dans l’espace est droit vers le haut et vers le bas.

discussion

L’interprétation de ces résultats est importante.

À \(t=1.00\,s\), le rocher est au-dessus de son point de départ et se dirige vers le haut, car \(y_{1}\) et \(v_{1}\) sont tous les deux positifs.

À \(t=2.00\,s\), le rocher est toujours au-dessus de son point de départ, mais la vitesse négative signifie qu’il se déplace vers le bas.

À \(t=3.00\,s\), les deux \(y_{3}\) et \(v_{3}\) sont négatifs, ce qui signifie que le rocher est en dessous de son point de départ et continue de se déplacer vers le bas.

Notez que lorsque le rocher est à son point le plus élevé (à \(1.50\,s\)), sa vitesse est nulle, mais son accélération est toujours \(-9.81\,m/s^{2}\). Son accélération est \(-9.81\,m/s^{2}\) pendant tout le trajet - pendant qu’il monte et pendant qu’il descend.

Notez que les valeurs de \(y\) sont les positions (ou déplacements) du rocher et non les distances totales parcourues.

Enfin, notez que la chute libre s’applique aussi bien aux mouvements ascendants qu’à ceux descendants. Les deux ont la même accélération - l’accélération due à la gravité, qui reste constante tout le temps.

Exemple 3: Calculer la vitesse d’un objet qui tombe - Une pierre lancée vers le bas

Que se passe-t-il si la personne sur la falaise jette le rocher directement vers le bas, au lieu de le faire vers le haut? Calculer la vitesse du rocher lorsqu’il est à \(5.10\,m\) en dessous du point de départ, et qu’il a été projetée vers le bas avec une vitesse initiale de \(13.0\,m/s\).

stratégie

Dessinez un croquis.

Puisque le haut est positif, la position finale du rocher sera négative car elle se termine en dessous du point de départ à \(y_{0}=0\). De même, la vitesse initiale est descendante et donc négative, tout comme l’accélération due à la gravité. Nous nous attendons à ce que la vitesse finale soit négative puisque le rocher continuera à se déplacer vers le bas.

solution

1. Identifiez les éléments connus. Nous savons que \(y_{0}=0\,m\), \(y_{1}=5.10\,m\), \(v_{0}=13.0\,m/s\), \(a=-g=-9.81\,m/s^{2}\).

2. Choisissez l’équation cinématique qui facilite la résolution du problème. L’équation \(v^{2}=v_{0}^{2}-2g\Delta y\) fonctionne bien car on ne connaît pas le temps \(t\) et on cherche \(v_{fin}\).

3. Appliquez les valeurs numériques et résolvez.

\[v_{2}=(-13.0\,m/s)^{2}+ 2(-9.81\,m/s^{2})(-5.10\,m-0\,m)=268.96\,m^{2}/s^{2}\]

où nous avons retenu des chiffres très significatifs car il s’agit d’un résultat intermédiaire.

6. En prenant la racine carrée et en notant qu’une racine carrée peut être positive ou négative, on obtient

\[v=\pm\sqrt{268.96\,m^{2}/s^{2}}=\pm 16.4\,m/s.\]

7. La racine négative est choisie pour indiquer que le rocher est toujours en train de descendre. Donc,

\[v=-16.4\,m/s.\]

discussion

Notez que c’est exactement la même vitesse que le rocher avait à cette position lorsqu’il a été lancée vers le haut avec la même vitesse initiale. (Voir l’exemple 2 et la Fig. 7.3). Ce n’est pas une coïncidence. Parce que nous ne considérons que l’accélération due à la gravité dans ce problème, la vitesse d’un objet qui tombe ne dépend que de sa vitesse initiale et de sa position verticale par rapport au point de départ.

Par exemple, si la vitesse du rocher est calculée à une hauteur de \(8.10\,m\) au-dessus du point de départ (en utilisant la méthode de l’exemple 2) lorsque la vitesse initiale est de \(13.0\,m/s\) vers le haut, un résultat de \(\pm 3.20\,m/s\) Est obtenu. Ici, les deux signes sont significatifs; la valeur positive se produit lorsque le rocher est à \(8.10\,m\) et se dirige vers le haut, et la valeur négative se produit lorsque le rocher est à \(8.10\,m\) et se dirige vers le bas. Il a la même vitesse mais la direction opposée.

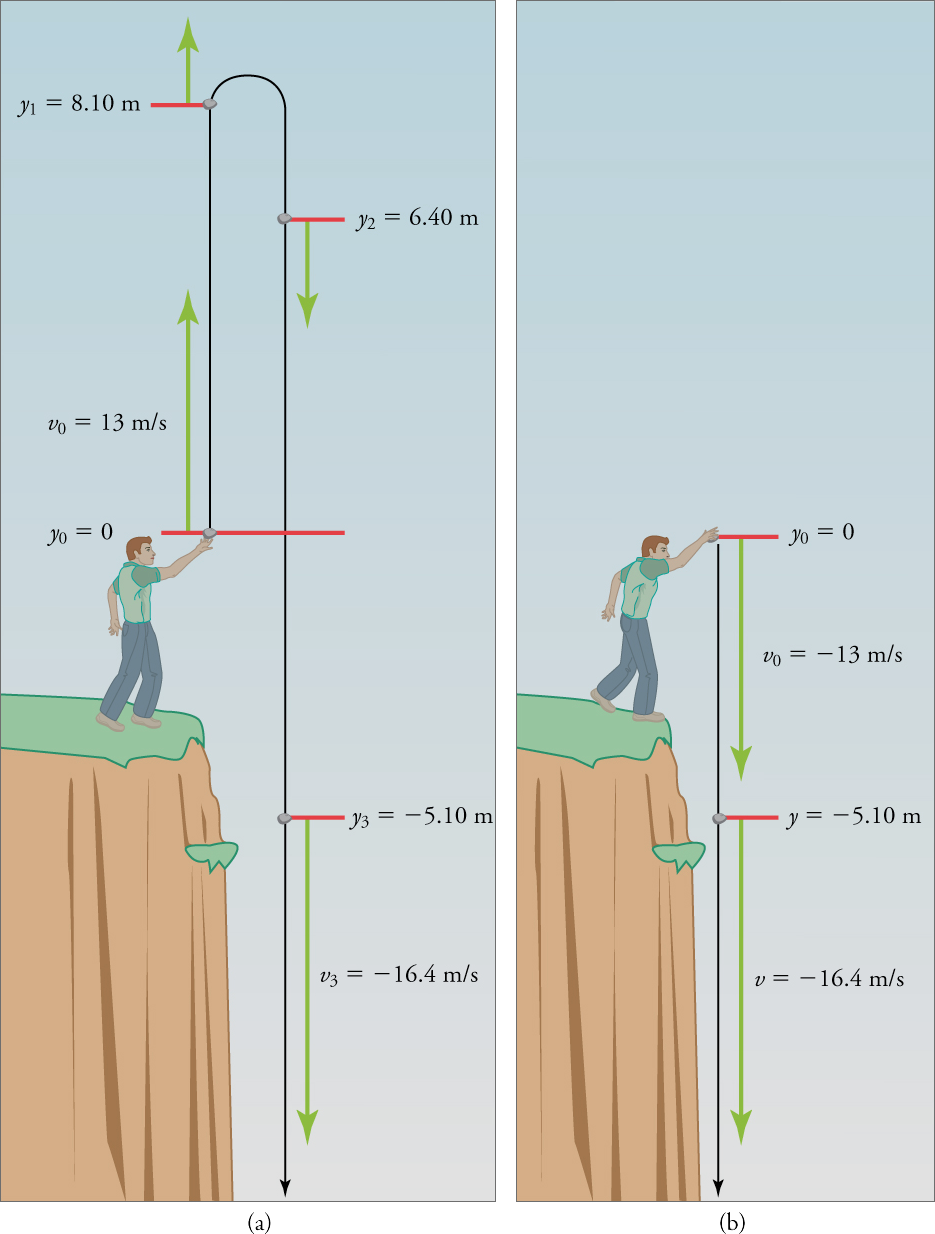
Fig. 7.3 (a) Une personne jette une pierre vers le haut, comme l’explique l’ exemple 2. Les flèches sont des vecteurs de vitesse à 0, 1.00, 2.00 et 3.00 seconde. (b) Une personne jette un rocher directement depuis une falaise avec la même vitesse initiale que précédemment, comme dans l’ exemple 3. Notez qu’à la même distance en dessous du point de sortie, la roche a la même vitesse dans les deux cas. (crédit : openstax.org)

Une autre façon de voir les choses est la suivante : dans l’ exemple 2, le rocher est projetée avec une vitesse initiale de \(13.0\,m/s\). Il monte puis redescend. Quand sa position est \(y=0\,m\) en redescendant, sa vitesse est \(-13.0\,m/s\). Autrement dit, il a la même vitesse en descendant qu’en montant. On s’attend alors à ce que sa vitesse, à une position de \(y=-5.10\,m\), soie la même si nous l’avons jeté vers le haut \(+13.0\,m/s\) ou jeté vers le bas \(-13.0\,m/s\). La vitesse du rocher en descendant de \(y=0\,m\) est la même que nous l’ayons lancé vers le haut ou vers le bas pour commencer, du moment que la vitesse à laquelle il a été lancé initialement est la même.

Exemple 4: Trouver \(g\) à partir des données sur un objet en chute libre

L’accélération due à la gravité sur Terre diffère légèrement d’un endroit à l’autre, en fonction de la topographie (par exemple, que vous soyez sur une colline ou dans une vallée) et de la géologie souterraine (s’il existe une roche dense comme le minerai de fer par opposition à une roche légère comme le sel sous vous).

L’accélération précise due à la gravité peut être calculée à partir des données prises dans un cours de travaux pratique de physique. Un objet, généralement une bille métallique pour laquelle la résistance de l’air est négligeable, tombe et le temps qu’il faut pour tomber à une distance connue est mesuré. Voir, par exemple, la figure ci-dessous.

Des résultats très précis peuvent être obtenus avec cette méthode si un soin suffisant est pris dans la mesure de la distance parcourue et du temps écoulé.

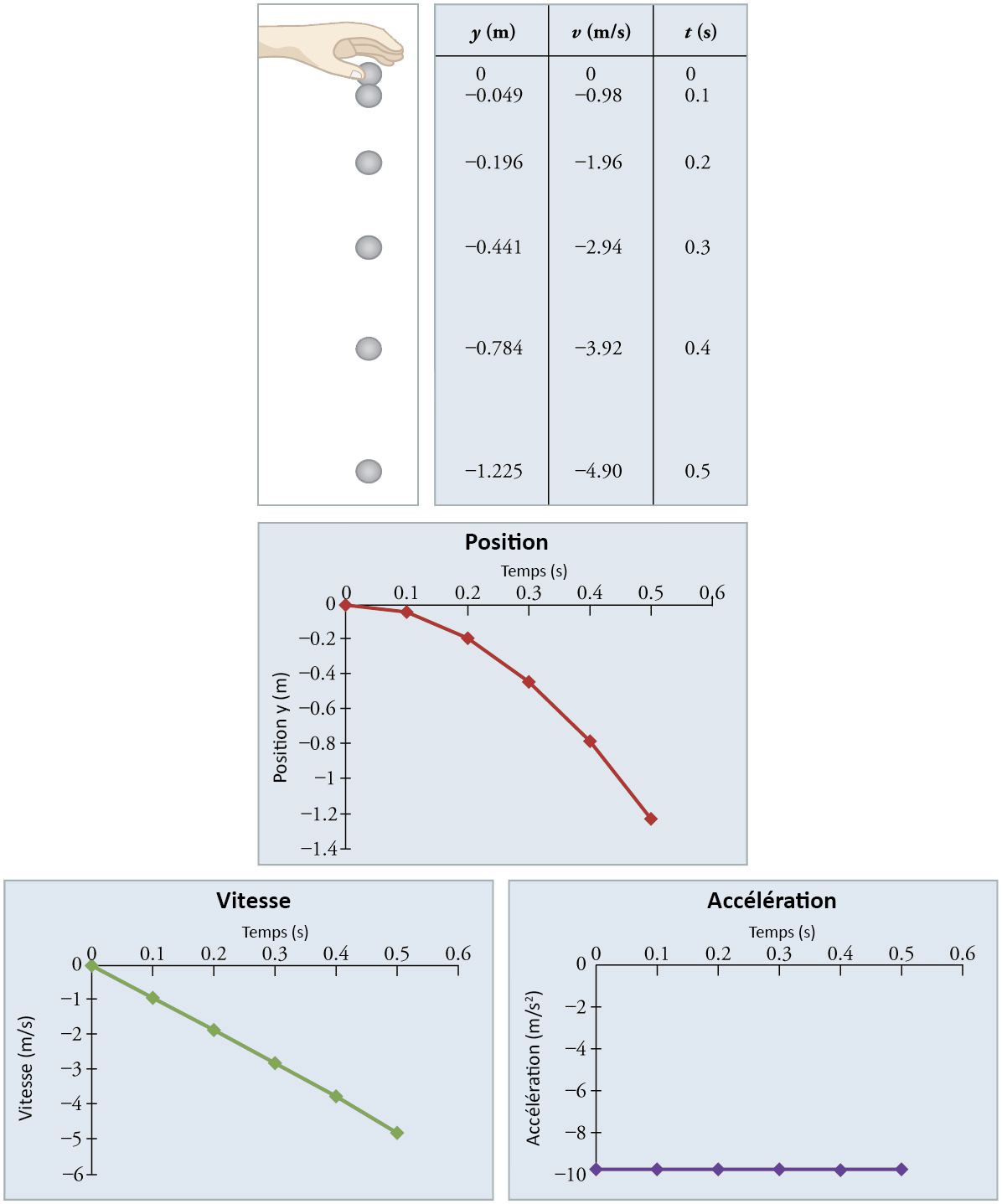
Fig. 7.4 Positions et vitesses d’une bille métallique libérée du repos lorsque la résistance de l’air est négligeable. La vitesse augmente linéairement avec le temps tandis que le déplacement augmente avec le temps au carré. L’accélération est une constante et est égale à l’accélération gravitationnelle. (crédit : openstax.org)

Supposons que la balle tombe de \(1.0000\,m\) en \(0.45155\,s\). En supposant que la balle n’est pas affectée par la résistance de l’air, quelle est l’accélération précise due à la gravité à cet endroit?

stratégie

Dessinez un croquis.

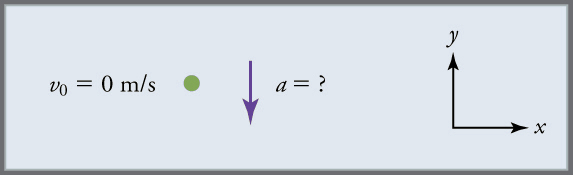
Nous devons résoudre pour l’accélération \(a\). Notez que dans ce cas, le déplacement est vers le bas et donc négatif, tout comme l’accélération.

solution

1. Identifiez les éléments connus. Nous savons que \(y_{0}=0\,m\), \(y_{1}=1.0000\,m\), \(v_{0}=0\,m/s\), \(t=0.45155\,s\).

2. Choisissez l’équation qui vous permet de résoudre une en utilisant les valeurs connues: \(y=y_{0}+v_{0}\cdot t+\dfrac{1}{2}a\cdot t^{2}\)

3. Réorganiser l’équation (avec \(v_{0}=0\,m/s\)):

\[a=\dfrac{2(y-y_{0})}{t^{2}}\]

4. Appliquez les valeurs numériques et résolvez.

\[a=\dfrac{2(-1.0000\,m-0\,m)}{(0.45155\,s)^{2}}=-9.8089\,m/s^{2}\]

alors parce que \(a=-g\) avec les directions que nous avons choisies,

\[g=9.8089\,m/s^{2}\]

discussion

La valeur négative pour \(a\) une indique que l’accélération gravitationnelle est vers le bas, comme prévu. Nous nous attendons à ce que la valeur se situe quelque part autour de la valeur moyenne de \(9.81\,m/s^{2}\), alors \(9.8089\,m/s^{2}\) est logique. Les données entrant dans le calcul étant relativement précises, cette valeur pour \(g\) est plus précise que la valeur moyenne de \(9.81\,m/s^{2}\); elle représente la valeur locale de l’accélération due à la gravité.

Exemple 5: Calculer le temps de chute d’un objet

Un morceau de glace se brise d’un glacier et tombe de \(30.0\) mètres avant de toucher l’eau. En supposant qu’il tombe librement (il n’y a pas de résistance à l’air), combien de temps lui faut-il pour frapper l’eau ?

solution

On connaît :

• la position initiale \(y_{0}=0\,m\)

• la position finale \(y(t)=30.0\,m\)

• la vitesse initiale \(v_{0}=0\,m/s\) et

• l’accélération \(a=-g=-9.81\,m/s^{2}\).

Comme on n’a aucune information sur la vitesse finale \(v(t)\), on peut alors utiliser l’équation \(y=y_{0}+v_{0}\cdot t+\dfrac{1}{2}a\cdot t^{2}\) pour trouver le temps \(t\).
On obtient :

\[\begin{split}\begin{align*} y(t) &=0+0-\dfrac{1}{2}g\cdot t^{2}\\ \Rightarrow\quad t^{2} &=-\dfrac{2y(t)}{g}\\ \Rightarrow\quad t &=\pm\sqrt{-\dfrac{2y(t)}{g}}=\pm\sqrt{-\dfrac{2\cdot (-30.0\,m)}{9.81\,m/s^{2}}}=\pm\sqrt{6.12\,s^{2}}=\pm 2.47\,s\simeq\pm 2.5\,s \end{align*}\end{split}\]

On prend la valeur positive comme réponse physiquement pertinente!
Il faut donc environ \(2.5\) secondes au morceau de glace pour toucher l’eau.