11.5. Force sur une charge en mouvement dans un champ magnétique

Quel est le mécanisme par lequel un aimant exerce une force sur un autre ? La réponse est liée au fait que tout magnétisme est causé par le courant, le flux de charge. Les champs magnétiques exercent des forces sur les charges en mouvement, et donc ils exercent des forces sur d’autres aimants, qui ont tous des charges en mouvement.

Force de Lorentz

La force magnétique sur une charge en mouvement est l’une des plus fondamentales connues. La force magnétique est aussi importante que la force électrostatique (la force de Coulomb). Pourtant, la force magnétique est plus complexe, à la fois dans le nombre de facteurs qui l’affectent et dans sa direction, que la force de Coulomb.

Titre_Formule

L’amplitude de la force magnétique \(F_{magn}\) sur une charge \(q\) se déplaçant à une vitesse \(v\) dans un champ magnétique d’intensité \(B\) est donnée par :

(11.1)\[F_{magn}=q\cdot v\cdot B\cdot\sin\theta\]

où \(\theta\) est l’angle entre les directions de \(v\) et \(B\)

Cette force est souvent appelée force de Lorentz. En fait, c’est ainsi que nous définissons l’intensité du champ magnétique, c’est-à-dire la force exercée sur une particule chargée se déplaçant dans un champ magnétique.

L’unité SI pour l’intensité du champ magnétique est appelée Tesla (\([\text{T}]\)) d’après l’excentrique mais brillant inventeur Nikola Tesla (1856-1943). Pour déterminer comment le Tesla se rapporte aux autres unités SI, nous résolvons l’équation (11.1) pour \(B\) :

\[\begin{split}F=qvB\sin\theta\\ B=\dfrac{F}{qv\sin\theta}\end{split}\]

Puisque \(\sin\theta\) est sans unité, l’unité Tesla est définie par :

\[1\,\text{T}=\dfrac{1\,\text{N}}{1\,\text{C}\cdot 1\,\text{m/s}}=\dfrac{1\,\text{N}}{1\,\text{A}\cdot 1\,\text{m}}=1\,\dfrac{\text{N}}{\text{A}\cdot \text{m}}\]

Règle de la main droite

La direction de la force magnétique est toujours perpendiculaire au plan formé par \(v\) et \(b\). La règle de la main droite, qui est illustrée à la Fig. 11.14 permet de déterminer la direction de la force magnétique, de la vitesse ou du champ magnétique. La règle de la main droite stipule que, pour déterminer la direction de la force magnétique sur une charge mobile positive, vous pointez le pouce de la main droite dans la direction de \(v\), les doigts dans la direction de \(B\), et la direction perpendiculaire à la paume pointera dans la direction de \(F\). Une façon de s’en souvenir est qu’il n’y a que une vitesse, et donc le pouce la représente. Il y a beaucoup de lignes de champ, et donc les doigts les représentent. La force est dans la direction dans laquelle vous pousseriez avec votre paume.
Si la charge \(q\) est négative, alors le force sera aussi négative. Elle pointera dans l’autre direction. La force exercée sur une charge négative est exactement dans la direction opposée à celle exercée sur une charge positive.

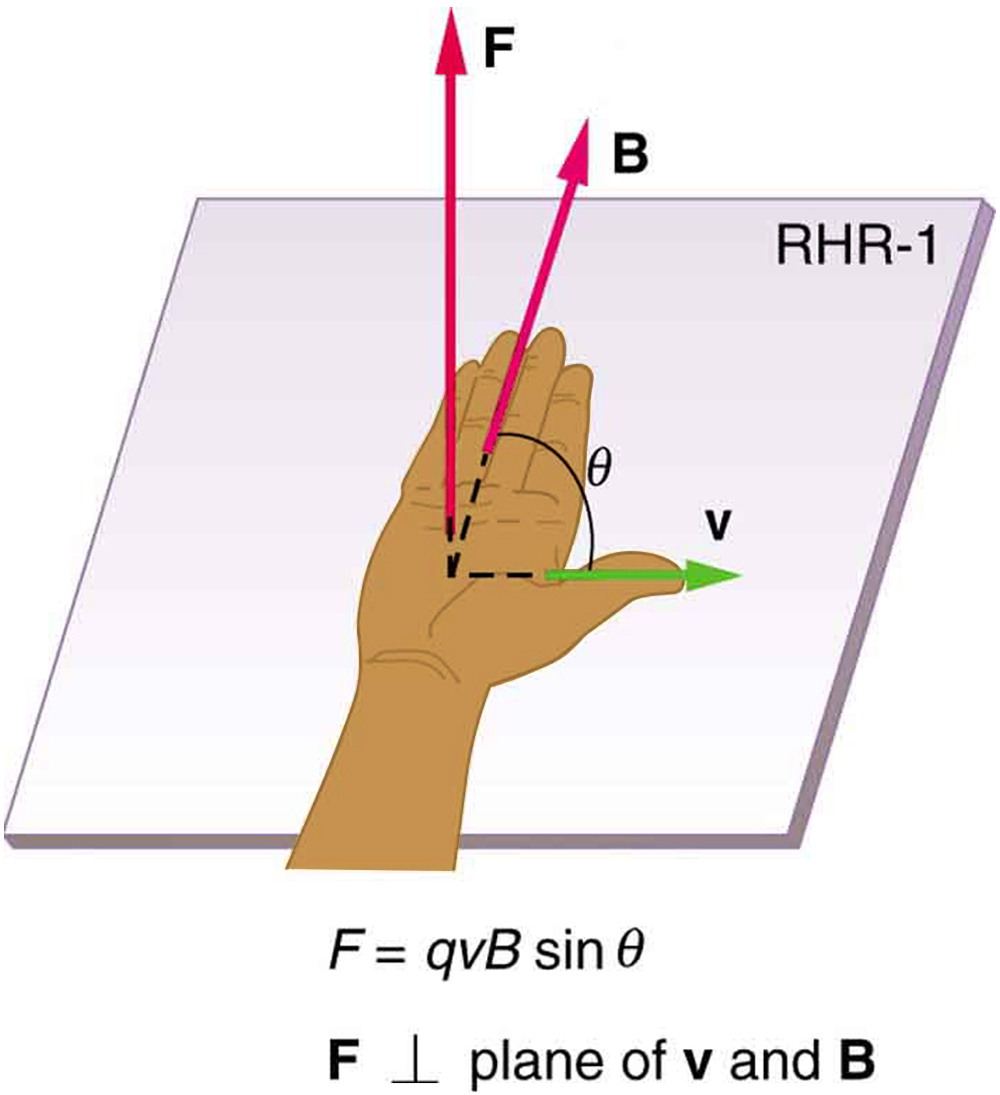
Fig. 11.14 Les champs magnétiques exercent des forces sur les charges en mouvement. Cette force est l’une des plus fondamentales connues. La direction de la force magnétique sur une charge en mouvement est perpendiculaire au plan formé par \(v\) et \(B\) et suit la règle de la main droite comme indiqué. L’amplitude de la force est proportionnelle à \(q\), \(v\), \(B\) et au sinus de l’angle entre \(v\) et \(B\).

Établir des connexions : charges et aimants

Il n’y a pas de force magnétique sur les charges statiques. Cependant, il existe une force magnétique sur les charges en mouvement. Lorsque les charges sont stationnaires, leurs champs électriques n’affectent pas les aimants. Mais, lorsque les charges se déplacent, elles produisent des champs magnétiques qui exercent des forces sur d’autres aimants. Lorsqu’il y a un mouvement relatif, une connexion entre les champs électriques et magnétiques émerge - chacun affecte l’autre.

Exemple : Calcul de la force magnétique

Calcul de la force magnétique : champ magnétique terrestre sur une tige de verre chargée À l’exception des boussoles, vous voyez ou ressentez rarement les forces dues au petit champ magnétique de la Terre. Pour illustrer cela, supposons que dans un laboratoire de physique, vous frottiez une tige de verre avec de la soie, en plaçant une charge positive de \(20\,nC\) dessus. Calculez la force exercée sur la tige par le champ magnétique terrestre, si vous la lancez avec une vitesse horizontale de \(10\,m/s\) plein ouest à un endroit où le champ terrestre est plein nord parallèlement au sol.
(La direction de la force est déterminée par la règle de la main droite comme indiqué dans la Fig. 11.15 et la valeur du champs magnétique terrestre est de \(B_{Terre}=5\cdot 10^{-5}\,\text{T}\).)

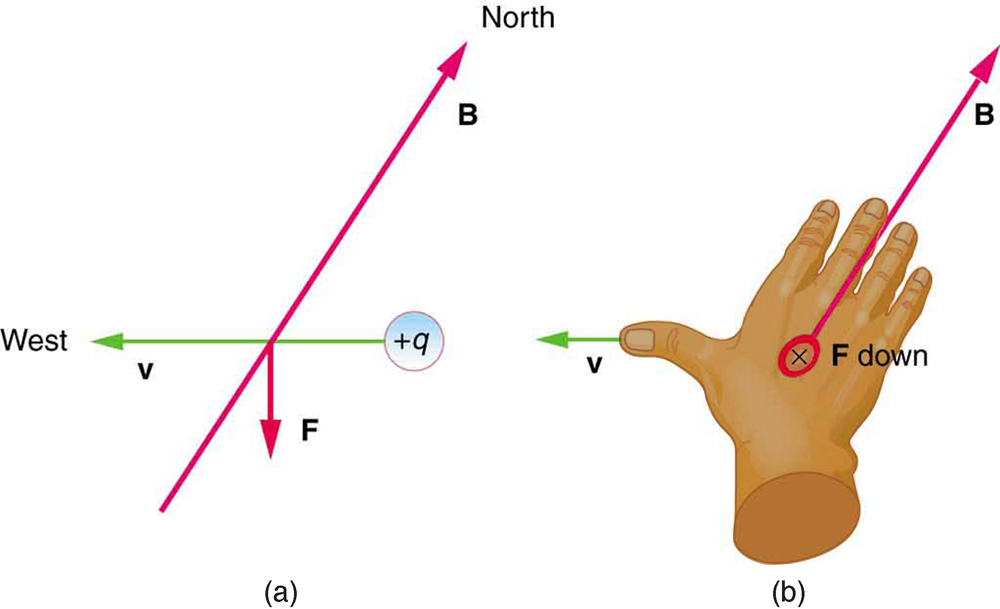
Fig. 11.15 Un objet chargé positivement se déplaçant plein ouest dans une région où le champ magnétique terrestre est plein nord subit une force qui est droite vers le bas, comme indiqué. Une charge négative se déplaçant dans la même direction ressentirait une force vers le haut.

stratégie

On nous donne la charge, sa vitesse, ainsi que l’intensité et la direction du champ magnétique. On peut donc utiliser l’équation \(F=qvB\sin\theta\) pour trouver la force.

solution

Puisque l’angle \(\theta\) entre la vitesse et la direction du champ est de \(90°\), \(\sin\theta=1\). La saisie des autres quantités données donne :

\[F=(20\cdot 10^{-9}\,\text{C})\cdot (10\,m/s)\cdot (5\cdot 10^{-5}\,\text{T})= 1\cdot 10^{-11}\,\text{N}\]

discussion

Cette force est totalement négligeable sur n’importe quel objet macroscopique, ce qui est cohérent avec l’expérience. (Il est calculé à un seul chiffre significatif, car le champ terrestre varie selon l’emplacement et n’est donné qu’à un seul chiffre.) Le champ magnétique terrestre produit cependant des effets très importants, en particulier sur les particules submicroscopiques.

Exemples et applications

TO DO