3.1. Position et Déplacement#
La position#
En physique, il est important de décrire précisément le mouvement des objets. C’est généralement le sujet des premiers chapitres des livres de physique dans la mesure où c’est une base de cette science. Décrire le mouvement d’un objet n’est pas forcément facile. Par exemple, une personne qui fait la sieste sous un arbre est immobile par rapport à l’arbre, mais en mouvement par rapport au soleil.
Pour décrire le mouvement d’un objet, il faut d’abord décrire la position de cet objet, c’est à dire décrire où il se trouve à un instant donné. Plus précisément, il nous faut spécifier sa position par rapport à un point de référence (un objet immobiles sur terre, l’origine des axes,…) bien choisi. Par exemple, la position d’une enseignante peut être décrite par rapport au tableau à côté duquel elle se trouve (Fig. 3.1).
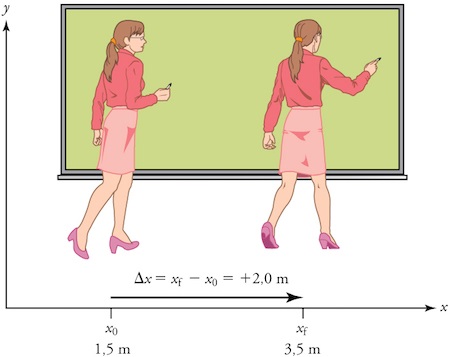
Fig. 3.1 L’enseignante se déplace devant le tableau pendant son cours. Son déplacement de \(+2.0\,m\) dans le référentiel terrestre est représenté par une flèche pointant vers la droite. (crédit: openstax.org)#
Dans certains cas, on utilise des référentiels mobiles par rapport à la Terre. Par exemple, on utilise le référentiel de l’avion (en mouvement par rapport à la Terre) pour décrire la position d’une personne qui se déplace à l’intérieur (Fig. 3.2).
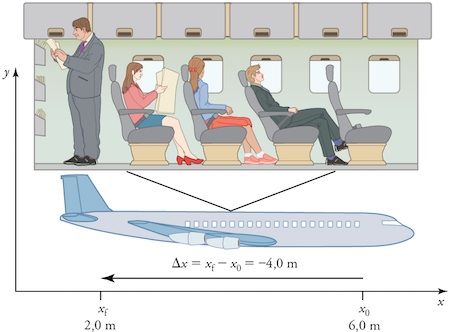
Fig. 3.2 Un passager se déplace de son siège vers l’arrière de l’avion. Le déplacement de \(-4.0\,m\) du passager dans le référentiel de l’avion est représenté par une flèche pointant vers l’arrière de l’avion. (crédit: openstax.org)#
En général, la variable \(x\) représente la position horizontale, et la variable \(y\) représente la position verticale.
Le déplacement#
Si un objet bouge dans un référentiel (par exemple, l’enseignante qui se déplace vers la droite par rapport au tableau, ou encore, le passager qui se déplace vers l’arrière de l’avion), cela signifie que sa position varie. Ce changement de position s’appelle le déplacement. Le déplacement est défini comme la variation de la position d’un objet.
Le Déplacement
Mathématiquement, on défini le déplacement \(\overrightarrow{\Delta x}\) de la manière suivante :
avec:
\(\overrightarrow{x_{f}}\) est la position finale, en [\(m\)]
\(\overrightarrow{x_{0}}\) est la position initiale, en [\(m\)]
\(\overrightarrow{\Delta x}\) est le symbole utilisé pour représenter le déplacement, en [\(m\)]
Le déplacement est un vecteur : il a donc une direction et une norme. On le représente par une flèche qui pointe de la position initiale vers la position finale. Sur la figure Fig. 3.1, on considère par exemple l’enseignante qui se déplace par rapport au tableau. La position initiale de l’enseignante est \(x_{0}=1.5\,m\) et sa position finale est \(x_{f}=3.5\,m\). Son déplacement peut donc s’exprimer ainsi, \(\Delta x=x_{f}-x_{0}=3.5\,m-1.5\,m= +2.0\,m\). Dans ce système de coordonnées, un mouvement vers la droite est positif, alors qu’un mouvement vers la gauche est négatif.
On considère maintenant le passager qui marche dans le référentiel de l’avion sur la Fig. 3.2.
La position initiale du passager de l’avion est \(x_0=6.0\,m\) et sa position finale est \(x_f=2.0\,m\). Donc son déplacement peut s’exprimer ainsi, \(\Delta x=x_{f}-x_{0}=2.0\,m-6.0\,m= -4.0\,m\). Son déplacement est négatif puisqu’il se déplace vers l’arrière de l’avion, c’est à dire dans la direction des \(x\) négatifs dans le système de coordonnées choisi.
Dans les mouvements à une dimension, le sens du déplacement peut être spécifié avec un signe plus (\(+\)) ou un signe moins (\(-\)). Lorsqu’on se lance dans un problème, il faut définir quelle est le sens positif (vers la droite ou vers le haut en général, bien qu’on soit libre de choisir n’importe quelle direction comme étant positive).
Différence entre distance et distance parcourue#
Il est important de faire attention lorsqu’on parle de distance car ce mot a deux sens différents en physique : la distance entre deux points, et la distance parcourue par un objet:
La distance est l’amplitude (la norme) du déplacement direct entre deux positions.
La distance parcourue est la longueur totale du chemin parcouru entre deux positions. Ce n’est pas un vecteur, elle n’a pas de direction et pas non plus de signe négatif.
Par exemple, si l’enseignante fait un aller-retour devant le tableau, sa distance parcourue sera se \(2+2=4\,m\), alors que sa distance est de \(0\,m\) puisqu’elle revient à sa position initiale (\(x_{f}=x_{0}\)).
Fig. 3.3 La distance parcourue (en bleu) peut être plus grande que la distance (en rose) entre deux positions.#
Il est important de comprendre que la distance parcourue par un objet entre deux positions n’est pas forcément égale à la distance entre ces deux positions (amplitude du déplacement). Par exemple, si un objet change de direction lors de son mouvement, la distance totale parcourue sera forcement plus grande que la distance directe entre les deux positions.
Confusions liées à la notion de déplacement#
On oublie souvent que la distance parcourue peut être plus grande que la distance entre deux positions. Cette dernière correspond à l’amplitude du déplacement, la longueur du trajet, sans considérer la direction (juste un nombre avec son unité). Par exemple, l’enseignante pourrait faire des va-et-vient devant le tableau, peut-être \(150\) mètres au total, pour finalement s’arrêter seulement \(2\) mètres à droite de son point de départ. Dans ce cas là, son déplacement serait \(+2.0\,m\), l’amplitude de son déplacement serait \(2.0\,m\), mais la distance parcourue s’élèverait à \(150\,m\). En cinématique, on utilise surtout les notions de déplacement et d’amplitude de déplacement, et très rarement la notion de distance parcourue.
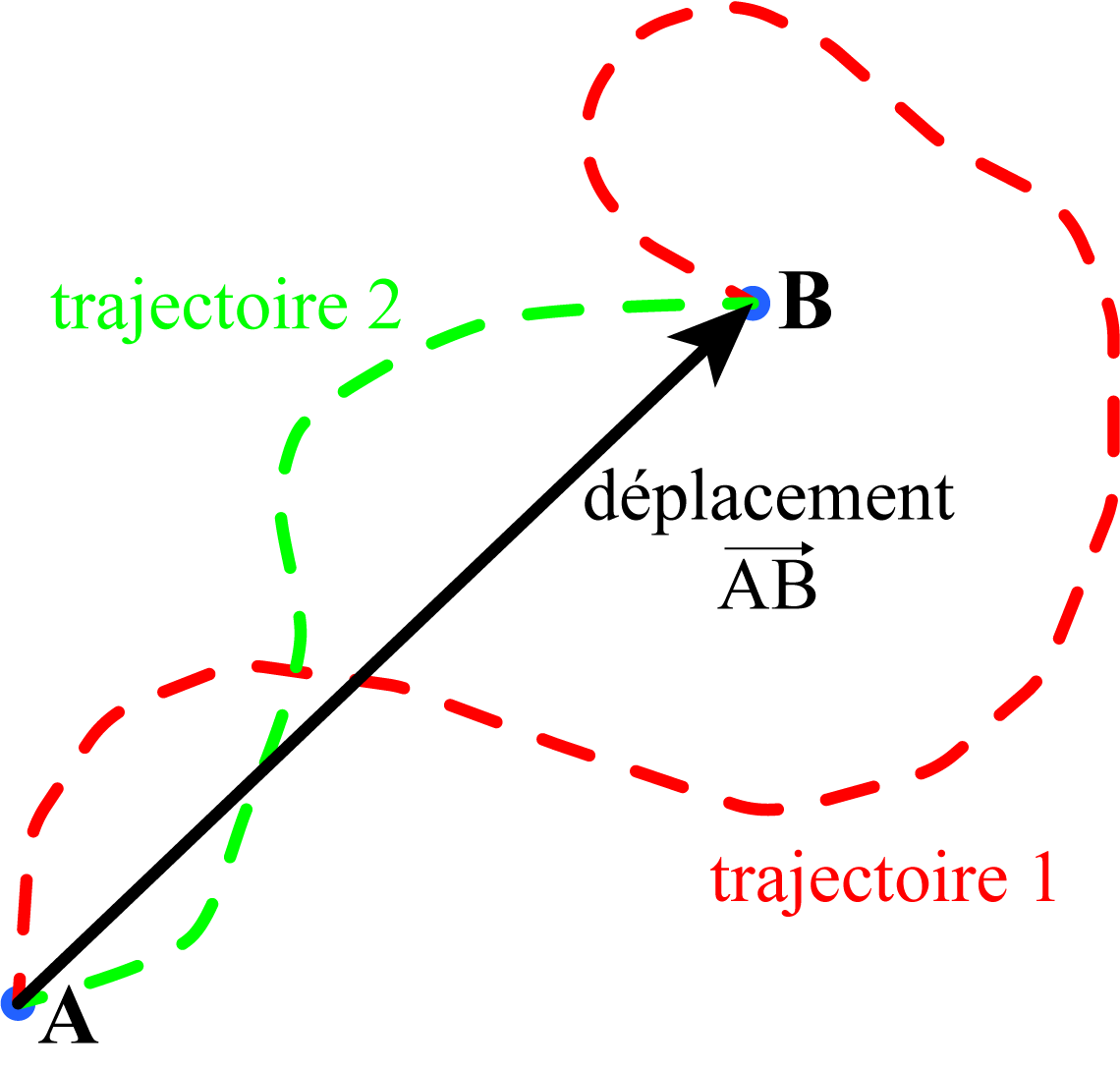
Fig. 3.4 C’est uniquement le déplacement \(\overrightarrow{AB}\) qui sera pris en compte, et non les trajectoires \(1\) et \(2\), pour décrire le déplacement#
Pour bien comprendre cela, on peut marquer les points de départ et d’arrivée du mouvement. Le déplacement est simplement la différence entre les positions des deux marques, peu importe le chemin emprunté. La distance parcourue, elle, est la longueur totale du chemin emprunté.
Attention
On oublie souvent d’inclure si besoin un signe négatif lorsqu’on calcule un déplacement. Cela peut se produire lorsqu’on soustrait accidentellement la position initiale à la position finale au lieu de soustraire la position finale à la position initiale.
Exercice
Le schéma ci-dessus donne les mouvements de quatre objets. Les valeurs de l’axe horizontal sont en mètres.
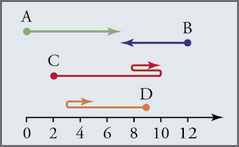
Quel est le déplacement de chaque objet ?
solution
La position initiale de l’objet A était \(0\,m\) et sa position finale est \(7\,m\).
Son déplacement s’exprime ainsi : \(\Delta x_{A}=7\,m-0\,m=+7\,m\).La position initiale de l’objet B était \(12\,m\) et sa position finale est \(7\,m\).
Son déplacement s’exprime ainsi : \(\Delta x_{B}=7\,m-12\,m=-5\,m\).La position initiale de l’objet C était \(2\,m\) et sa position finale est \(10\,m\).
Son déplacement s’exprime ainsi : \(\Delta x_{C}=10\,m-2\,m=+8\,m\).La position initiale de l’objet D était \(9\,m\) et sa position finale est \(5\,m\).
Son déplacement s’exprime ainsi : \(\Delta x_{D}=5\,m-9\,m=-4\,m\).
Exercice
Toujours sur le même schéma. Les valeurs de l’axe horizontal sont en mètres.

Quelle est la distance totale parcourue par chaque objet ?
solution
L’objet A parcourt une distance totale de \(7\,m\).
L’objet B parcourt une distance totale \(5\,m\).
L’objet C parcourt une distance totale de \(8\,m+2\,m+2\,m=12\,m\).
L’objet D parcourt une distance totale de \(6\,m+2\,m=8\,m\).
