Vecteurs et scalaires

Il existe deux types de grandeurs physiques: les scalaires et les vecteurs.

Vecteurs

Quelle est la différence entre une distance de \(20\,km\) et un déplacement de \(20\,km\) vers le Nord ? Alors que la distance n’est définie que par l’amplitude (\(20\,km\)), le déplacement est défini à la fois par l’amplitude et la direction (le Nord). Le déplacement est un exemple de quantité vectorielle. La distance est un exemple de grandeur scalaire. Un vecteur est une quantité avec à la fois une amplitude et une direction. Il existe d’autres grandeurs physique qui sont également des vecteurs comme la vitesse (par exemple \(90\,km/h\) à l’est) ou une force (\(500\,N\) vers le bas).

La direction d’un vecteur à une dimension (unidimensionnel) est donnée par un signe plus (\(+\)) ou moins (\(-\)), par rapport à la direction d’un axe de référence. Les vecteurs sont représentés graphiquement par des flèches. Une flèche utilisée pour représenter un vecteur a une longueur proportionnelle à l’amplitude (valeur) du vecteur (par exemple, plus l’amplitude est grande, plus la longueur du vecteur est importante) et pointe dans la même direction que le vecteur. On écrira les vecteurs avec une lettre surmontée d’une flèche. Par exemple le vecteur déplacement s’écrira \(\vec{x}\).

Les vecteurs ayant surtout un sens pour des mouvements à plusieurs dimension, on peut omettre la flèche sur le \(x\) pour des mouvements à une dimension.

En mécanique, quatre vecteurs seront régulièrement utilisé:

1. Le déplacement \(\vec{d}\)

2. Le vecteur vitesse \(\vec{v}\)

3. Le vecteur accélération \(\vec{a}\)

4. Le vecteur force \(\vec{F}\)

On dessine géométriquement les vecteurs par des flèches; la droite qui supporte la flèche indique la direction, la pointe de la flèche indique le sens et la longueur de flèche indique la valeur.

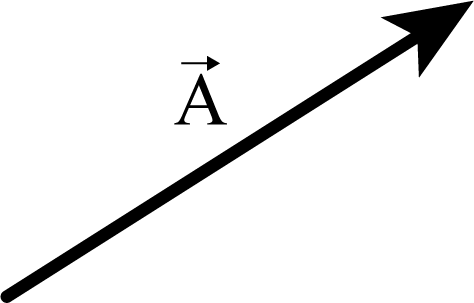
Fig. 1 On dessine géométriquement les vecteurs par des flèches; la droite qui supporte la flèche indique la direction, la pointe de la flèche indique le sens et la longueur de flèche indique la valeur.

Scalaires

Certaines grandeurs physiques, comme la masse, n’ont aucune direction. Un scalaire est une quantité qui a une grandeur, mais aucune direction. Par exemple, la température (\(21.0°C\)), les kilocalories d’énergie d’une barre chocolatée (\(250\,kcal\)), la taille d’une personne (\(1.80\,m\)) et la distance d’un marathon (\(42.195\,km\)) sont tous des scalaires - des quantités sans direction spécifiée. Notez, cependant, qu’un scalaire peut être négatif, comme une température de \(-5.0°C\) ou positif. Dans ce cas, le signe moins indique un point sur une échelle plutôt qu’une direction. Les scalaires ne sont jamais représentés par des flèches.

Quelques autres grandeurs physique scalaires que nous utiliserons régulièrement:

1. Le temps et la durée sont des grandeurs scalaires: \(t = 11\,h\,45\) et \(\Delta t = 0,034\,s\) sont des indications suffisantes.

2. La masse est une grandeur scalaire: \(m = 48\,kg\).

3. Le volume et la surface sont des scalaires: \(V = 12\,m^{3}\) ; \(S = 23\,cm^{2}\).

Multiplication d’un vecteur par un scalaire

Multiplier, ou diviser un vecteur par un scalaire consiste à modifier la norme de ce vecteur sans changer sa direction. Géométriquement, il s’agit d’une homothétie (un zoom).

Le vecteur \(\vec{a}\) peut être multiplié par un scalaire \(m\), pour donner un nouveau vecteur \(\vec{b}=m\cdot \vec{a}\).

Si \(m\) est négatif, le sens de \(\vec{b}\) sera opposé à celui de \(\vec{a}\).

La Fig. 2 illustre la multiplication du vecteur \(\vec{a}\) par 0,5 et par -2.

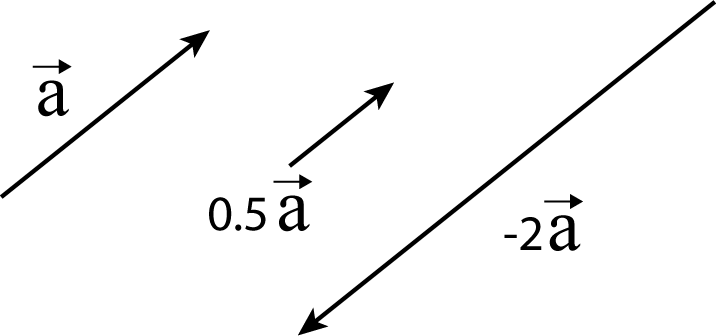
Fig. 2 Multiplication d’un vecteur par un scalaire

Addition de vecteurs

Supposons qu’un objet se déplace du point A vers B, puis de B vers C. On peut représenter le déplacement total par deux vecteurs déplacements successifs, les vecteurs \(\overrightarrow{AB}\) et \(\overrightarrow{BC}\). Le déplacement résultant de ces deux déplacements est un seul déplacement, soit celui allant de A vers C. On appelle \(\overrightarrow{AC}\) la somme vectorielle (ou résultante) des vecteurs \(\overrightarrow{AB}\) et \(\overrightarrow{BC}\).

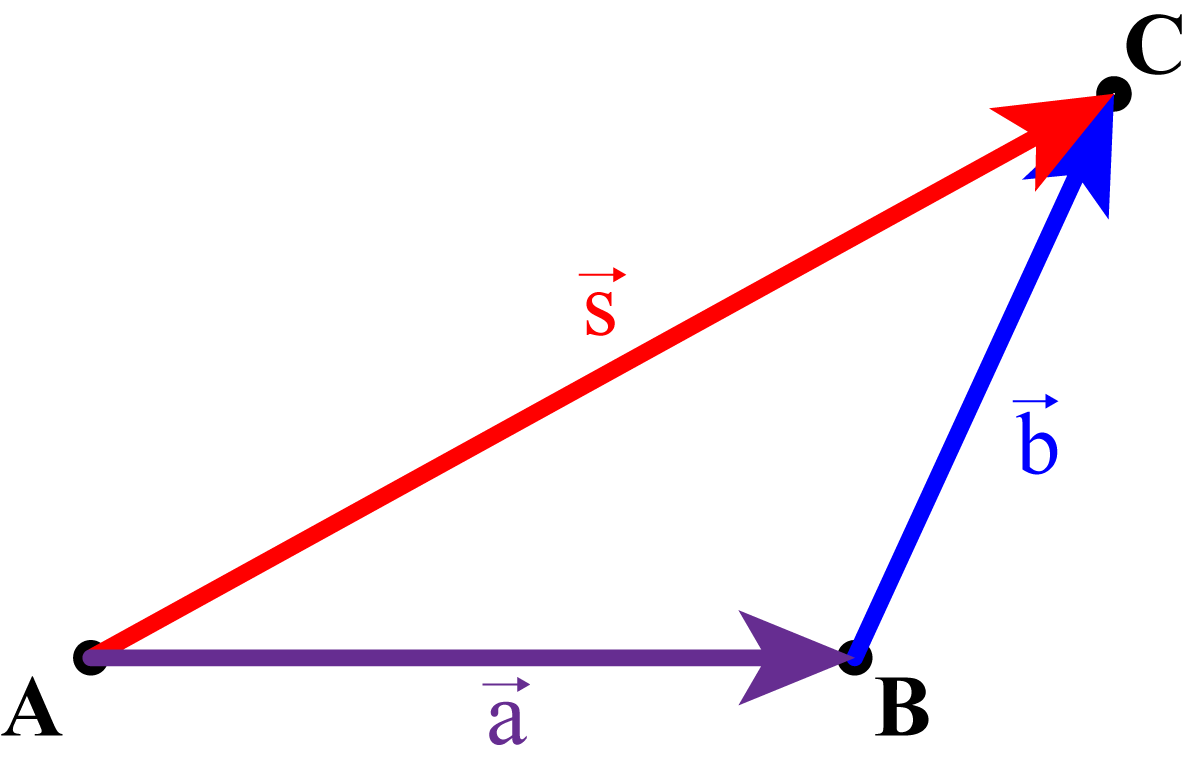
Fig. 3 \(\overrightarrow{AC}=\vec{s}\) est la somme vectorielle des vecteurs \(\overrightarrow{AB}=\vec{a}\) et \(\overrightarrow{BC}=\vec{b}\)

Cette somme vectorielle n’est pas une somme algébrique ordinaire car elle prend en compte non seulement la valeur du vecteur mais surtout sa direction.

Astuce

Afin d’alléger la notation, on représentera le vecteur déplacement, de A à B, \(\overrightarrow{AB}\) par une seule lettre. On écrira par exemple \(\overrightarrow{AB}=\vec{a}\).

Le déplacement opposé de B à A sera noté \(\overrightarrow{BA}\) avec la propriété suivante :

\[\overrightarrow{BA}=-\overrightarrow{AB}=-\vec{a}\]

Avec cette notation, on peut représenter la relation entre les trois vecteurs de la Fig. 3 par l’équation vectorielle suivante :

\[\vec{s}=\vec{a}+\vec{b}\]

L’addition vectorielle présente une propriété similaire à l’addition scalaire; l’ordre des vecteurs à additionner n’a pas d’importance. Ainsi additionner \(\vec{a}\) à \(\vec{b}\) donne le même résultat qu’additionner \(\vec{b}\) à \(\vec{a}\) :

\[\vec{a}+\vec{b}=\vec{b}+\vec{a}\]

Addition géométrique

La somme de deux vecteurs s’obtient graphiquement par la méthode des parallélogrammes comme illustré ci-dessous.

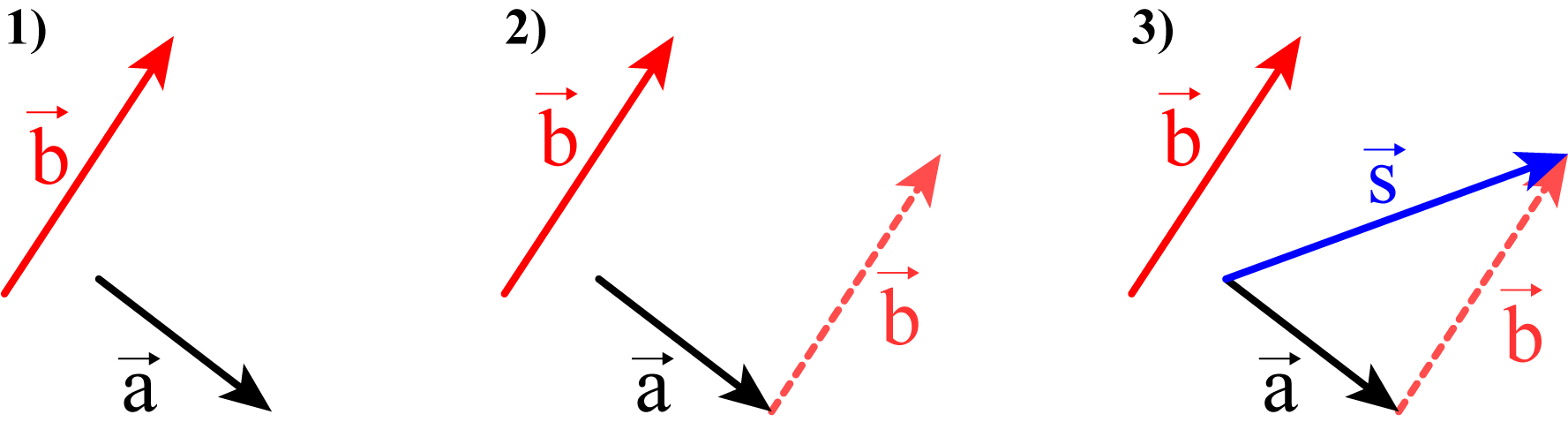
Fig. 4 Addition géométrique de deux vecteurs. 1) On cherche à additionner \(\vec{a}\) et \(\vec{b}\). 2) On fait une translation de \(\vec{b}\) jusqu’à l’extrémité de \(\vec{a}\). 3) On relie l’origine de \(\vec{a}\) à l’extrémité de \(\vec{b}\)

La construction géométrique \(\vec{a}+\vec{b}\), illustrée à la Fig. 4, consiste à faire glisser le vecteur \(\vec{b}\), sans en modifier ni l’intensité, ni le sens, et de faire coïncider son origine avec l’extrémité du vecteur \(\vec{a}\). Le vecteur résultant \(\vec{s}=\vec{a}+\vec{b}\) a pour origine celle du vecteur \(\vec{a}\) et pour extrémité celle du vecteur \(\vec{b}\).

Addition algébrique

L’addition algébrique de deux vecteurs s’obtient en additionnant les coordonnées de chaque vecteurs. Pour cela, il faut d’abord décomposer les vecteurs selon un système d’axes.

Notations

On prendra l’habitude d’écrire un vecteur avec ses coordonnées notées en ligne ou en colonne :

\[\begin{split}\vec{a}=(a_{x};a_{y})=\begin{pmatrix} a_{x} \\ a_{y} \end{pmatrix}\end{split}\]

Décomposition d’un vecteur

Pour pouvoir additionner algébriquement deux vecteurs \(\vec{a}\) et \(\vec{b}\), il faut impérativement placer un référentielle à 2 ou 3 dimensions (un vecteur à une dimension est un scalaire!). Dans le cadre de ce cours, on se limitera à un système d’axes à 2 dimensions.
Une fois le système d’axes \(0xy\) placé, le vecteur oblique \(\vec{a}\) ou \(\vec{b}\) peut se décomposer en deux vecteurs qui sont les composantes horizontale et verticale du vecteur.

Le vecteur oblique \(\vec{a}\) se décompose ainsi en un vecteur \(\vec{a_{x}}\) et un vecteur \(\vec{a_{y}}\).

\[\begin{split}\vec{a}=\vec{a_{x}}+\vec{a_{y}}=\begin{pmatrix} a_{x} \\ 0 \end{pmatrix}+\begin{pmatrix} 0 \\ a_{y} \end{pmatrix}=\begin{pmatrix} a_{x} \\ a_{y} \end{pmatrix}\end{split}\]

La décomposition d’un vecteur consiste à trouver les coordonnées de ce vecteur dans le système d’axes proposé.

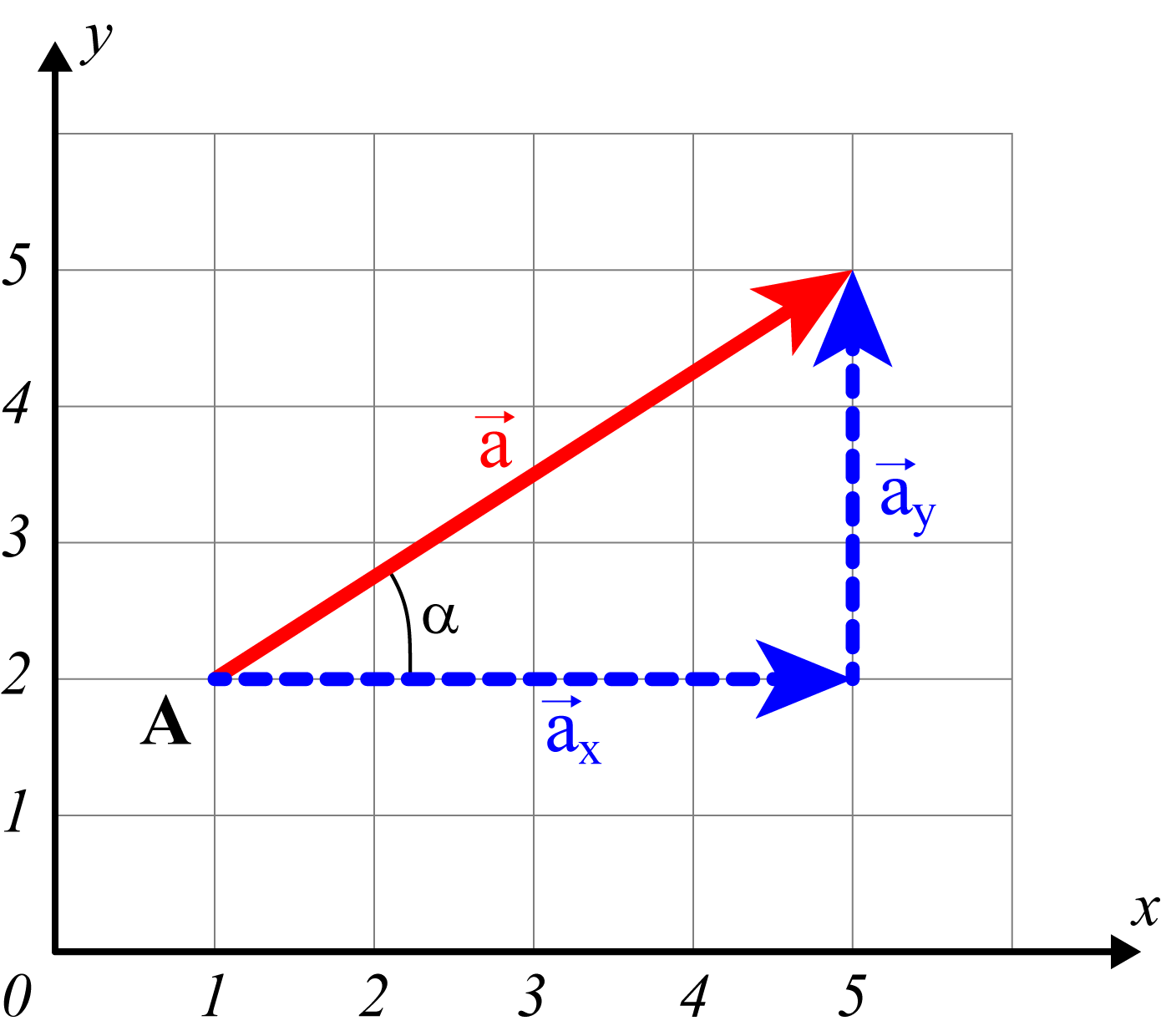
Fig. 5 Décomposition du vecteur \(\vec{a}\) selon ses composantes horizontale \(\vec{a_{x}}\) et verticale \(\vec{a_{y}}\)

La norme, notée \(\Vert\vec{a}\Vert\) (ou simplement \(a\)), de \(\vec{a}\) se calcul grâce au théorème de Pythagore :

\[\Vert \vec{a}\Vert=a=\sqrt{a_{x}^{2}+a_{y}^{2}}\]

Les coordonnées \(a_{x}\) et \(a_{y}\) de \(\vec{a}\) de la Fig. 5 peuvent être trouvées grâce à la trigonométrie :

\[\begin{split}\begin{align*} \overrightarrow{a_{x}}=\begin{pmatrix} a_{x} \\ 0 \end{pmatrix} & =\begin{pmatrix} a\cdot\cos\alpha \\ 0 \end{pmatrix}\\ \\ \overrightarrow{a_{y}}=\begin{pmatrix} 0 \\ a_{y} \end{pmatrix} & =\begin{pmatrix} 0 \\ a\cdot\sin\alpha \end{pmatrix} \end{align*}\end{split}\]

L’addition de deux vecteurs \(\vec{a}\) et \(\vec{b}\), s’obtient en additionnant chacune des coordonnées horizontale et verticale de \(\vec{a}\) et \(\vec{b}\) :

\[\begin{split}\vec{a}+\vec{b}=\begin{pmatrix} a_{x} \\ a_{y} \end{pmatrix}+\begin{pmatrix} b_{x} \\ b_{y} \end{pmatrix}=\begin{pmatrix} a_{x}+b_{x} \\ a_{y}+b_{y} \end{pmatrix}=\begin{pmatrix} s_{x} \\ s_{y} \end{pmatrix}=\vec{s}\end{split}\]

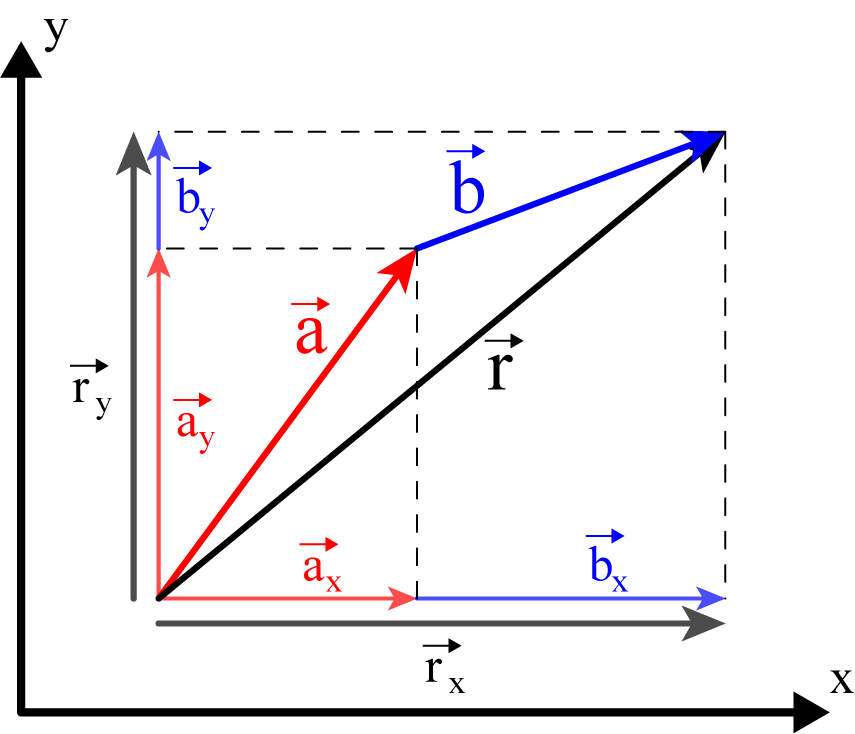
Fig. 6 Les composantes du vecteur \(\vec{s}\) résultant correspondent à la somme des composantes des vecteurs \(\vec{a}\) et \(\vec{b}\); soit \(\vec{s_{x}}=\vec{a_{x}}+\vec{b_{x}}\) et \(\vec{s_{y}}=\vec{a_{y}}+\vec{b_{y}}\)

Exemple

Sur la Fig. 5 :

1. Quelles sont les composantes \(\vec{a_{x}}\) et \(\vec{a_{y}}\) du vecteur \(\vec{a}\) ?

2. Calculer la norme \(\Vert\vec{a}\Vert\) et l’angle \(\alpha\) du vecteur \(\vec{a}\) ?

solution

Selon la Fig. 5, on peut écrire \(\vec{a_{x}}=\begin{pmatrix} 4 \\ 0 \end{pmatrix}\) et \(\vec{a_{y}}=\begin{pmatrix} 0 \\ 3 \end{pmatrix}\)

Le vecteur \(\vec{a}\) vaut donc : \(\vec{a}=\vec{a_{x}}+\vec{a_{y}}=\begin{pmatrix} 4 \\ 0 \end{pmatrix}+\begin{pmatrix} 0 \\ 3 \end{pmatrix}=\begin{pmatrix} 4 \\ 3 \end{pmatrix}\).

La norme de \(\vec{a}\) se calcul par Pythagore : \(\Vert\vec{a}\Vert=a=\sqrt{4^{2}+3^{2}}=5\)

L’angle \(\alpha\), qui est donné par \(\tan\alpha=\frac{a_{y}}{a_{x}}\), mesure \(36,87°\). Ce qui nous donne bien :

\[\begin{split}a_{x}=a\cdot \cos\alpha=5\cdot\cos 36,87°=4\\ a_{y}=a\cdot \sin\alpha=5\cdot\sin 36,87°=3\end{split}\]

PhET simulation

Addition de vecteurs