6.3. Démonstration des équations de la cinématique#
Rappel des équations#
Les quatre équations de la cinématique :
1ère équation cinématique : \(v(t)=a\cdot t+v_{0}\)#
Cette équation cinématique est probablement la plus simple à démontrer puisqu’il s’agit seulement d’une version réarrangée de la définition de l’accélération. On part donc de la définition de l’accélération :
On en déduit l’expression de \(v\) :
2ème équation cinématique : \(\Delta x=\frac{v(t)+v_{0}}{2}\cdot t\)#
Une manière simple de démontrer la deuxième équation cinématique est de partir de la représentation graphique de la vitesse d’un objet subissant une accélération constante - c’est à dire, avec une pente constante - et ayant une vitesse initiale \(v_{0}\) comme illustrée ci-dessous.
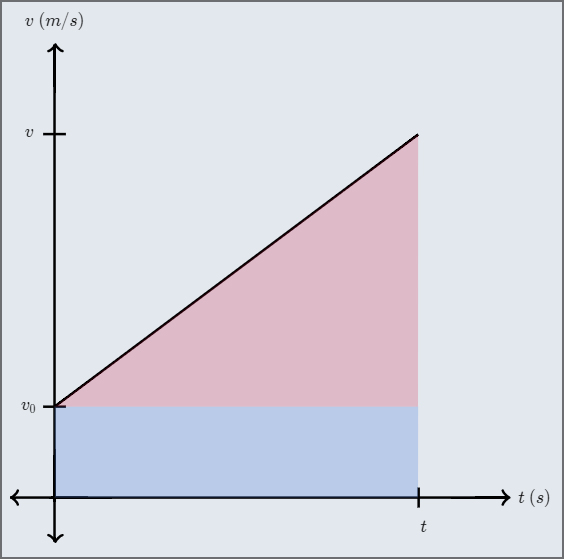
Fig. 6.1 L’aire sous la courbe de \(v(t)\) correspond au déplacement \(\Delta x\)#
L’aire sous cette courbe de \(v(t)\) donne le déplacement \(\Delta x\) de l’objet.
Pour que l’aire soit plus simple à calculer, on la décompose en un rectangle bleu et un triangle rouge comme le montre la Fig. 6.1.
La hauteur du rectangle bleu est \(v_{0}\) et sa largeur est \(t\), son aire est donc \(v_{0}\cdot t\).
La base du triangle rouge est \(t\) et sa hauteur est \(v(t)-v_{0}\), son aire est donc \(\dfrac{1}{2}(v(t)-v_{0})\cdot t\).
L’aire totale est la somme des aires du rectangle bleu et du triangle rouge.
En distribuant le facteur \(\dfrac{1}{2}t\) on obtient :
On en déduit la deuxième équation cinématique :
Cette formule est intéressante car si l’on divise les deux côtés par \(t\), on obtient \(\frac{\Delta x}{t}=\frac{v(t)+v_{0}}{2}\). Cela montre que la moyenne des vitesses finale et initiale \(\frac{v(t)+v_{0}}{2}\), est égale à la vitesse moyenne \(\frac{\Delta x}{t}\). Cela est vrai uniquement lorsque l’accélération est constante puisque cette formule a été démontrée en partant d’une courbe de \(v(t)\) de pente constante.
3ème équation cinématique : \(\Delta x=\frac{1}{2}a\cdot t^{2}+v_{0}\cdot t\)#
Il y a différentes manières de démontrer l’équation \(\Delta x=\frac{1}{2}a\cdot t^{2}+v_{0}\cdot t\) : une démonstration géométrique assez visuelle et une démonstration analytique plus calculatoire. Voici uniquement la démonstration géométrique.
Un objet, ayant une vitesse initiale \(v_{0}\), est soumis à une accélération constante de manière à atteindre la vitesse finale \(v\).

Fig. 6.2 L’aire sous la courbe de \(v(t)\) correspond au déplacement \(\Delta x\)#
Puisque l’aire sous la courbe de \(v(t)\) donne le déplacement \(\Delta x\), on peut affirmer que, à chaque terme de droite dans l’équation \(\Delta x=\dfrac{1}{2}a\cdot t^{2}+v_{0}\cdot t\), est associé une aire sur la représentation graphique de la figure Fig. 6.2.
Le terme \(v_{0}\cdot t\) représente l’aire du rectangle bleu puisque \(A_{rectangle}=hauteur\cdot largeur\)
Le terme \(\frac{1}{2}a\cdot t^{2}\) représente l’aire du triangle rouge puisque \(A_{triangle}=\frac{1}{2}\cdot base\cdot hauteur=\frac{1}{2}t\cdot (v-v_{0})=\frac{1}{2}\Delta v\cdot t\) avec \(\Delta v=a\cdot t\)
En se rappelant que l’aire totale sous la courbe donne le déplacement, on retrouve la formule \(\Delta x=\frac{1}{2}a\cdot t^{2}+v_{0}\cdot t\). Il est important de remarquer que cette équation - comme les autres équations cinématiques - n’est valable que lorsque l’accélération est constante, c’est à dire lorsque la courbe de \(v(t\)) est une droite.
La troisième équation cinématique peut être démontrée analytiquement en incorporant la première équation, \(v=a\cdot t+v_{0}\), dans la seconde, \(\frac{\Delta x}{t}=\frac{v+v_{0}}{2}\).
4ème équation cinématique : \(v(t)^{2}-v_{0}^{2}=2a\cdot\Delta x\)#
La quatrième équation cinématique est très utile quand on ne connaît pas le temps \(t\). Pour démontrer cette quatrième équation, on part de la deuxième: \(\Delta x=\dfrac{v(t)+v_{0}}{2}\cdot t\)
L’objectif est d’éliminer \(t\) de cette formule. Pour ce faire, on réécrit la première équation cinématique, \(v(t)=a\cdot t+v_{0}\), sous la forme \(t=\frac{v(t)-v_{0}}{a}\). On utilise ensuite cette expression pour remplacer \(t\) dans la deuxième équation cinématique :
On développe la partie droite de l’équation :
Et on obtient la quatrième équation cinématique :
