9.8. Les autres forces

Poids et force normale, tension et autres forces

Les forces reçoivent de nombreux noms, tels que la poussée, la traction, la poussée, la portance, le poids, la friction et la tension. Traditionnellement, les forces ont été regroupées en plusieurs catégories et ont reçu des noms en fonction de leur source, de leur mode de transmission ou de leurs effets. Les plus importantes de ces catégories sont abordées dans cette section, ainsi que quelques applications intéressantes. D’autres exemples de forces sont discutés plus loin dans ce texte.

Poids \(\vec{P}\) et Force normale \(\vec{N}\)

Le poids (également appelé force de gravité) est une force omniprésente qui agit à tout moment et doit être contrecarrée pour empêcher un objet de tomber. Vous remarquerez certainement que vous devez supporter le poids d’un objet lourd en poussant dessus lorsque vous le maintenez immobile, comme illustré à la Fig. 9.10(a). Mais comment des objets inanimés comme une table supportent-ils le poids d’une masse placée dessus, comme le montre la Fig. 9.10(b)? Lorsque le sac de nourriture pour chien est placé sur la table, la table s’affaisse légèrement sous la charge. Cela serait perceptible si la charge était placée sur une table à cartes, mais même les objets rigides se déforment lorsqu’une force leur est appliquée. À moins que l’objet ne soit déformé au-delà de sa limite, il exercera une force de rappel semblable à un ressort déformé (ou un trampoline ou un plongeoir). Plus la déformation est importante, plus la force de rappel est grande. Ainsi, lorsque la charge est placée sur la table, la table s’affaisse jusqu’à ce que la force de rappel devienne aussi grande que le poids de la charge. À ce stade, la force externe résultante sur la charge est nulle. Telle est la situation lorsque la charge est stationnaire sur la table. La table s’affaisse rapidement et l’affaissement est léger donc on ne le remarque pas. Mais c’est similaire à l’affaissement d’un trampoline lorsque vous montez dessus.

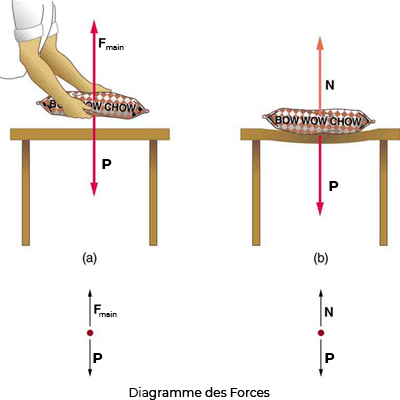
Fig. 9.10 (a) La personne qui tient le sac de nourriture pour chien doit fournir une force ascendante \(\vec{F}_{main}\) égale en magnitude et dans le sens opposé au poids de l’aliment \(\vec{P}\). (b) La table s’affaisse lorsque la nourriture pour chien est placée dessus, un peu comme un trampoline rigide. Les forces de rappel élastiques dans la table augmentent à mesure qu’elle s’affaisse jusqu’à ce qu’elles fournissent une force \(\vec{N}\) égale en amplitude et dans la direction opposée au poids de la charge.

Nous devons conclure que tout ce qui supporte une charge, qu’elle soit animée ou non, doit fournir une force ascendante égale au poids de la charge, comme nous l’avons supposé dans quelques-uns des exemples précédents. Si la force supportant une charge est perpendiculaire à la surface de contact entre la charge et son support, cette force est définie comme étant une force normale et on donne ici le symbole \(\vec{N}\). (Ce n’est pas l’unité de la force \(N\).) Le mot normal signifie perpendiculaire à une surface. La force normale peut être inférieure au poids de l’objet si l’objet est sur une pente, comme vous le verrez dans l’exemple suivant.

Idées fausse commune: Force normale (\(\vec{N}\)) et Unité de force (\(N\))

Dans cette section, nous avons introduit la quantité de force normale, qui est représentée par la variable \(\vec{N}\). Cela ne doit pas être confondu avec le symbole du newton, qui est également représenté par la lettre \(N\). Ces symboles sont particulièrement importants à distinguer car les unités d’une force normale (\(\vec{N}\)) se trouvent être des newtons (\(N\)). Par exemple, la force normale \(\vec{N}\) que le sol exerce sur une chaise pourrait être \(\vec{N}=100\,N\). Une différence importante est que la force normale est un vecteur, tandis que le newton est simplement une unité. Pour éviter cette confusion on utilisera quelques fois la lettre \(\vec{S}\) pour représenter cette force normale (\(\vec{S}\) pour Soutiens). Attention à ne pas confondre ces lettres dans vos calculs !
Vous rencontrerez plus de similitudes entre les variables et les unités au fur et à mesure que vous progresserez en physique. Un autre exemple de ceci est la quantité de travail (\(w\)) et l’unité watts (\(W\)).

Exemple : Le poids sur une pente, un problème à deux dimensions

Considérez le skieur sur une pente illustrée à la figure ci-dessous. Sa masse, équipement compris, est de \(60,0\,kg\).

1. Quelle est son accélération si le frottement est négligeable ?

2. Quelle est son accélération si l’on sait que le frottement est de \(45,0\,N\) ?

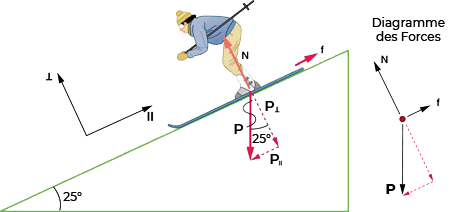
Fig. 9.11 Puisque le mouvement et le frottement sont parallèles à la pente, il est plus pratique de projeter toutes les forces sur un système de coordonnées où un axe est parallèle à la pente et l’autre est perpendiculaire (axes représentés à gauche du skieur). \(\vec{N}\) est perpendiculaire à la pente et \(\vec{f}\) est parallèle à la pente, mais \(\vec{P}\) a des composants le long des deux axes, à savoir \(P_{\parallel}\) et \(P_{\perp}\). \(\vec{N}\) est égal en grandeur à \(P_{\perp}\), de sorte qu’il n’y ait pas de mouvement perpendiculaire à la pente, mais \(\vec{f}\) est inférieur à \(P_{\parallel}\), de sorte qu’il y ait une accélération de la pente descendante (le long de l’axe parallèle). (crédit : openstax.org)

stratégie

Il s’agit d’un problème à deux dimensions, car les forces sur le skieur (le système d’intérêt) ne sont pas parallèles. L’approche que nous avons utilisée en cinématique bidimensionnelle fonctionne également très bien ici.

Choisissez un système de coordonnées pratique et projeter les vecteurs sur ses axes, créant deux connectés un problème de dimension à résoudre. Le système de coordonnées le plus pratique pour le mouvement sur une pente est celui qui a une coordonnée parallèle à la pente et une perpendiculaire à la pente. (N’oubliez pas que les mouvements le long d’axes perpendiculaires les uns aux autres sont indépendants.) Nous utilisons les symboles \(\perp\) et \(\parallel\) pour représenter respectivement perpendiculaire et parallèle. Ce choix d’axes simplifie ce type de problème, car il n’y a pas de mouvement perpendiculaire à la pente et parce que le frottement est toujours parallèle à la surface entre deux objets.

Les seules forces externes agissant sur le système sont le poids du skieur, le frottement et le support de la pente, respectivement étiquetés \(\vec{P}\), \(\vec{f}\), et \(\vec{N}\) dans la figure ci-dessus. \(\vec{N}\) est toujours perpendiculaire à la pente, et \(\vec{f}\) toujours parallèle. Mais \(\vec{P}\) n’est pas dans la direction de l’un ou l’autre des axes, et donc la première étape que nous prenons est de le projeter en composants le long des axes choisis, en définissant \(P_{\parallel}\) être la composante du poids parallèle à la pente et \(P_{\perp}\) la composante du poids perpendiculaire à la pente.

Une fois cela fait, nous pouvons considérer les deux problèmes distincts de forces parallèles à la pente et de forces perpendiculaires à la pente.

solution

L’amplitude de la composante du poids parallèle à la pente est

\[P_{\parallel}=P\cdot \sin 25°=mg\cdot \sin 25°\]

et la grandeur de la composante du poids perpendiculaire à la pente est

\[P_{\perp}=P\cdot \cos 25°=mg\cdot \cos 25°\]

Solution 1.

Si on néglige la friction. Puisque l’accélération est parallèle à la pente, il suffit de considérer les forces parallèles à la pente. (Les forces perpendiculaires à la pente s’ajoutent à zéro, car il n’y a pas d’accélération dans cette direction.) Les forces parallèles à la pente sont la quantité de poids du skieur parallèle à la pente (\(P_{\parallel}\)) et frottement \(\vec{f}\). En utilisant la deuxième loi de Newton, avec des indices pour désigner des quantités parallèles à la pente,

\[a_{\parallel}=\dfrac{F_{res,\parallel}}{m}\]

où \(F_{res\,\parallel}=P_{\parallel}=mg\sin 25°\), en supposant aucun frottement pour cette partie, de sorte que

\[a_{\parallel}=\dfrac{F_{res\,\parallel}}{m}=\dfrac{mg\cdot\sin 25°}{m}=g\cdot\sin 25°=9,80\,m/s^{2}\cdot 0,4226=4,14\,m/s^{2}\]

est l’accélération.

Solution 2.

En tenant compte du frottement. Nous avons maintenant une valeur donnée du frottement, et nous savons que sa direction est parallèle à la pente et qu’elle s’oppose au mouvement entre les surfaces en contact. Donc la force extérieure résultante est maintenant

\[F_{res\,\parallel}=P_{\parallel}-f\]

et en le substituant à la seconde loi de Newton \(a_{\parallel}=\dfrac{F_{res\,\parallel}}{m}\), donne

\[a_{\parallel}=\dfrac{F_{res\,\parallel}}{m}=\dfrac{P_{\parallel}-f}{m}=\dfrac{mg\sin 25°-f}{m}\]

Nous substituons des valeurs connues pour obtenir

\[a_{\parallel}=\dfrac{(60\,kg\cdot 9,80\,m/s^{2}\cdot 0,4226)-45,0\,N}{60,0\,kg}=3,39\,m/s^{2}\]

qui est l’accélération parallèle à l’inclinaison lorsqu’il y a 45,0 N de friction opposée.

discussion

Comme le frottement s’oppose toujours au mouvement entre les surfaces, l’accélération est plus faible lorsqu’il y a frottement que lorsqu’il n’y en a pas. En fait, il en résulte généralement que si le frottement sur une pente est négligeable, alors l’accélération vers le bas de la pente est \(a=g\cdot \sin\theta\), quelle que soit la masse. Ceci est lié au fait discuté précédemment que tous les objets tombent avec la même accélération en l’absence de résistance de l’air. De même, tous les objets, quelle que soit leur masse, glissent sur une pente sans frottement avec la même accélération (si l’angle est le même).

Décomposition du poids en composantes

Un objet repose sur une pente qui fait un angle \(\theta\) avec l’horizontale.

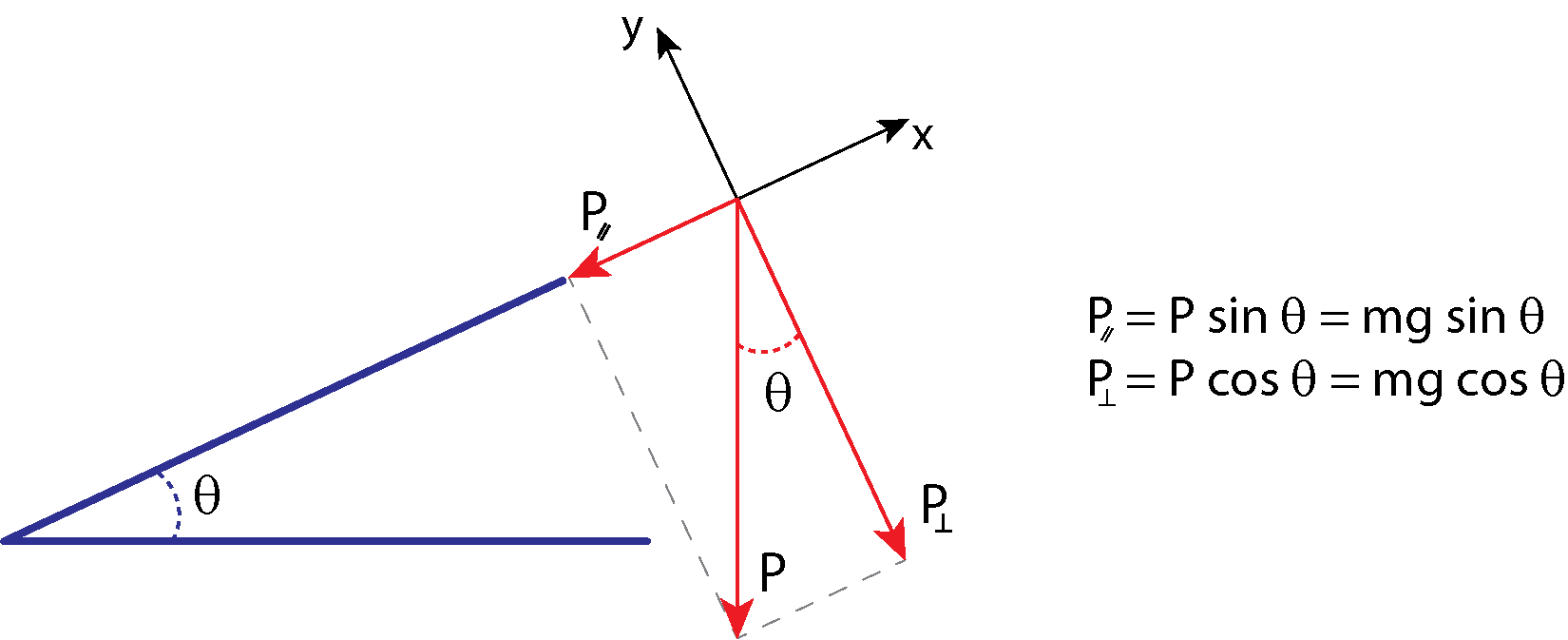
Lorsqu’un objet repose sur une pente qui fait un angle \(\theta\) avec l’horizontale, la force de gravité agissant sur l’objet est divisée en deux composantes: une force agissant perpendiculairement au plan (\(P_{\perp}\)), et une force agissant parallèlement au plan (\(P_{\parallel}\)). La force perpendiculaire du poids (\(P_{\perp}\)) est généralement égale en amplitude et dans la direction opposée à la force normale, \(\vec{N}\). La force agissant parallèlement au plan (\(P_{\parallel}\)) provoque l’accélération de l’objet sur la pente. La force de friction, \(\vec{f}\), s’oppose au mouvement de l’objet, il agit donc vers le haut le long du plan.

Il est important d’être prudent lors de la résolution du poids de l’objet en composants. Si l’angle de l’inclinaison est à un angle \(\theta\) à l’horizontale, alors les grandeurs des composantes de poids sont:

\[P_{\parallel}=P\cdot \sin\theta=mg\cdot \sin\theta\]

et

\[P_{\perp}=P\cdot \cos\theta=mg\cdot \cos\theta\]

Au lieu de mémoriser ces équations, il est utile de pouvoir les retrouver à partir quelques connaissance de base. Pour ce faire, dessinez le triangle rectangle formé par les trois vecteurs de poids. Notez que l’angle \(\theta\) de l’inclinaison est le même que l’angle formé entre \(\vec{P}\) et \(\vec{P}_{\perp}\). Connaissant cette propriété, vous pouvez utiliser la trigonométrie pour déterminer l’amplitude des composantes du poids :

\[\begin{split}\begin{align*} \cos\theta = \dfrac{P_{\perp}}{P}\,\, & \Rightarrow\,\,P_{\perp}=P\cos\theta=mg\cos\theta\\ \sin\theta = \dfrac{P_{\parallel}}{P}\,\, & \Rightarrow\,\,P_{\parallel}= P\sin\theta=mg\sin\theta \end{align*}\end{split}\]

Tension \(\vec{T}\)

Une tension est une force sur qui agit sur la longueur d’un support, tel qu’une corde ou un câble. Le mot tension vient d’un mot latin signifiant étirer. Pas par coïncidence, les cordons flexibles qui transportent les forces musculaires vers d’autres parties du corps sont appelés tendons. Tout connecteur flexible, tel qu’une ficelle, une corde, une chaîne, un fil ou un câble, ne peut exercer de traction que parallèlement à sa longueur; ainsi, une force appliquée par l’un de ces objets crée une tension avec une direction parallèle l’objet (le long de l’objet). Il est important de comprendre que la tension est toujours une force de traction; considérez la phrase: Vous ne pouvez pas pousser une corde. La force de tension tire vers l’extérieur le long des deux extrémités d’une corde.

Prenons l’exemple d’une personne tenant une masse sur une corde comme le montre la Fig. 9.12.

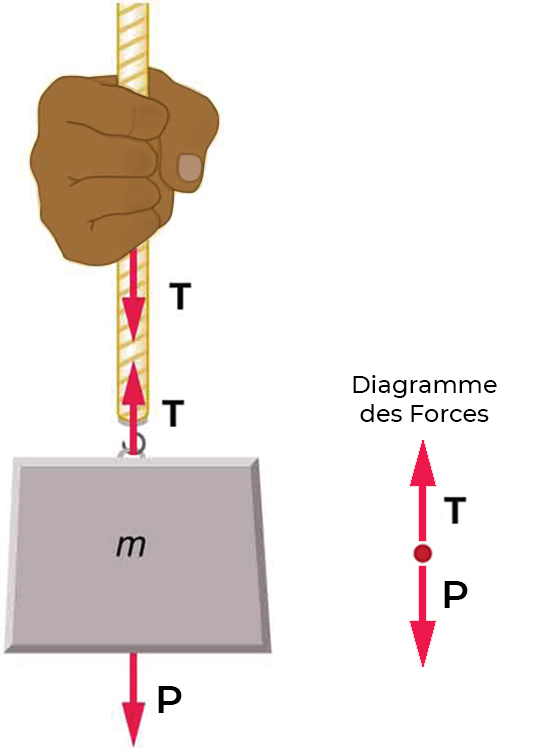
Fig. 9.12 Lorsqu’un connecteur parfaitement flexible (qui ne nécessite aucune force pour le plier) tel que cette corde transmet une force \(\vec{T}\), cette force doit être parallèle à la longueur du câble, comme illustré. La traction exercée par un tel connecteur flexible est une tension. Notez que la corde tire avec une force égale mais dans des sens opposés sur la main et la masse supportée (en négligeant le poids de la corde). Ceci est un exemple de la troisième loi de Newton. La corde est le support qui transporte les forces égales et opposées entre les deux objets. La tension n’importe où dans la corde entre la main et la masse est égale. Une fois que vous avez déterminé la tension à un endroit, vous avez déterminé la tension à tous les endroits le long de la corde.

La tension dans la corde doit être égale au poids de la masse supportée, comme nous pouvons le prouver en utilisant la deuxième loi de Newton. Si la masse de \(5,00\,kg\) sur la figure est stationnaire, alors son accélération est nulle, et donc \(\vec{F}_{res}=0\). Les seules forces externes agissant sur la masse sont son poids \(\vec{P}\) et la tension \(\vec{T}\) fournie par la corde. Donc,

\[F_{res}=\Sigma F=T-P=0\]

où \(T\) et \(P\) sont les amplitudes de la tension et du poids et leurs signes indiquent la direction, le haut étant ici positif. Ainsi, comme vous vous en doutez, la tension est égale au poids de la masse supportée:

\[T=P=mg\]

Pour une masse de \(5.00\,kg\), alors (en négligeant la masse de la corde) on voit que

\[T=mg=5.0\,kg\cdot 9.81\,m/s^{2}=49.1\,N\]

Si nous coupons la corde et insérons un ressort, le ressort s’étendrait sur une longueur correspondant à une force de \(49.1\,N\), fournissant une observation directe et une mesure de la force de tension dans la corde.

Les connecteurs flexibles sont souvent utilisés pour transmettre des forces dans les coins, comme dans un système de traction d’hôpital, une articulation à doigt ou un câble de frein de vélo. S’il n’y a pas de frottement, la tension est transmise sans diminution. Seule sa direction change et il est toujours parallèle au connecteur flexible. Ceci est illustré à la Fig. 9.13.

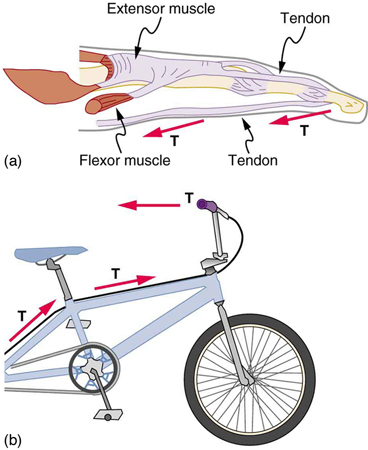
Fig. 9.13 (a) Tendons dans la force de transport du doigt \(\vec{T}\) des muscles à d’autres parties du doigt, en changeant généralement la direction de la force, mais pas son ampleur (les tendons sont relativement sans frottement). (b) Le câble de frein d’une bicyclette porte la tension \(\vec{T}\) du guidon au mécanisme de frein. Encore une fois, la direction mais pas l’amplitude de \(\vec{T}\) est changée. (crédit : openstax.org)

Exemple : Quelle est la tension dans une corde tendue ?

Calculez la tension du câble supportant le funambule de \(70.0\,kg\) illustré à la figure ci-dessous.

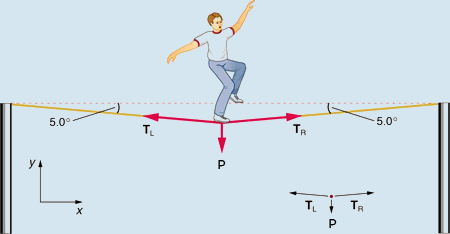
Fig. 9.14 Le poids d’un funambule fait fléchir un fil de 5.0 degrés. Le système qui nous intéresse ici est le point du fil où se tient le funambule.

stratégie

Comme vous pouvez le voir sur la figure, le fil n’est pas parfaitement horizontal (il ne peut pas l’être!), Mais plié sous le poids (\(\vec{P}\)) de la personne. Ainsi, la tension de part et d’autre de la personne a une composante ascendante qui peut supporter son poids.

Comme d’habitude, les forces sont des vecteurs représentés graphiquement par des flèches ayant les mêmes directions que les forces et des longueurs proportionnelles à leurs grandeurs. Le système est le funambule, et les seules forces externes agissant sur lui sont son poids \(\vec{T}\) et les deux tensions \(\vec{T}_{L}\) (tension gauche) et \(\vec{T}_{R}\) (tension droite), comme illustré. Il est raisonnable de négliger le poids du fil lui-même.

La force externe résultante est nulle puisque le système est stationnaire. Un peu de trigonométrie peut maintenant être utilisée pour trouver les tensions. Une conclusion est possible d’emblée - nous pouvons voir à partir de la partie (b) de la figure que les amplitudes des tensions \(\vec{T}_{L}\) et \(\vec{T}_{R}\) doit être égal. En effet, il n’y a pas d’accélération horizontale dans la corde et les seules forces agissant à gauche et à droite sont \(\vec{T}_{L}\) et \(\vec{T}_{R}\). Ainsi, l’amplitude de ces forces doit être égale pour qu’elles s’annulent.

Chaque fois que nous avons des problèmes vectoriels bidimensionnels dans lesquels il n’y a pas deux vecteurs parallèles, la méthode la plus simple de solution consiste à choisir un système de coordonnées pratique et à projeter les vecteurs sur ses axes. Dans ce cas, le meilleur système de coordonnées a un axe horizontal et l’autre vertical. Nous appelons l’horizontale l’axe \(x\) et la verticale l’axe \(y\).

solution

Premièrement, nous devons résoudre les vecteurs de tension en leurs composantes horizontales et verticales. Il aide à dessiner un nouveau diagramme de corps libre montrant toutes les composantes horizontales et verticales de chaque force agissant sur le système.

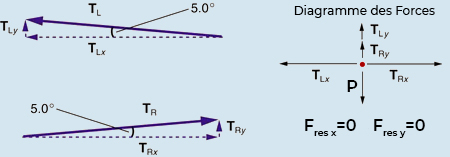
Fig. 9.15 Lorsque les vecteurs sont projetés sur des axes verticaux et horizontaux, leurs composantes le long de ces axes doivent s’additionner à zéro, puisque le funambule est stationnaire. Le petit angle entraîne \(\vec{T}\) étant beaucoup plus grand que \(\vec{P}\).

Considérons les composantes horizontales des forces (indiquées par un indice \(x\)) :

\[F_{res\,x}=T_{L\,x}-T_{R\,x}\]

La force horizontale extérieure résultante \(F_{res\,x}=0\), puisque la personne est stationnaire. Donc,

\[\begin{split}\begin{align*} F_{res\,x}=0& =T_{L\,x}-T_{R\,x}\\ T_{L\,x}& =T_{R\,x} \end{align*}\end{split}\]

Maintenant, observez la figure ci-dessus. Vous pouvez utiliser la trigonométrie pour déterminer l’ampleur de \(T_{L}\) et \(T_{R}\). Remarquerez que :

\[\begin{split}\begin{align*} \cos 5° & =\dfrac{T_{L\,x}}{T_{L}}\\ T_{L\,x} & =T_{L}\cos 5°\\ \\ \cos 5° & =\dfrac{T_{R\,x}}{T_{R}}\\ T_{R\,x} & =T_{R}\cos 5° \end{align*}\end{split}\]

et donc

\[T_{L}=T_{R}=T\]

comme prédit. Maintenant, en considérant les composantes verticales (désignées par un indice \(y\)), nous pouvons résoudre pour \(\vec{T}\). Encore une fois, puisque la personne est stationnaire, la deuxième loi de Newton implique que \(\vec{F}_{y}=0\). Ainsi, comme illustré dans le diagramme des forces de la figure ci-dessus,

\[F_{res\,y}=T_{L\,y}+T_{R\,y}-P\]

En observant la figure, nous pouvons utiliser la trigonométrie pour déterminer la relation entre \(T_{L\,y}\), \(T_{R\,y}\), et \(T\). Comme nous l’avons déterminé à partir de l’analyse dans la direction horizontale, \(T_{L}=T_{R}=T\) :

\[\begin{split}\begin{align*} \sin 5° & =\dfrac{T_{L\,y}}{T_{L}}\\ T_{L\,y} & =T_{L}\sin 5°=T\sin 5°\\ \\ \sin 5° & =\dfrac{T_{R\,y}}{T_{R}}\\ T_{R\,y} & =T_{R}\sin 5°=T\sin 5° \end{align*}\end{split}\]

Maintenant, nous pouvons remplacer les valeurs pour \(T_{L\,y}\) et \(T_{R\,y}\), dans l’équation de la force résultante dans la direction verticale :

\[\begin{split}\begin{align*} F_{res\,y}=T_{L\,y}+T_{R\,y}-P &=0\\ F_{res\,y}=T\sin 5°+T\sin 5°-P &=0\\ 2T\sin 5°-P & = 0\\ 2T\sin 5° & = P \end{align*}\end{split}\]

et

\[T=\dfrac{P}{2\cdot\sin 5°}=\dfrac{mg}{2\cdot\sin 5°}\]

et donc, la tension vaut

\[T=\dfrac{70\,kg\cdot 9.81\,m/s^{2}}{2\cdot\sin 5°}=3940\,N\]

discussion

Notez que la tension verticale du câble agit comme une force normale qui supporte le poids du funambule. La tension est presque six fois le poids de \(686\,N\) du funambule. Puisque le fil est presque horizontal, la composante verticale de sa tension n’est qu’une petite fraction de la tension dans le fil. Les grands composants horizontaux sont dans des directions opposées et s’annulent, de sorte que la plupart de la tension dans le fil n’est pas utilisée pour supporter le poids du funambule.

Si l’on souhaite créer une tension très importante, il suffit d’exercer une force perpendiculaire à un connecteur flexible, comme illustré sur la Fig. 9.16. Comme nous l’avons vu dans le dernier exemple, le poids du funambule agissait comme une force perpendiculaire à la corde. Nous avons vu que la tension dans la corde était liée au poids du funambule de la manière suivante :

\[T=\dfrac{P}{2\sin\theta}\]

On peut étendre cette expression pour décrire la tension \(\vec{T}\) créé lorsqu’une force perpendiculaire (\(\vec{F}_{\perp}\)) s’exerce au milieu d’un connecteur flexible :

\[T=\dfrac{F_{\perp}}{2\sin\theta}\]

Notez que \(\theta\) est l’angle entre l’horizontale et le connecteur plié. Dans ce cas, \(\vec{T}\) devient très grand lorsque \(\theta\) s’approche de zéro. Même le poids relativement faible de tout connecteur flexible le fera fléchir, car une tension infinie en résulterait s’il était horizontal (c.-à-d. \(\theta=0\) et \(\sin\theta=0\)). (Voir la Fig. 9.16.)

Fig. 9.16 On peut créer une très grande tension dans la chaîne en la poussant perpendiculairement à sa longueur, comme illustré. Supposons que nous souhaitons sortir une voiture de la boue lorsqu’aucune dépanneuse n’est disponible. Chaque fois que la voiture avance, la chaîne est tendue pour la maintenir aussi droite que possible. La tension dans la chaîne est donnée par \(T=\frac{P}{2\sin\theta}\); Vu que \(\theta\) est petit, \(\vec{T}\) est très grand. Cette situation est analogue à celle du funambule illustré à la figure de l’exemple précédent, sauf que les tensions indiquées ici sont celles transmises à la voiture et à l’arbre plutôt que celles agissant au point où \(\vec{F}_{\perp}\) est appliqué.

Fig. 9.17 À moins qu’une tension infinie ne soit exercée, tout connecteur flexible - comme la chaîne en bas de l’image - fléchira sous son propre poids, donnant une courbe caractéristique lorsque le poids est uniformément réparti sur la longueur. Les ponts suspendus, comme le Golden Gate Bridge illustré sur cette image, sont essentiellement des connecteurs flexibles très lourds. Le poids du pont est uniformément réparti sur la longueur des connecteurs flexibles, généralement des câbles, qui prennent la forme caractéristique. (crédit : Leaflet, Wikimedia Commons)

Force de frottement

TO DO…

Force d’Archimède

TO DO…

Sujet étendu: Forces réelles et cadres inertiels

Il existe une autre distinction entre les forces en plus des types déjà mentionnés. Certaines forces sont réelles, tandis que d’autres ne le sont pas. Les forces réelles sont celles qui ont une origine physique, comme l’attraction gravitationnelle. Par contraste, des forces fictives sont celles qui surviennent simplement parce qu’un observateur se trouve dans un cadre de référence en accélération, comme celui qui tourne (comme un manège) ou subit une accélération linéaire (comme une voiture qui ralentit). Par exemple, si un satellite se dirige plein nord au-dessus de l’hémisphère nord de la Terre, alors pour un observateur sur Terre, il semblera expérimenter une force à l’ouest qui n’a pas d’origine physique. Bien sûr, ce qui se passe ici, c’est que la Terre tourne vers l’est et se déplace vers l’est sous le satellite. Dans le cadre de la Terre, cela ressemble à une force vers l’ouest sur le satellite, ou cela peut être interprété comme une violation de la première loi de Newton (la loi d’inertie). Un cadre de référence inertiel est un cadre dans lequel toutes les forces sont réelles et, de manière équivalente, un cadre dans lequel les lois de Newton ont les formes simples données dans ce chapitre.

La rotation de la Terre est suffisamment lente pour que la Terre soit presque un cadre inertiel. Vous devez généralement effectuer des expériences précises pour observer les forces fictives et les légers écarts par rapport aux lois de Newton, comme l’effet que nous venons de décrire. À grande échelle, comme pour la rotation des systèmes météorologiques et des courants océaniques, les effets peuvent être facilement observés.

Le facteur crucial pour déterminer si un cadre de référence est inertiel est de savoir s’il accélère ou tourne par rapport à un cadre inertiel connu. Sauf indication contraire, tous les phénomènes discutés dans ce texte sont considérés dans des cadres inertiels.

Toutes les forces discutées dans cette section sont des forces réelles, mais il existe un certain nombre d’autres forces réelles, telles que la portance et la poussée, qui ne sont pas abordées dans cette section. Ils sont plus spécialisés et il n’est pas nécessaire de discuter de chaque type de force. Il est cependant naturel de se demander où se situe la simplicité fondamentale que nous cherchons à trouver en physique dans la longue liste des forces. Certains sont-ils plus basiques que d’autres? Y a-t-il des manifestations différentes de la même force sous-jacente ? La réponse aux deux questions est oui, comme on le verra dans d’autres chapitres.